Кэннон [42] предложил метод, позволяющий восстанавливать изображения лучше, чем с помощью винеровского или обратного фильтров; это так называемый метод уравнивания энергетических спектров или метод гомоморфной фильтрации. (Сначала такой фильтр был спроектирован Коулом [21] на основе теории гомоморфных систем, а затем Кэннон нашел эквивалентную форму, пользуясь методом уравнивания энергетических спектров, который и будет описан ниже.) Передаточная функция фильтра определяется из простого условия, гораздо более слабого, чем критерий минимума средней квадратической ошибки в винеровском фильтре. При проектировании фильтра отыскивается такая линейная оценка

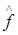 ( x, y ) = L [ g ( x, у )] ,

(где L - линейный оператор), чтобы энергетический спектр оценки равнялся энергетическому спектру исходного изображения. Таким образом, условие имеет вид :

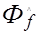                      ( u, v ) = 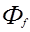( u, v ) .                       (4.47)

Поскольку g ( х, у ) определяется из соотношений (4.37) или (4.38), то энергетический спектр оценки 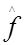 равен :

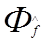( u, v ) = | L( u, v )|² [ | H ( u, v )|² Ф_f( u, v )+Ф_n( u, v )]. (4.48)

Его можно приравнять к правой части соотношения (4.47) и в явной форме найти |L ( u , v )| - модуль пространственно - частотной характеристики линейного фильтры, уравнивающего энергетические спектры (уэс). В результате характеристика фильтра будет иметь вид

 H_уэс( u, v ) = | L ( u, v ) | = [ 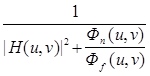  ] 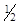,        (4.49)

а из соотношения

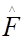                     ( u, v ) = Н_уэс ( u, v ) G ( u, v )                 (4.50)

определяются значения спектра восстановленного изображения. Для получения самого изображения эти значения нужно подвергнуть обратному преобразованию. Как ,и прежде, вычисления следует производить с применением БПФ.

Фильтр с уравниванием энергетических спектров обладает следующими свойствами:

1. При малых шумах, когда Ф_n 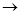 0, характеристика фильтра сводится к модулю характеристики обратного фильтра.

2. При малых сигналах, когда Ф_f 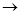 0, коэффициент передачи фильтра уменьшается до нуля.

3. В промежутке между этими экстремальными условиями коэффициент передачи фильтра больше, чем Н _w , но меньше, чем H_i . Это обусловлено отсутствием множителя Н* в числителе выражения для Н _w также свойствами операции извлечения квадратного корня. Можно показать, что характеристика фильтра с уравниванием энергетических спектров равна среднему геометрическому от характеристик винеровского и обратного фильтров [21].

Поскольку коэффициент передачи фильтры с уравниванием энергетических спектров больше, чем у винеровского фильтра, но не приводит к увеличению шумов, как в обратном фильтре, то восстановленное изображение содержит большее число мелких деталей, связанных с высокочастотными составляющими, которые винеровский фильтр обычно подавляет. При этом уровень шума увеличивается, но человек обычно согласен мириться с увеличением шума, если получает дополнительную полезную информацию о мелкой структуре изображения.

На рис. 4.15,а и б показаны изображения, исправленные фильтром с уравниванием энергетических спектров при условиях, соответствующих рис. 4.13, а и б. Снимки на рис. 4.13, a, 4.14, a и 4.15, а похожи; это указывает на то, что при слабых шумах этот фильтр имеет те же свойства, что и обратный. Результат восстановления изображения при сильном шуме представлен на рис. 4.15,6. Сравнение его с рис. 4.13,6, рис. 4.14,6 и с исходным изображением на рис. 4.12,а показывает преимущество данного метода повышения резкости изображений.

Соотношение (4.49) задает только модуль передаточной функции, но можно построить фильтры, в которых задается также определенная фазовая характеристика. Для многих видов искажений (например, для расфокусировки или смазывания изображений при движении) фазовая характеристика имеет значения 0 или ± 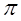 . Фильтр, описываемый соотношением (4.49), можно дополнить устройством, вносящим необходимый сдвиг фазы; в результате получается восстанавливающий фильтр, корректирующий в изображении как амплитудные, так и фазовые искажения. Кэннон [42] показал, что подобный метод повышения резкости лучше чисто амплитудной коррекции (как и следует из общих принципов).

Метод уравнивания энергетических спектров проясняет весьма важные особенности задачи восстановления «вслепую», т.е. путем оценивания параметров, необходимых для восстановления искаженного изображения по этому же искаженному изображению. При винеровской фильтрации необходимо заранее знать величины Ф _n , Ф _f и Н. Аналогичное требование можно сформулировать и для случая фильтрации методом уравнивания энергетических спектров. Однако внимательный анализ спектров, фигурирующих в соотношении (4.49), позволяет заметить, что оценки всех необходимых величин можно найти на основе искаженного изображения.

Рассмотрим изображение g ( x , y ), формируемое по законам, описываемым формулами (4.37) и (4.38) или им подобными. Разобьем изображение на части размером М 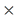М, где М велико по сравнению с размерами аппаратной функции, но мало по сравнению с размером исходного изображения N 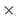N . Типичным значением является М=64. Отдельные части изображения могут перекрываться. Если пренебречь краевыми эффектами, то каждую часть изображения можно описать сверткой аппаратной функции с соответствующей областью полного первоначального распределения яркости объекта. Тогда соотношение

g_i ( x , у) 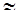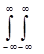h ( x - x ₁ , у— y ₁ ) f_i ( x ₁ , y ₁ ) dx ₁ dy ₁ + n_i ( x , y ) , (4.51)

аппроксимирует закон формирования изображения в каждой из частей g_i . После дискретизации g_i путем взятия М 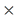М отсчетов можно найти энергетический спектр каждой части изображения, равный

Ф ⁱ _g ( u , v ) 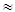| H ( u , v )|² Ф ⁱ _f ( u , v ) + Ф ⁱ _n ( u , v ) ,   (4.52)

где верхний индекс i обозначает номер части изображения. Если предположить, что изображение и шум можно аппроксимировать стационарными случайными процессами, то Фⁱ_f и Фⁱ_n будут выборками из двух функций, описывающих два энергетических спектра. Поэтому суммирование по i приведет к сглаживанию случайных отклонений в энергетических спектрах каждой из частей изображения. Таким образом,

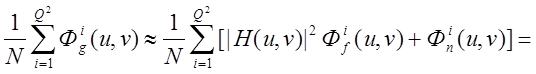
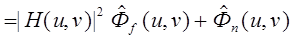       (4.53)

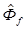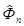где Q = N / M , а  и  —оценки энергетических спектров сигнала и шума соответственно.

Значение равенства (4.53) определяется следующими «соображениями:

1. Квадрат модуля преобразования Фурье от размытой аппаратной функции приводит к появлению характерных особенностей в усредненною энергетическом спектре частей изображения. Для таких видов искажений, как расфокусировка и смазывание при сдвиге, в спектре остаются характерные признаки, позволяющие установить тип искажения и определить все его существенные параметры, как, например, размер «размазанного» изображения точки и период обращений фазы [42].

2. Знаменатель 'передаточной функции фильтра с уравниванием энергетических спектров полностью совпадает с правой частью равенства (4.53), и если уже нам известна оценка Ф_f, то можно выполнять операцию восстановления изображения. Оценку Ф_f можно получить несколькими способами. Bo - первых, можно взять неискаженные изображения, подобные восстанавливаемому, и определить Ф_f но ним, так как было показано [21], что большинство изображений имеет очень похожие энергетические спектры. Или же можно на основе исправляемого изображения получить оценку Ф _n (обычно это удается сделать на однородных участках изображения), а также определить значения Н по его характерным признакам и решить уравнение (4.53) относительно .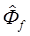

На pис. 4.16,а приведен снимок, сделанный камерой, двигавшейся в процессе съемки. Камера двигалась в горизонтальном направлении, и хорошо заметно, что из-за этого мелкие надписи стали совершенно неразличимыми. На рис. 4.16,6 показан тот же снимок после восстановления вышеописанным методом; смазывание за счет сдвига оставило в энергетическом спектре характерные признаки, которые были автоматически распознаны и применены при создании фильтра, восстанавливающего изображение методом уравнивания энергетических спектров. После восстановления текст стал вполне разборчивым. Дальнейшие сведения об этом методе восстановления изображений можно найти в работе [42].