Корпускулярно - хвильовий дуалізм речовини
1.1.1. Ядерна модель атома. Теорія Бора і її затруднення.
1.1.2. Гіпотеза і формула де Бройля. Дослідне обгрунтування
Корпускулярно - хвильового дуалізму речовини.
1.1.3. Співвідношення невизначеностей. Межі використання
Законів класичної фізики.
1.1.1. Ядерна модель атома. Теорія Бора і її затруднення
До кінця 19-го сторіччя атом вважали неподільним. Однак відкриття цілого ряду нових фізичних явищ поставили це ствердження під сумнів. На початку 20-го сторіччя було висунуто кілька моделей будови атома. При допомозі цих моделей вчені пробували пояснити ряд незрозумілих експериментальних фактів - лінійність спектрів випромінювання газів при високій температурі, електричну нейтральність і стійкість атомів.
Першу спробу побудувати теорію будови атома в межах класичної фізики зробив у 1903 р. англійський фізик Д.Томсон. За гіпотезою Томсона атом уявлявся у вигляді сфери, яка рівномірно заповнена позитивним зарядом, в середині якої містяться електрони. Проте ця модель була неспроможна пояснити спектральні закономірності атомів. За цією гіпотезою число ліній у спектрі не повинно було перевищувати число електронів в атомі, тоді як в дійсності навіть у спектрі атома водню число ліній перевищувало 30. Крім того гіпотеза Томсона не спиралась на будь які дослідні дані.
Вирішальне значення для теорії будови атома мали досліди Резерфорда, який у 1913 році вивчав розсіяння пучка a - частинок при проходженні їх через тонку металеву фольгу. Ці досліди показали, що при проходженні через фольгу переважна більшість a- частинок зазнає дуже незначних відхилень, але знаходиться чимале число і таких частинок, які зазнають дуже великих відхилень на кут, більший 150°. Таке значне розсіяння a- частинок могло статися тільки під дією позитивного заряду атома. Електрони, маса яких майже у 8000 разів менша від a - частинки, не могли помітно вплинути на її рух. Проходження переважної більшості a- частинок вказували на те, що розміри позитивного заряду атома повинні бути значно меншими від розмірів атома. Знаючи заряд атома q = Ze можна було визначити для різних кутів розсіювання так звані прицільні відстані a - частинок від центрів атомів. Виявилося, що для золотої фольги для кутів розсіювання 150° прицільна відстань дорівнює 10-14м. Якщо на такій відстані a- частинка і атом не взаємодіють, то це може означати лише одне - розміри позитивно зарядженої частини атома не перевищують 10-15м.
Ці дослідні факти дали можливість Резерфорду описати ядерну модель атома: в центрі атома міститься позитивно заряджене ядро атома, розміри якого мають величину порядку 10-15м, навколо ядра по замкнутих орбітах в об’ємі сфери радіусом порядку 10-10м обертаються електрони, причому їх кількість дорівнює порядковому номеру елемента.
В такому вигляді ядерна модель атома зберегла своє значення і до нашого часу, хоч і зазнала багатьох уточнень.
На кожний рухомий електрон в атомі діє доцентрова сила ядра, яка дорівнює кулонівській силі притягання електрона до ядра. Ця сила забезпечує стійкий орбітальний рух електрона в атомі, подібно орбітальному руху планет в сонячній системі.
Однак планетарна модель атома незабаром виявилась неприйнятною. Дійсно, електрони рухаючись в атомі з доцентровими прискореннями, згідно теорії Максвелла повинні випромінювати енергію у вигляді електромагнітних хвиль, що робить атоми не стійкими. Насправді атоми досить стійкі і при невисоких температурах енергії не випромінюють і не поглинають. В той же час при високих температурах будь-які атоми, перебуваючи у газоподібному стані, випромінюють електромагнітні хвилі у вигляді лінійчатих спектрів.
Вихід із затруднень знайшов датський фізик Нільс Бор. В основу нової моделі атома була покладена планетарна модель Резерфорда. Бор висунув припущення, що рух електронів в атомі, випромінювання і поглинання атомами електромагнітних хвиль підпорядковуються не класичним законам, а квантовим.
Ці закони Бор сформулював у вигляді наступних постулатів:
1. Електрони, які рухаються в атомі на окремих стаціонарних рівнях, не випромінюють і не поглинають електромагнітних хвиль. В стаціонарних станах атома електрони рухаються вздовж колових орбіт, які мають дискретні значення моменту імпульсу.
m u rn= n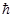 
, (1.1)
де m - маса електрона; u 
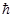- лінійна швидкість орбітального руху; rn - радіус n-ї колової орбіти; n - порядковий номер стаціонарного рівня - головне квантове число; - стала Планка поділена на 2 p ( 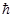= h / 2 p ).
2. При переході електрона з однієї стаціонарної орбіти на іншу випромінюється або поглинається квант енергії
hn = En2 - En1 , (1.2)
який дорівнює різниці енергій двох стаціонарних рівнів атома .
Зміст формули (1.2) має принципове значення. Він виражає два нових фундаментальних ствердження:
а) енергетичний c спектр атома дискретний;
б) частоти атомного випромінювання пов’язані з атомними рівнями.
Величезна заслуга Нільса Бора перед наукою полягає в тому, що він вперше усвідомив дискретність енергетичного спектра атома. Історичний дослід Франка і Герца був першою дослідною перевіркою цих передбачень.
Однак теорія Бора має ряд внутрішніх протиріч:
З одного боку в ній використовуються закони класичної фізики, а з іншого боку вона базується на квантових постулатах. Так результати теорії вивчення випромінювання атома водню і воднево подібних атомів блискуче співпали з експериментом. Теорія Бора також пояснила причину випромінювання лінійчатих спектрів складними атомами, періодичний закон Менделєєва і закон Мозлі. Однак залишалось не виясненим: Чому рух електронів в атомах підпорядкований двом постулатам Бора? Чому одні лінії спектра досить інтенсивні, а інші ні? Чому здійснюються лише певні переходи електронів в атомах при випромінюванні і поглинанні ними енергії?
Досить значним недоліком теорії Бора була неможливість описати з її допомогою будову атома гелію, наступного за атомом водню елемента.
Відповіді на поставлені запитання дала квантова механіка, в якій на принципово новій основі установлені закономірності руху електронів в атомах і будь-яких частинок в інших системах.
Законів класичної фізики
В класичній механіці траєкторія руху тіла характеризується точними значеннями координати x ( t ) і імпульсу p ( t ) в довільний момент часу t, причому ці два параметри зв’язані між собою. Наприклад, рівномірний і прямолінійний рух тіла масою m з швидкістю u виражається координатою х( t ) = u t і імпульсом p ( t )= m u , звідки одержуємо, що х( t )= p ( t ) t / m.
В мікросвіті частинки проявляють при одних умовах хвильові властивості, при інших умовах - корпускулярні. Якщо виходити лише з корпускулярних властивостей , то згідно теорії Н. Бора можна визначити точне значення координати частинки в просторі. У випадку хвильових властивостей елементарних частинок поняття координати хвилі немає фізичного змісту.
В квантовій фізиці з урахуванням хвильових властивостей частинок показано, що у частинки не існує одночасно точних значень координат і імпульсу і що ці величини між собою навіть не пов’язані. Якщо імпульс частинки має точне значення, то її місце знаходження невизначене і навпаки. Така закономірність мікросвіту відображена співвідношеннями невизначеностей Гейзенберга.
Розглянемо дифракцію електронів на одній щілині. Нехай пучок електронів з швидкістю u летить в напрямі осі OY так, як це показано на рис. 1.4.
 |
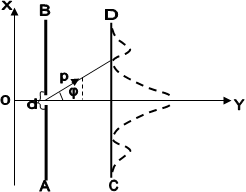Рис.1.4
Екран АВ з щілиною шириною d розміщено перпендикулярно до пучкаa. На другому екрані СД одержано розподіл інтенсивності, який співпадає з розподілом інтенсивності при дифракції світла від однієї щілини. На рис. 1.4 цей розподіл зображено пунктирною лінією. Максимум нульового порядку одержано при куті дифракції j, який задовольняє умові :
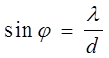, (1.12)
де l - довжина хвилі, яка відповідає пучку електронів.
З рис. 1.4 видно, що переважна більшість електронів формують нульовий максимум, тому вторинними максимумами в цьому випадку можна знехтувати. Якщо уявити електрони у вигляді механічних частинок, то можна стверджувати, що при їх русі з швидкістю u в напрямі осі OX їх положення визначається з точністю до ширини щілини, тобто
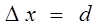. (1.13)
В той же час, внаслідок дифракції змінюється напрям швидкості частинок. Враховуючи лише ті електрони, які формують центральний максимум дифракції, похибку у визначенні проекції імпульсу на напрям осі OX знайдемо із умови
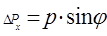. (1.14)
Тому
D х. D Рх ³ p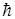 
, (1.50)
що перебуває у повній відповідності із співвідношенням невизначеностей імпульс - координата.
Покажемо, як залежить ширини енергетичного інтервалу D Е від розмірів потенціального ящика. У потенціальному ящику з розмірами l =10-9м. Власні значення енергії електрона утворюють послідовність енергетичних рівнів, енергетична відстань між якими дорівнює
D E=En+1-En.
Або
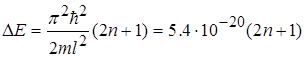Дж.
В електрон-вольтах ця енергія дорівнює
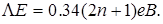
Коли ширина потенціального ящика співрозмірна з розмірами атома, енергетичний інтервал між сусідніми енергетичними рівнями досить значний, а спектр є дискретним.
У випадку, коли потенціальний ящик має мікроскопічні розміри l » 10-2м., енергетичний інтервал між сусідніми рівнями дорівнює
Дж=0,34.10-14(2n+1) eB.
Для такого потенціального ящика квантуванням енергії можна знехтувати. Вона нічим не відрізняються від значень енергії, одержаних класичними методами.
Аналогічні результати можна одержати для великих квантових чисел n. У цьому випадку проявляється принцип відносності, встановлений Бором у 1923р.
При великих квантових числах висновки і результати квантової механіки збігаються з відповідними класичними результатами.
1.3.3. Гармонічний квантовий осцилятор.
Просторово-обмеженим є також рух квантового осцилятора. З класичної точки зору осцилятором може бути будь-яка матеріальна точка, яка здійснює гармонічні коливання під дією квазіпружної сили.
F =- kx, де k = m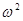 
(1.51)
Потенціальна енергія класичного осцилятора знаходиться за формулою
де m - маса частинки;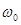 
- циклічна частота осцилятора.
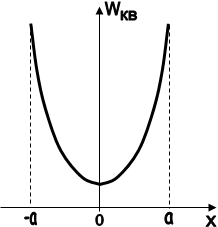Графічна залежність енергії класичного осцилятора показана на рис.1.8.
Рис. 1.8
.
З рисунка видно, що осцилятор може мати практично довільну енергію, навіть рівну нулю. В точках -а і +а кінетична енергія осцилятора дорівнює нулю, а потенціальна енергія досягає свого максимуму. За межі області (-а, +а) класичний осцилятор вийти не може.
Квантовим осцилятором може бути лише елементарна частинка, яка поряд з корпускулярними властивостями проявляє і хвильові властивості. Прикладом квантового осцилятора може бути коливний рух атомів і молекул у вузлах кристалічної гратки. Потенціальна енергія квантового осцилятора має таку ж математичну залежність, що і класичний осцилятор (1.52).
Стаціонарне рівняння Шредінгера для лінійного гармонічного осцилятора має вигляд:
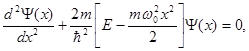(1.53)
де m - маса квантової частинки;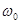 
- циклічна частота; Е - повна енергія частинки.
Знаходження хвильових функцій квантового осцилятора є досить складною математичною задачею. Тому, опускаючи такі розв’язки, наводимо енергетичний спектр квантового осцилятора. Він має вигляд
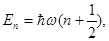(1.54)
де n = 0,1,2,3,..... - любе ціле число, починаючи з нуля;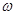 
- циклічна частота; 
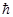- стала Дірака.
Аналіз рівняння (1.54) показує, що енергетичний спектр квантового осцилятора є дискретним і що власні значення енергії дорівнюють:
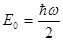
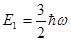
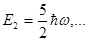
В енергетичному спектрі (1.54) проміжки між енергетичними рівнями не залежать від квантового числа n, а є однаковими
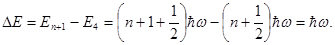(1.55)
Як показано на рис. 1.9, де енергетичний спектр квантового осцилятора суміщається з аналогічним спектром класичного осцилятора, квантовий осцилятор не має значень енергії, рівних нулю.
Найменше значення енергії квантового осцилятора дорівнює
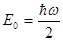(1.56)
Меншої енергії квантовий осцилятор не може мати навіть при абсолютному нулі температур.
Рис. 1.9
Покажемо наближеним способом, що енергія квантового осцилятора квантується. З рис 1.10 видно, що на відрізку l =2х0 вкладається ціле число півхвиль де Бройля, тобто
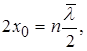(1.57)
 |
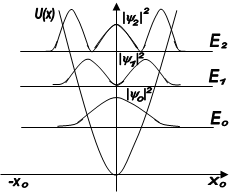Рис 1.10
де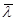 
- середнє значення довжини хвилі де Бройля.
Звідки
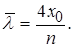(1.58)
Середнє значення імпульсу кванта хвилі де Бройля
(1.59)
Середня кінетична енергія такого осцилятора
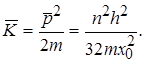(1.60)
Відомо, що повна енергія Е перевищує середнє значення кінетичної енергії в два рази, тобто
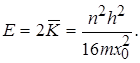(1.61)
З іншої точки зору повна енергія квантового осцилятора дорівнюватиме максимальній потенціальній енергії
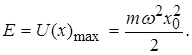(1.62)
Перемножимо рівності (1.61) і (1.62)
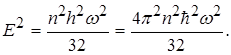(1.63)
Або
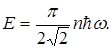(1.64)
В межах точності наших міркувань 
»1, тому
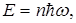(1.65)
де n =1,2,3,... - цілі числа.
Наближений розрахунок показує, що енергія квантового осцилятора набуває ряду дискретних значень, тобто квантується.
Точне значення енергії квантового осцилятора для не збудженого, нульового рівня можна одержати із рівняння Шредінгера (1.53), якщо згідно рис. (1.10) скористатись функцією Гаусса, яка дорівнює
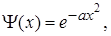(1.66)
де а - стала величина, яку слід визначити.
Другу похідну від (1.66) підставимо в (1.53)
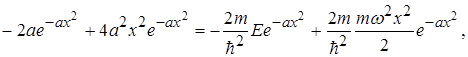
звідки
. (1.67)
Тотожність (1.67) має місце при рівності коефіцієнтів при х2 і вільних членів, тобто
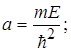
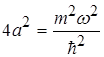(1.68)
Система рівнянь (1.68) дає значення енергії Е і сталої величини а
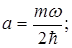
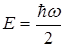(1.69)
Таким чином функція Гаусса є розв’язком рівняння Шредінгера (1.53) лише за умови, коли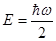 
.
В цьому випадку
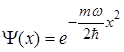. (1.70)
Слід відмітити, що так як відстань між суміжними рівнями енергії квантового осцилятора дорівнює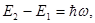 
то з урахуванням 
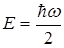одержуємо енергетичний спектр квантового осцилятора у вигляді
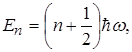(1.71)
де n = 0,1,2,3....
1.3.4.Проходження частинки крізь потенціальний бар’єр. Тунельний ефект.
Класична частинка не може перебувати в тих місцях, де її потенціальна енергія U ( x ) перевищувала б повну енергію частинки E. Щодо квантової частинки, то вона має таку властивість із-за того, що існує відмінна від нуля імовірність проникнення її крізь потенціальний бар’єр, тобто в область, де U ( x ) > E
Проведемо оцінку цієї імовірності шляхом розв’язування наступної задачі. Нехай квантова частинка з масою m, рухаючись в напрямі осі х, вдаряється в потенціальний бар’єр кінцевої висоти U 0, тобто
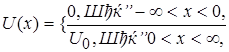
причому енергія частинки e менша висоти бар’єра U 0, (рис. 1.11).
Рис. 1.11
В області потенціального бар’єра рівняння Шредінгера для стаціонарних станів набуде вигляду
(1.72)
Якщо позначити вира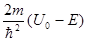з 
через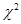 
, то рівняння (1.72) перепишеться
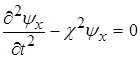. (1.73)
Розв’язком рівняння (1.34) може бути функція
, (1.74)
де А і В - деякі константи, і - уявна одиниця.
Експонента з додатним знаком фізичного змісту не має і може бути відкинута, так як не повинно бути зростання імовірності в області потенціального бар’єра. Тому в області потенціального бар’єра (х>0), хвильова функція частинки Y x визначається рівністю
Y x = Be-i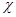 
x (1.75)
Коефіцієнт В у виразі (1.75) пов’язаний з інтенсивністю променя частинок, які рухаються в напрямі бар’єра, а тому задається довільно. Як правило х > 0 координати частинок розподіляються з густиною імовірності
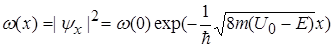, (1.76)
де w ( 0 ) дорівнює значенню |Y x|2 при х=0.
Рівняння (1.76) показує, що із збільшенням глибини проникнення в область потенціального бар’єра, густина імовірності w ( х ) зменшується експоненційно. Це зменшення буде тим швидше, чим більша різниця енергій U 0 - E .
Знайдемо глибину проникнення елементарної частинки в область потенціального бар’єра при умові, що m = 9,1 10-31кг (електрон), U 0 - E = 10-4 eB, а густина імовірності w (х ) на цій відстані зменшується в е разів
.
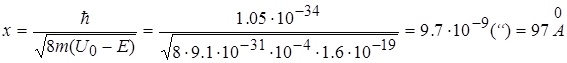Ця відстань перевищує на два порядки діаметр атома водню. Глибина проникнення зменшується на порядок, якщо різниця енергій U 0 - E зросте до 10-2 еВ.
Здатність квантових частинок проникати в область потенціального бар’єра приводить до тунельного ефекту. Його суть полягає в проникненні частинки із однієї області в іншу область, які поділені потенціальним бар’єром навіть в тих випадках, коли енергія частинки Е менше висоти потенціального бар’єра U 0.
Таке проходження частинки виявляється можливим дякуючи існуванню під бар’єром хвильової функції, яка «прокладає» шлях частинки на будь-яку відстань. Тунельний ефект є головною причиною a - розпаду радіоактивних ядер.
2. Фізика атомів і молекул
2.1. Атом водню
2.1.1. Використання рівняння Шредінгера до атома водню.
Правила відбору.
Знаючи кількісне співвідношення для енергії електрона на енергетичному рівні в атомі водню, можна розрахувати весь його спектр. Нехай енергія більш високого збудженого енергетичного рівня дорівнює
(2.1.19)
а енергія нижчого рівня
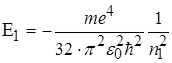(2.1.19)
Частоти, які відповідають різним спектральним лініям, можна записати у вигляді
,
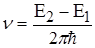або
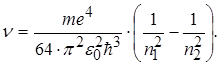(2.1.21)
Серія спектральних ліній, яким відповідає n 1 =1, називається серією Лаймана. Всі лінії цієї серії розміщені в ультрафіолетовій області спектра електромагнітного випромінювання. У випадку, коли n 1 =2, виникає друга серія випромінювання, яка називається серією Бальмера. Перші чотири лінії цієї серії знаходяться у видимій області спектра. Інші спектральні лінії цієї серії перебувають на межі видимої і ультрафіолетової області спектра.
Формула (2.1.21) називається формулою Бальмера. У цій формулі вираз перед дужками є сталою величиною, яку називають сталою Рідберга. Стала Рідберга R розрахована з великою точністю. Її величина дорівнює
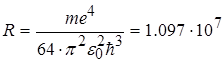м-1.
Число знаків, до яких визначена стала Рідберга показує рівень точності сучасної спектроскопії і ілюструє повне співпадання розрахунків за формулою Бальмера з результатами спостережень.
Якщо n 1 =3, то за формулою (2.1.21) можна розрахувати наступну серію випромінювання - серію Пашена. Всі лінії цієї серії перебувають в інфрачервоній області спектра.
Наступна серія випромінювання для n 1 =4 носить назву серії Бреккета. Лінії цієї серії перебувають в інфрачервоній області спектра.
Характер утворення спектральних серій атомом водню наведено на рис. 2.3.
Кожному значенню енергії електрона в атомі водню E n (за винятком Е1) відповідає декілька значень хвильової функції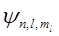 
. Вони відрізняються значеннями квантових чисел l i ml . Це означає, що атом водню може мати однакове значення енергії і перебувати в кількох різних квантових станах.
Стани з однаковою енергією називаються виродженими, а число таких станів з одним значенням енергії, називається порядком виродження.
Порядок виродження легко обчислити виходячи з числа можливих значень l i ml . Кожному значенню числа n відповідає 2 l +1 значень квантового числа ml. Тому число різноманітних станів для даного значення n, дорівнює
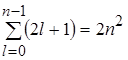(2.1.22)
Таким чином кожен рівень енергії атома водню має порядок виродження 2n 2 .
В квантовій механіці доводиться, що можливі лише такі переходи електронів між енергетичними рівнями, для яких виконується умова зміни орбітального квантового числа l на одиницю:
D l=±1 . (2.1.23)
Рис. 2.3.
Умова, яка виражена співвідношенням (2.1.23) називається правилом відбору. Існування цього правила обумовлено тим, що фотон має власний момент імпульсу, який називають спіном, рівним наближено 
. При випромінюванні фотон забирає від атома цей момент, а при поглинанні віддає атому. Тому правило відбору є відповідним наслідком закону збереження моменту імпульсу.
Переходи електронів в атомі водню, які дозволені правилом відбору показані на рис. 2.3.
Серії Лаймана відповідають переходи
np®1s, (n=2,3,4,...).
Серії Бальмера відповідають переходи
np®2s, ns®2p i nd®2p, (n=3,4,5,...).
Стан 1 s є основним станом атому водню. В цьому стані атом має найменшу енергію. Для виведення атома з основного стану йому слід надати необхідної енергії за рахунок зовнішнього джерела. Таким джерелом енергії може бути нагрівання, електричний розряд або опромінення.
При опромінені водню фотонами від зовнішнього джерела їх енергія поглинається повністю лише у випадку коли енергія фотонів в точності співпадає з різницею енергії двох енергетичних рівнів. В цьому випадку фотон зникає повністю, передаючи атому всю свою енергію. Атом не може поглинути частину фотона, так як фотон є неподільним.
2.1..3. Механічний і магнітний моменти атома водню.
Орбітальне квантове число l визначає стан електрона в атомі. Якщо рух електрона характеризується значенням квантового числа l =0, то електрон перебуває в s- стані, а сам електрон називається s-електроном. Квантовому числу l =1 відповідає р-стан електрона, l =2 - d-стан, l =3 - f-стан і т. д.
Для електрона, що знаходиться в атомі водню на n-му енергетичному рівні, можливі одна колова орбіта при l = n -1 i n -1 еліптичних орбіт. Із зменшенням l збільшується ступінь витягнутості орбіти. Отже, при заданому головному квантовому числі орбітальне квантове число l визначає форму орбіти.
У квантовій механіці орбітальний момент імпульсу електрона визначається таким співвідношенням:
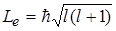, де (l=0,1,2,...n-1). (2.1.24)
Цей вираз свідчить про можливість таких рухів електрона, для яких (при l =0) орбітальний момент імпульсу електрона дорівнює нулю.
Третє квантове число ml , яке називається магнітним квантовим числом, визначає просторовий розподіл траєкторії руху електрона, а також і проекцію вектора механічного моменту або моменту імпульсу орбіти на заданий напрям.
Орбіту, по якій рухається електрон, можна розглядати як контур струму. Такий контур характеризується певним значенням орбітального магнітного моменту електрона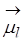 
, векторною величиною, що направлена вздовж осі орбіти в той бік, куди направлена індукція магнітного поля, створюваного цим контуром. Між вектором 
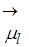і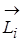 
існує наступний зв’язок
= - 
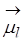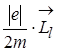=-g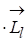 
, (2.1.25)
де е - заряд електрона; m - маса електрона; g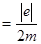 
- гіромагнітне відношення.
Враховуючи значення Ll з (2.1.24) одержимо:
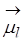=-g 
=- 
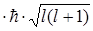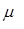б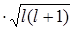 
, (2.1.26)
де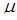 
б=g 
- магнетон Бора.
Як видно з (2.1.26) вектори 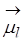і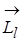 
мають протилежні напрямки.
Вектор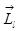 
може мати 2 l +1 просторових орієнтацій, а це означає, що при даному l електрон в атомі, який вміщено в зовнішнє магнітне поле, може рухатися по 2 l +1 орбітах, які відрізняються своєю орієнтацією щодо напрямку магнітного поля.
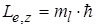, (2.1.27)
де ml - магнітне квантове число.
На рис. 2.4. зображено можливі значення проекції орбітального механічного моменту на напрям осі z зовнішнього магнітного поля для випадків l =1 i l =2.
Рис. 2.4.
Таким чином просторове квантування приводить до розчеплення в магнітному полі енергетичного рівня електрона на ряд підрівнів, а отже, і до розчеплення спектральних ліній. Таке явище спостерігав Зеєман. Розчеплення спектральних ліній також можливе в електричному полі - дослід Штарка.
Рис. 2.5
Між розщепленими рівнями можливі переходи електронів згідно правил відбору (рис. 2.5)
Dl=±1 i Dml=0 ; ±1.
2.2 Багатоелектронні атоми.
2.2.1. Досліди Штерна і Герлаха. Спін електрона.
2.2.2. Принцип нерозрізненості тотожних частинок. Принцип
Паулі.
2.2.3. Розподіл електронів за станами. Періодична система
Елементів.
2.2.4. Рентгенівські промені. Суцільний спектр і його межі.
Молекула
Парамагнітний резонанс.
Корпускулярно - хвильовий дуалізм речовини
1.1.1. Ядерна модель атома. Теорія Бора і її затруднення.
1.1.2. Гіпотеза і формула де Бройля. Дослідне обгрунтування
Дата: 2019-05-28, просмотров: 199.
