Теорія Бора будови і властивостей енергетичних рівнів електронів у воднево подібних системах знайшла своє підтвердження в квантовій механіці. Квантова механіка також стверджує, що:
a) електрони в атомах водню знаходяться лише в дискретних енергетичних станах. При переході електронів із одних станів в інші випромінюється або поглинається фотон;
б).не існує певних колових орбіт електронів. В силу хвильової природи електрони «розмиті» в просторі подібно до хмарки негативного заряду. Розміри і форму такої хмарки в заданому стані можна розрахувати.
Розглянемо рух електрона в кулонівському полі ядра з зарядом Ze, потенціальна енергія якого виражається формулою
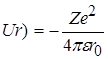, (2.1.1)
де r - відстань між електроном і ядром.
Стан електрона в атомі водню або воднево подібному атомі описується деякою хвильовою функцією Y, яка задовольняє стаціонарному рівнянню Шредінгера:
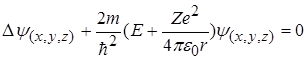, (2.1.2)
де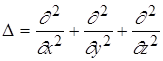 
- оператор Лапласа; Е - значення повної енергії електрона в атомі; m - маса частинки; 
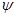( x , y , z ) - хвильова функція в декартові системі координат.
Для розв’язування рівняння Шредінгера (2.1.2), тобто знаходження виду хвильової функції для електрона в атомі водню слід перейти від декартових координат до сферичних. В цьому випадку зв’язок між параметрами цих систем координат визначається з рис.2.1.
Рис.2.1.
Співвідношення, які зв’язують координати x,y,z декартової прямокутної системи координат з сферичними координатами r , q , j наступні:
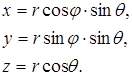(2.1.3)
Таким чином можна вважати, що хвильова функція y електрона в атомі водню залежить від сферичних координат, тобто y = y ( r , q , j ).
Опустивши не складні, але досить громіздкі перетворення переходу від декартової системи координат до сферичної, одержимо:
.
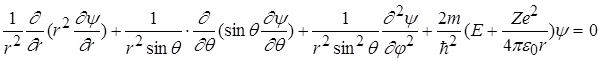(2.1.4)
Якщо розглядати основний (не збуджений) стан атома водню, то другою і третьою складовими в рівнянні (2.1.4) можна знехтувати. Електрон в такому стані рухається лише по коловій траєкторії, і хвильова функція не залежить від q і j. Тому
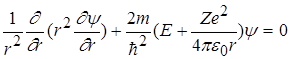. (2.1.5)
Хвильова функція y електрона в основному стані (2.1.5) є функцією лише r, тобто y = y ( r ). Такий стан називається s-станом; він має сферично-симетричний характер. Імовірність виявити електрон у заданій точці атома - залежатиме лише від r. Умовам стаціонарного стану відповідає легко диференціруєма центральносиметрична функція, яка має вигляд:
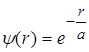, (2.1.6)
де a - деяка стала величина, яка має розмірність довжини.
Необхідні похідні від (2.1.6) підставимо в (2.1.5). Після скорочення на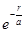 
одержимо:
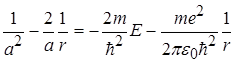. (2.1.7)
Рівність (2.1.7) має місце для будь-яких значень r при виконанні наступних умов:
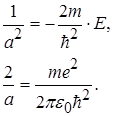(2.1.8)
З рівностей (2.1.8) одержуємо
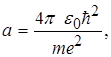(2.1.9)
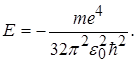(2.1.10)
Покажемо, що вираз (2.1.9) є найбільш імовірною відстанню електрона в атомі водню до ядра. Імовірність знайти електрон на відставні r від ядра, точніше в інтервалі відстаней від r до r + dr, тобто в кульковому шарі з об¢ємом dV =4 p r 2 dr, дорівнює:
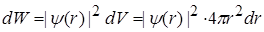. (2.1.11)
З урахуванням (2.1.6), хвильової функції основного стану маємо:
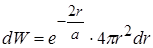, (2.1.12)
де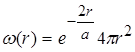 
- густина імовірності.
Дослідимо вираз (2.1.12) на максимум, тобто похідну від w(r) прирівняємо до нуля
.
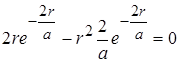Звідки
r = a. (2.1.13)
Цей результат є окремим випадком загального висновку: борівські орбіти електрона в атомі водню є геометричними місцями точок, в яких з найбільшою імовірністю можна виявити електрон.
Залежність густини імовірності w ( r ) виявити електрон на різних відстанях від ядра показана на рис.2.2.
Рис.2.2.
За теорією Бора імовірність виявити електрон у стані з n =1 відмінна від нуля лише для r = a, а згідно з висновками квантової механіки ця відстань є лише найбільш імовірною.
Теорія Бора дає можливість визначити значення енергії електрона в будь-якому енергетичному стані, а також радіус відповідних борівських орбіт:
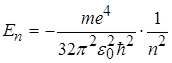, (2.1.14)
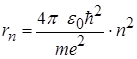, (2.1.15)
де m - маса електрона; e - заряд електрона; e 0 - діелектрична проникність вакууму;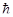 
- стала Планка, поділена на 2 p ; n =1,2,3... - головні квантові числа.
Співставлення (2.1.9) і (2.1.14), а також (2.1.9) і (2.1.15) показують, що висновки квантової механіки і теорії Бора повністю співпадають. Це співподання підкреслює значну історичну роль теорії Бора, яка ще не є квантовою, однак і не класичною теорією.
Хвильові функції для наступних двох енергетичних рівнів електронів в атомі водню мають вигляд
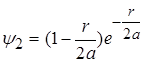, (2.1.16)
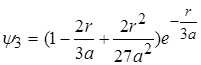. (2.1.17)
Ці хвильові функції також є розв¢язками рівняння (2.1.4) при умові, що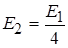 
і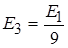 
. Можна показати, що формула (2.1.14) є значенням енергії електрона на будь-якому енергетичному рівні.
Однак для повного пояснення стану електрона в атомі водню необхідні ще два квантові числа, які входять у відповідні рівняння хвильових функцій і які характеризують момент імпульсу електрона в атомі.
Для збуджених атомів хвильові функції не є центрально симетричними і залежать не лише від r, а і від q і j. Ці хвильові функції містять три цілочислові параметри, які називають квантовими числами. Серед них:
n - головне квантове число, співпадає з аналогічним квантовим числом теорії Бора і набуває значень від 1 до ¥;
l - орбітальне квантове число, квантує момент імпульсу
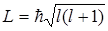. (2.1.18)
Орбітальне квантове число набуває значень l =0,1,2,... .
ml - магнітне квантове число, квантує проекцію орбітального моменту імпульсу на вісь Z напрямку зовнішнього магнітного поля
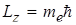. (2.1.19)
Магнітне квантове число набуває значень ml = 0, ± 1, ± 2 ,± 3... .
2.1.2. Енергія атома водню і його спектр. Виродження рівнів.
Правила відбору.
Знаючи кількісне співвідношення для енергії електрона на енергетичному рівні в атомі водню, можна розрахувати весь його спектр. Нехай енергія більш високого збудженого енергетичного рівня дорівнює
(2.1.19)
а енергія нижчого рівня
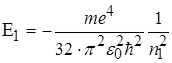(2.1.19)
Частоти, які відповідають різним спектральним лініям, можна записати у вигляді
,
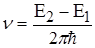або
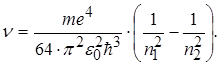(2.1.21)
Серія спектральних ліній, яким відповідає n 1 =1, називається серією Лаймана. Всі лінії цієї серії розміщені в ультрафіолетовій області спектра електромагнітного випромінювання. У випадку, коли n 1 =2, виникає друга серія випромінювання, яка називається серією Бальмера. Перші чотири лінії цієї серії знаходяться у видимій області спектра. Інші спектральні лінії цієї серії перебувають на межі видимої і ультрафіолетової області спектра.
Формула (2.1.21) називається формулою Бальмера. У цій формулі вираз перед дужками є сталою величиною, яку називають сталою Рідберга. Стала Рідберга R розрахована з великою точністю. Її величина дорівнює
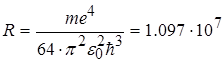м-1.
Число знаків, до яких визначена стала Рідберга показує рівень точності сучасної спектроскопії і ілюструє повне співпадання розрахунків за формулою Бальмера з результатами спостережень.
Якщо n 1 =3, то за формулою (2.1.21) можна розрахувати наступну серію випромінювання - серію Пашена. Всі лінії цієї серії перебувають в інфрачервоній області спектра.
Наступна серія випромінювання для n 1 =4 носить назву серії Бреккета. Лінії цієї серії перебувають в інфрачервоній області спектра.
Характер утворення спектральних серій атомом водню наведено на рис. 2.3.
Кожному значенню енергії електрона в атомі водню E n (за винятком Е1) відповідає декілька значень хвильової функції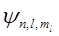 
. Вони відрізняються значеннями квантових чисел l i ml . Це означає, що атом водню може мати однакове значення енергії і перебувати в кількох різних квантових станах.
Стани з однаковою енергією називаються виродженими, а число таких станів з одним значенням енергії, називається порядком виродження.
Порядок виродження легко обчислити виходячи з числа можливих значень l i ml . Кожному значенню числа n відповідає 2 l +1 значень квантового числа ml. Тому число різноманітних станів для даного значення n, дорівнює
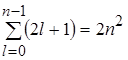(2.1.22)
Таким чином кожен рівень енергії атома водню має порядок виродження 2n 2 .
В квантовій механіці доводиться, що можливі лише такі переходи електронів між енергетичними рівнями, для яких виконується умова зміни орбітального квантового числа l на одиницю:
D l=±1 . (2.1.23)
Рис. 2.3.
Умова, яка виражена співвідношенням (2.1.23) називається правилом відбору. Існування цього правила обумовлено тим, що фотон має власний момент імпульсу, який називають спіном, рівним наближено 
. При випромінюванні фотон забирає від атома цей момент, а при поглинанні віддає атому. Тому правило відбору є відповідним наслідком закону збереження моменту імпульсу.
Переходи електронів в атомі водню, які дозволені правилом відбору показані на рис. 2.3.
Серії Лаймана відповідають переходи
np®1s, (n=2,3,4,...).
Серії Бальмера відповідають переходи
np®2s, ns®2p i nd®2p, (n=3,4,5,...).
Стан 1 s є основним станом атому водню. В цьому стані атом має найменшу енергію. Для виведення атома з основного стану йому слід надати необхідної енергії за рахунок зовнішнього джерела. Таким джерелом енергії може бути нагрівання, електричний розряд або опромінення.
При опромінені водню фотонами від зовнішнього джерела їх енергія поглинається повністю лише у випадку коли енергія фотонів в точності співпадає з різницею енергії двох енергетичних рівнів. В цьому випадку фотон зникає повністю, передаючи атому всю свою енергію. Атом не може поглинути частину фотона, так як фотон є неподільним.
2.1..3. Механічний і магнітний моменти атома водню.
Орбітальне квантове число l визначає стан електрона в атомі. Якщо рух електрона характеризується значенням квантового числа l =0, то електрон перебуває в s- стані, а сам електрон називається s-електроном. Квантовому числу l =1 відповідає р-стан електрона, l =2 - d-стан, l =3 - f-стан і т. д.
Для електрона, що знаходиться в атомі водню на n-му енергетичному рівні, можливі одна колова орбіта при l = n -1 i n -1 еліптичних орбіт. Із зменшенням l збільшується ступінь витягнутості орбіти. Отже, при заданому головному квантовому числі орбітальне квантове число l визначає форму орбіти.
У квантовій механіці орбітальний момент імпульсу електрона визначається таким співвідношенням:
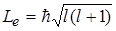, де (l=0,1,2,...n-1). (2.1.24)
Цей вираз свідчить про можливість таких рухів електрона, для яких (при l =0) орбітальний момент імпульсу електрона дорівнює нулю.
Третє квантове число ml , яке називається магнітним квантовим числом, визначає просторовий розподіл траєкторії руху електрона, а також і проекцію вектора механічного моменту або моменту імпульсу орбіти на заданий напрям.
Орбіту, по якій рухається електрон, можна розглядати як контур струму. Такий контур характеризується певним значенням орбітального магнітного моменту електрона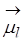 
, векторною величиною, що направлена вздовж осі орбіти в той бік, куди направлена індукція магнітного поля, створюваного цим контуром. Між вектором 
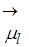і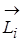 
існує наступний зв’язок
= - 
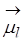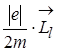=-g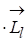 
, (2.1.25)
де е - заряд електрона; m - маса електрона; g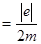 
- гіромагнітне відношення.
Враховуючи значення Ll з (2.1.24) одержимо:
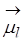=-g 
=- 
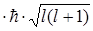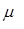б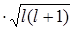 
, (2.1.26)
де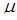 
б=g 
- магнетон Бора.
Як видно з (2.1.26) вектори 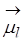і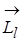 
мають протилежні напрямки.
Вектор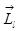 
може мати 2 l +1 просторових орієнтацій, а це означає, що при даному l електрон в атомі, який вміщено в зовнішнє магнітне поле, може рухатися по 2 l +1 орбітах, які відрізняються своєю орієнтацією щодо напрямку магнітного поля.
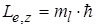, (2.1.27)
де ml - магнітне квантове число.
На рис. 2.4. зображено можливі значення проекції орбітального механічного моменту на напрям осі z зовнішнього магнітного поля для випадків l =1 i l =2.
Рис. 2.4.
Таким чином просторове квантування приводить до розчеплення в магнітному полі енергетичного рівня електрона на ряд підрівнів, а отже, і до розчеплення спектральних ліній. Таке явище спостерігав Зеєман. Розчеплення спектральних ліній також можливе в електричному полі - дослід Штарка.
Рис. 2.5
Між розщепленими рівнями можливі переходи електронів згідно правил відбору (рис. 2.5)
Dl=±1 i Dml=0 ; ±1.
2.2 Багатоелектронні атоми.
2.2.1. Досліди Штерна і Герлаха. Спін електрона.
2.2.2. Принцип нерозрізненості тотожних частинок. Принцип
Паулі.
2.2.3. Розподіл електронів за станами. Періодична система
Елементів.
2.2.4. Рентгенівські промені. Суцільний спектр і його межі.
Дата: 2019-05-28, просмотров: 285.
