2.2.1. Досліди Штерна і Герлаха. Cпін електрона

Висновки квантової механіки про просторове квантування потребували експериментального підтвердження . Виявилось, що всі електронні лінії мають так звану «тонку структуру», яка спостерігається навіть при відсутності зовнішнього магнітного поля. Так, всі спектральні лінії водню і лужних металів є дублетами, тобто складаються з двох окремих, близько розташованих ліній. Була висунута гіпотеза про наявність у електронів власного механічного моменту, пов’язаного з обертанням його навколо власної осі. Пізніше власний механічний момент електронів S назвали спіном. Чисельно спін електрона дорівнює 1/2 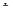. Електрону властивий також магнітний момент, що дорівнює магнетону Бора m _Б = 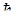g, де g - гіромагнітне відношення, рівне e /2 m; Власний механічний і магнітний моменти електрона можуть бути орієнтовані лише двома способами: паралельно або антипаралельно відносно вибраного напрямку. Ці дві орієнтації визначаються четвертим квантовим числом, яке називається спіновим. Спінове квантове число може набувати значень 1/2 і -1/2 . Отже, на ряду з уже введеними раніше трьома квантовими числами n, l, m_l  є ще четверте квантове число m_s - яке квантує власний механічний момент електрона.

Гіпотезу про існування власного механічного моменту (спіну) і власного магнітного моменту було пояснено в дослідах Штерна і Герлаха, виконаних ними ще в 1921-1923р.р.

Для дослідження були використані нейтральні атоми срібла, на зовнішніх оболонках яких рухається по одному електрону. Схема установки дослідів Штерна і Герлаха показана на рис. 2.6.

                               Рис. 2.6

 В установці на рис. 2.6. було створено досить неоднорідне магнітне поле за рахунок особливої конструкції магнітних полюсів постійного магніту.

Потенціальна енергія атомів срібла пов’язана з Р_м і В співвідношенням

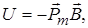                                                           (2.1.28)

де 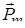  - вектор магнітного моменту атому срібла:

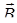- вектор індукції зовнішнього магнітного поля.

 Якщо зовнішнє магнітне поле буде постійним, то магнітні моменти атомів срібла, здійснювали б прецесію навколо вектора 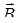, а магнітні сили були б відсутні.

В сильно неоднорідному магнітному полі цього не спостерігається, так як

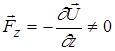, тому що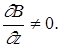

Отже

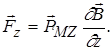                                                            (2.1.29)

Під дією цієї магнітної сили (2.1.29.) повинно бути розчеплення спектральних рівнів.

Якщо просторового квантування немає, тобто орієнтація магнітних моментів атомів у зовнішньому магнітному полі довільна, то на екрані спостерігатиметься неперервний розподіл атомів. При просторовому квантуванні пучок атомів після проходження неоднорідного поля розчеплюється на кілька пучків. Таке розчеплення атомних пучків спостерігали Штерн і Герлах і тим самим довели справедливість положення про просторове квантування магнітних моментів атомів. Проте виявилося, що в окремих дослідах є розбіжність між результатами експерименту і вимогами теорії.

Так, в експерименті з атомами срібла спостерігалось розчеплення пучка атомів, що проходили неоднорідне магнітне поле на два пучки, тоді як за теорією ці атоми не повинні зазнавати дії магнітного поля, оскільки їх орбітальні магнітні моменти в основному стані дорівнюють нулю.

Аномальне розчеплення атомних пучків водню, літію, срібла на два пучки неоднорідним магнітним полем  пов’язане з квантуванням власного магнітного моменту атомів.

            (2.1.30)

де m_s - спінове квантове число, рівне 1/2 і -1/2.

В дослідах Штерна і Герлаха було встановлено, що власний магнітний момент електронів дорівнює

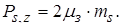                                                           (2.1.31)   

Спінове гіромагнітне відношення в два рази перевищує орбітальне. Наявність власного механічного моменту електрона заборонена теорією відносності. Це говорить про те, що класичної інтерпретації власний механічний момент немає.

З квантової точки зору цю властивість частинок називають спіном, і інтерпретують як невід’ємну властивість елементарних частинок.

Спін та власний магнітний момент мають протони, нейтрони та інші елементарні частинки.

2.2.2. Принцип нерозрізненості тотожних частинок. Принцип Паулі

До цих пір ми розглядали рух лише однієї квантової частинки. Незвичайні, з класичної точки зору властивості, проявляються при вивченні руху системи квантових частинок. Квантова теорія систем частинок полягає в тому, що в цій теорії поняття хвильової функції відноситься лише до системи частинок. Кожна окрема частинка системи не знаходиться в певному квантовому стані і не може бути охарактеризована своєю хвильовою функцією, яка б залежала лише від параметрів даної частинки.

Система квантових частинок набуває властивостей, яким не має аналога ні в класичній фізиці ні в квантовій механіці однієї частинки. Специфічна особливість квантової теорії систем частинок полягає в їх принциповій нерозрізненості. Всі частинки такої квантової системи є тотожними.

Нерозрізненість тотожних частинок в квантових системах не властива для систем класичних частинок, де кожна частинка системи має свою індивідуальність.

В квантовій фізиці однакові частинки втрачають свою індивідуальність, так як рухаються не по траєкторіях. Поняття траєкторії квантових частинок із за хвильових властивостей втрачає будь-який фізичний зміст.

Із принципової нерозрізненості однакових частинок випливає, що перестановка місцями двох однакових частинок в системі не впливає ні на одну із фізичних величин, що характеризують цю систему.

Слід відмітити, що при перестановці місцями двох частинок в системі хвильова функція, яка є функцією всіх параметрів частинок цієї системи, змінюється з Y на Y ¹ . Однак густина імовірності при цьому не змінюється, тобто

|Y |²=|Y ¹ |².

В той же час хвильова функція Y ¹ відрізняється від Y на множник e^{i a} , де a - деяка дійсна величина. Переставимо ті ж частинки ще раз місцями, тобто повернемось в попередній стан. Густина імовірностей знову ж не зміниться, а от хвильова функція Y буде відрізнятись від Y в початковий момент на е^{2і a} . Для рівності імовірностей необхідно, щоб  е^{2і a} =1, а е^{і a} = ± 1. З цих міркувань видно, що при перестановці місцями довільної пари частинок системи хвильова функція може залишитися такою ж, або змінювати знак.

Хвильова функція, яка при перестановці місцями двох частинок системи свого знаку не змінює - називається симетричною. В тих випадках, коли при аналогічній перестановці частинок системи хвильова функція змінює знак, вона є антисиметричною.

Симетрія хвильової функції системи однакових частинок зберігається з часом. Тому тип симетрії хвильової функції є властивістю тільки самих частинок.

Системи однакових частинок з нульовими, або цілочисловими спінами описуються лише симетричними хвильовими функціями і називаються бозонами.

Системи однакових частинок з напівцілими спінами описуються лише антисиметричними хвильовими функціями і називаються ферміонами.

До ферміонів відносяться електрони ( 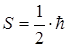), протони і нейтрони ( 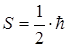) й інші частинки.

До бозонів відносяться p - мезони ( ), фотони ( ) і інші частинки.

Спін мікроскопічної частинки є її найважливішою характеристикою. Так від спінів частинок залежать статистичні властивості квантових систем, які складаються з багатьох частинок. Статистичні властивості частинок з нульовими і цілочисловими спінами вперше вивчали Бозе й Ейнштейн ще в 1924 році, від чого відповідна квантова статистика дістала назву статистики Бозе і Ейнштейна. Статистичні властивості частинок з напівцілими спінами вивчали в 1926 році Фермі і Дірак - звідки назва відповідної квантової статистики Фермі і Дірака.

Зупинимось на розподілі електронів в атомі на відповідних енергетичних рівнях. Відомо, що стан кожного із електронів можна характеризувати чотирма квантовими числами: n , l , m_l , m_s, де n - головне квантове число, яке квантує енергію електрона в атомі і визначає розміри орбіти електрона; l - орбітальне квантове число, що визначає (квантує) орбітальний момент імпульсу (механічний момент); m_l - магнітне квантове число, квантує проекцію вектора механічного моменту на заданий напрям зовнішнього магнітного поля; m_s - спінове квантове число, що визначає орієнтацію власного механічного і магнітного моментів електрона.

За принципом Паулі (1924 р.) електрони, які входять до складу якої-небудь системи, зокрема електрони атомних оболонок, не можуть перебувати в тотожних станах руху. Інакше кажучи, в будь-якому стаціонарному стані, що характеризується сукупністю чотирьох квантових чисел n,l,m_l, m_s, не може перебувати більше одного електрона.

Принцип Паулі має використання лише для систем, частинок з антисиметричними хвильовими функціями, тобто до ферміонів.

2.2.3. Розподіл електронів за станами.