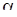Использованный в предыдущем разделе метод моментов приводит, при определенных условиях, к состоятельным оценкам. Однако оценки по методу моментов, вообще говоря, неэффективны. К тому же метод моментов неприменим, когда теоретические моменты нужного порядка не существуют. Одним из популярных общих методов получения оценок параметров, обладающих рядом преимуществ по сравнению с методом моментов, является метод максимального правдоподобия (м.м.п.).Напомним суть этого метода.
Пусть имеем вектор наблюдений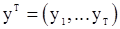 
случайной последовательности 
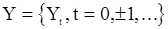и 
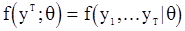- совместная плотность этих наблюдений. Векторный параметр 
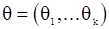принадлежит параметрическому множеству 
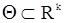. Функция правдоподобия (при фиксированных наблюдениях) определяется как следующая функция параметра 
:
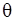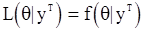. (93)
Принцип максимального правдоподобия (м.п.) предписывает выбор в качестве оценки параметра 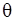такого значения 
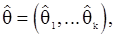для которого
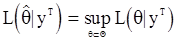. (94)
Верхняя грань может не достигаться, и для таких случаев вводится модифицированная оценка м.п.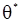 
, определяемая условием
,
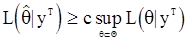где c - фиксированное число,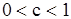 
. Может случится, что для некоторых наблюдени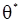й 
и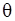 
не существуют. Однако можно показать, что при условиях регулярности на 
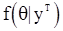такими наблюдениями можно пренебречь.
Часто удобно работать не с функцией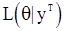 
, а с ее логарифмом: 
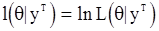. Условие (94) переходит в
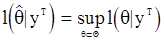. (95)
Если супремум в (95) достигается во внутренней точке множества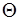 
и 
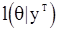дифференцируема по 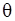, то в точке 
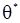дожны обращатся в нуль частные производные функции 
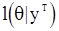. Следовательно, в этом случае 
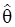удовлетворяет уравнениям
, 
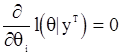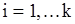. (96)
Уравнения (96) называются уравнениями м.п., а всякое их решение - оценкой м.п. Оценку, определяемую условием (95), называют оценкой метода м.п.
Общие свойства оценок м.п. по независимым наблюдениям можно найти, например, в [7]. Нас же будут интересовать оценки м.п. параметров по зависимым наблюдениям, а именно, по с.п. АР(p), СС(q) и АРСС(p,q). Для получения оценок м.п., согластно вышесказанному, нужно прежде всего найти функцию правдоподобия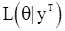 
. Однако, удобные для использования формулы для 
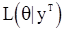удается получить только в предположении, что входная последовательность 
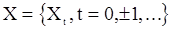- гауссовская. Тогда в силу линейности преобразований, осуществляемые формулами (7), (32) и (43), выходная последовательность 
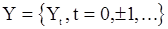тоже будет гауссовской. Если 
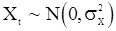и обеспечена стационарность последовательности Y, то вектор 
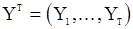будет гауссовским с нулевым вектором средних значений и корреляционной матрицей 
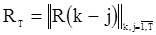, где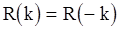 
находятся по формулам (33) для последовательности СС(q) и из уравнений (11) и (46) дял последовательностей АР(p) и АРСС(p,q) соответственно. Следовательно, плотность вектора 
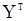будет иметь вид
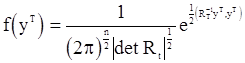, (97)
где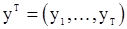 
, 
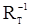- матрица, обратная к корреляционной, символ 
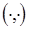обозначает скалярное произведение в эвклидовом пространстве размерности T. Практическому использованию плотности (9) при больших T препятствуют трудности обращению матрицы R. Однако м.м.п. удается реализовать для конкретных моделей гауссовских случайных последовательностей, к рассмотрению которых мы и перейдем.
М.м.п. для с.п. АР( p ). В соответствии с идеей м.м.п. начнем с рассмотрения функции правдоподобия. Предположим, что на вход авторегрессионной модели (7) подается гауссовский «шум»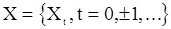 
с 
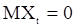и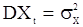 
. Так как модель (7) осуществляет линейное преобразование, то выходной «сигнал» 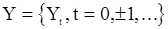, как известно, тоже будет гауссовским. Если модель (7) стационарна, то с.п. Y стационарна 
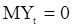и корреляционной функцией, определяемой разностным уравнением вида (11). Для гауссовского вектора 
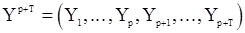плотность распределения может быть записана в соответствии с формулой (97)
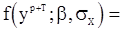
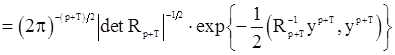, (98)
где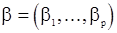 
-вектор параметров модели (7), 
, 
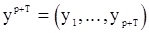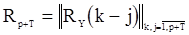- корреляционная матрица вектора 
.
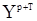При использовании плотности (98) можно избежать обращения матрицы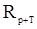 
. Для этого воспользуемся представлением
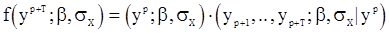, (99)
где первый множитель правой части - безусловная плотность вектора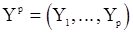 
, получающаяся из (98) при 
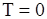, а второй - условная плотность вектора 
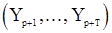при фиксированном значении вектора 
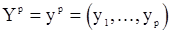. Эту условную плотность можно получить, используя плотность распределения вектора 
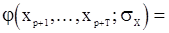
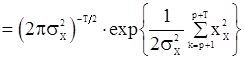, (100)
Но при фиксированном векторе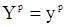 
вектор 
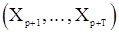и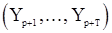 
связаны преобразованием
.....................................
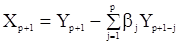
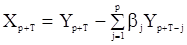
с единичным якобианом.
Следовательно,
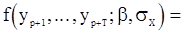
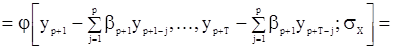
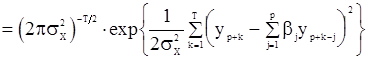(101)
Кроме того,
,
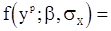
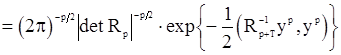Учитывая эту формулу и (101), запишем (99) в виде
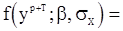
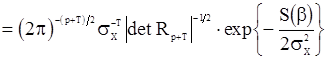, (102)
В предыдущей формуле
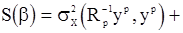
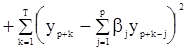(103)
Заметим, что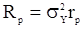 
, где 
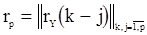- матрица, составленная из значений нормированной корреляционной функции, не зависящих от 
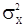, а величина 
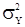, согласно формуле (15), пропорциональна 
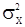. Следовательно 
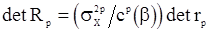и 
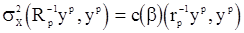, где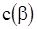 
- знаменатель правой части (15). Тогда логарифм функции правдоподобия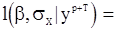 
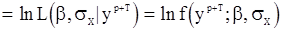будет иметь вид
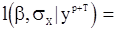
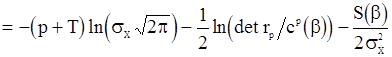. (104)
Наряду с параметрами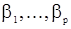 
будем считать неизвестной также дисперсию 
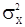входной последовательности. Тогда уравнения правдоподобия запишутся в виде
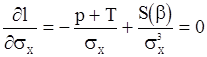, (105)
,
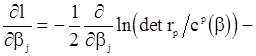
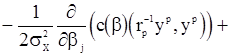
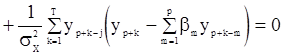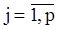. (106)
Выражая дисперсию «шума»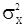 
из (105) и подставляя ее в систему (106), будем иметь систему относительно неизвестного вектора 
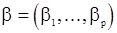. Однако при решении получающейся системы возникают трудности, поскольку в общем случае величины
, 
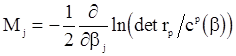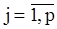
- сложные функции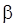 
. Продемонстрируем эти трудности на простейших случаях.
1. С.п.АР(1). В этом случае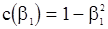 
, 
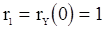и из (105) и (106) получаем кубическое уравнение относительно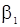 
,
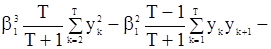
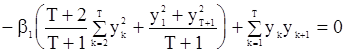корни которых в принципе могет быть точно найдены с использованием формул Г.Кардано. Однако если все три корня вещественны, то предстоит еще выяснить, какой из них доставляеи величине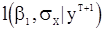 
наибольшее значение.
2. С.п.АР(2). Имеем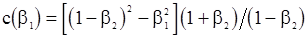 
,
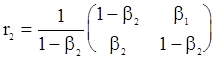
и система (106) получает вид
,
,
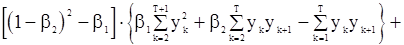
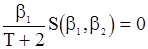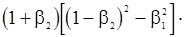
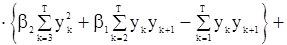
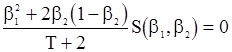где
.
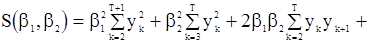
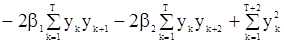В этом случае точное решение системы относительно неизвестных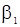 
и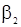 
уже не может быть найдено.
Итак, для получения оценки вектора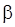 
в общем случае нужно либо искать приближенное решение системы (106), либо, отказавшись от ее решения, максимизировать вместо логарифма функции правдоподобия другую, но близкую к нему в каком-то смысле функцию. Ясно, что второй подход приведет к оценкам, которые не будут оценками м.п., но их все-таки естественно называть оценками квазимаксимального правдоподобия.
Оценки квазимаксимального правдоподобия. Примем во внимание, что в логарифме функции правдоподобия (104) слагаемое, содержащее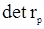 
, не зависит от T и мало по сравнению с остальными двумя слагаемыми, растущими с ростом T. Пренебрегая этими слагаемыми, получим функцию
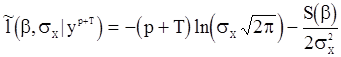. (107)
Крому того заметим, что величина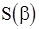 
, определенная неравенством (103), не только квадратичная форма от наблюдений 
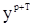, но (как показано в работе [3,с.304]) и от параметров 
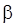. Если положить 
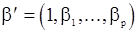, то для некоторой матрицы D размера (p+1)x(p+1) справедливо равенство
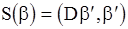, (108)
причем
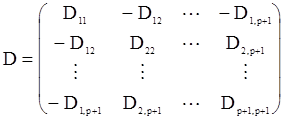(109)
а элементы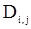 
определяются как суммы
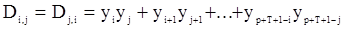(110)
содержащие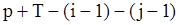 
слагаемых. Тогда оценки 
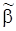параметров 
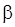, полученные путем максимизацмм (107), совпадают с оценками наименьших квадратов, полученными минимизацией 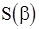. Дифференцируя (108) по 
, 
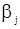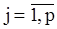и приравнивая к нулю соответствующие производные, получим систему
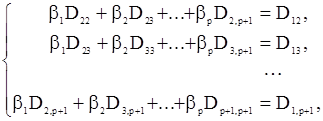(111)
которая в очевидных матричныз обозначениях имеет вид
,
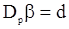откуда получаем оценку квазиоптимального правдоподобия
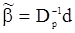(112)
Приближенные оценки м.п. параметров 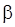можно получить изменяя сами уравнения правдоподобия (106). Сначала производную 
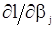запишем в виде
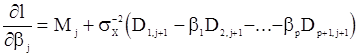, (113)
.
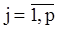Беря математические ожидания от обеих частей этих равенств и учитывая, что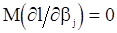 
, получаем
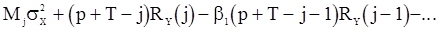
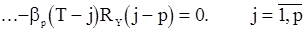. (114)
Теперь вспомним разностное уравнение (11) и, умножим его на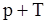 
, запишем в виде
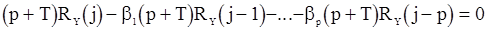
и вычтем из (114). Получим
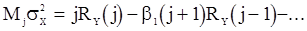
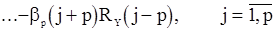. (115)
Используя в качестве оценок значений корреляционной функции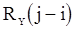 
величины 
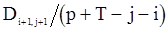, из (115) получим оценку для 
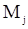, а подставляя ее в (113), получим
,
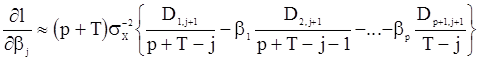что ведет к системе линейных уравнений согластно формуле (111), в которых вместо 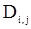стоят величины
.
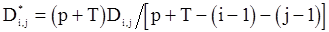В очевидных матричных обозначениях мы будем иметь систему
,
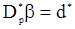из которых получаем приближенную оценку м.п.
.
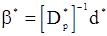Продемонстрируем различия рассмотренных оценок параметров 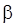на частных случаях 
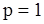и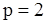 
.
1. С.п.АР(1). В этом случае оценка квазимаксимального правдоподобия находится по формуле (112), в которо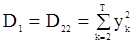й
и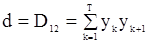 
.
Тогда
.
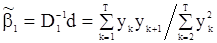Приближенная оценка м.п. определяется формулой (116), в которой
, 
.
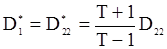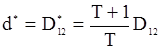Тогда
.
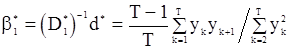2. С.п.АР(2). Для получения оценки квазимаксимального правдоподобия вектора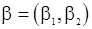 
нужно иметь вектор 
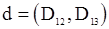и матрицу
,
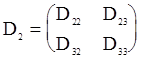причем выражения для величин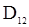 
и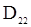 
указаны в предыдущем примере, а 
, 
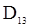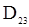и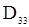 
имеют следующий вид:
, 
, 
.
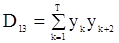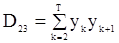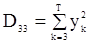Используя (112), находим
,
.
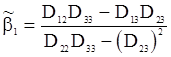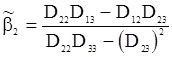Приближенная оценка м.п.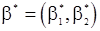 
вектора 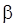может быть получена из предыдущих формул, в которых величины 
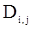нужно заменить величинами
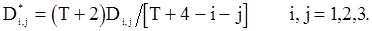
Рассмотренные примеры показывают, что для больших выборок различия между оценками, полученными путем разных приближений, малы. То же самое можно сказать об оценках параметров АР(p) и в общем случае.
М.м.п. для с.п. СС( q ) . Предположим, что на входе модели скользящего среднего (32) имеем гауссовский «шум»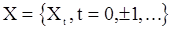 
с 
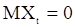и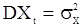 
. При этом выходной «сигнал» 
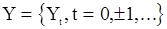тоже будет гауссовским и стационарным с 
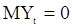и корреляционной функцией, определяемой формулой (33). Рассмотрим функцию правдоподобия для с.п.Y соответствующую наблюдениям 
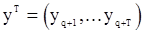. Гауссовский вектор 
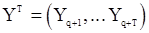будет иметь плотность распределения вида
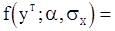
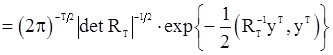, (117)
где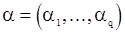 
- вектор параметров модели (32) 
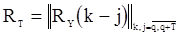- корреляционная матрица вектора 
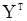с элементами, определяемыми по формуле (33). Хотя формула (33) проста, обращение матрицы 
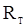при достаточно больших T сопряжено со значительными вычислительными трудностями. Поэтому рассмотрим удобный способ вычисления квадратичной формы 
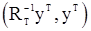. Для этого рассмотрим вектор 
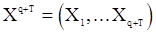, плотность распределения которого имеет вид
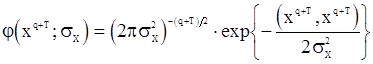(118)
и вектор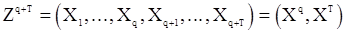 
, который связан с 
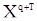линейным преобразованием в соответствии с (32):
.
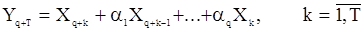При этом мы можем записать представление
,
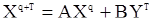где A - матрица размером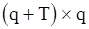 
, а B - матрица размером 
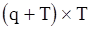. Элементы этих матриц представляют собой функции параметров 
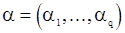. Замечая, что преобразование вектора 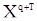в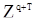 
имеет единичный якобиан, можем записать совместную плотность 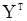и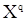 
,
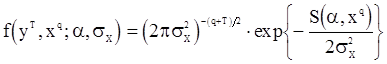где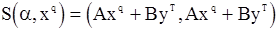 
.
Вектор предварительных значений «шума»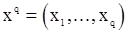 
на практике обычно не наблюдается, и мы найдем для него линейную относительно 
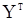оценку, минимизирующую 
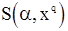. Пусть 
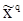некоторая оценка (функция наблюдения 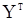) вектора 
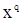. Запишем вектор
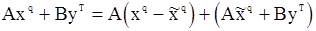
и подставим его в выражение для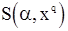 
. Получим равенство
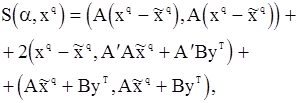
где штрих обозначает транспонирование матрицы. Если выбрать 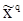так, что
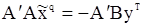(119)
то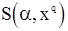 
будет иметь вид
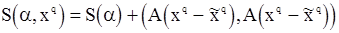(120)
где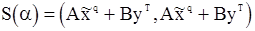 
- функция только наблюдений 
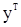, но не предварительных значений «шума».
Из (120) видно, что 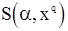достигает минимума при 
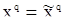, т.е 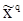- оценка наименьших квадратов. При этом совместную плотность 
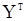и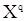 
можно представить в виде
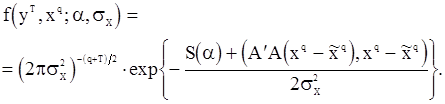
С другой стороны, ей можно придать вид
,
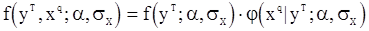где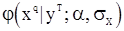 
- условная (гауссовская) плотность предварительных значений «шума» при фиксированных наблюдениях 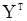. Следовательно
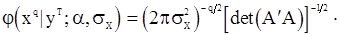
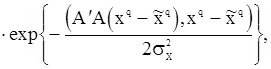(121)
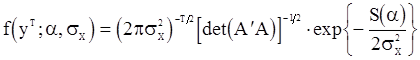(122)
Сделаем следующие выводы
1. Из (121) видно, что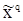 
является условным математическим ожиданием вектора 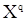при заданных при наблюдениях 
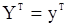и фиксированном 
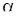. Используем обозначение
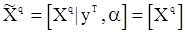
имеем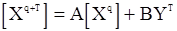 
и
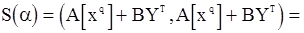
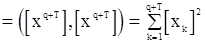. (123)
Хотя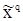 
можно получить непосредственно методом наименьших квадратов, на практике его легче вычислять, используя тот факт, что 
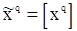, и получая 
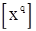по методике «прогнозирования» назад описанной в работе [3,разд.7.1.4 и 7.1.5]
Сравнивая (122) и (117), получаем
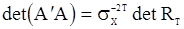
и
.
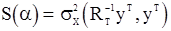Чтобы вычислить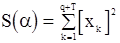 
, можно получить величины 
, 
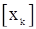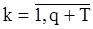, пользуясь оценками предварительных значений «шума»
,
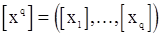полученных методом наименьших квадратов (или по методике «прогнозирования назад»), и, вычислив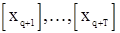 
- реккурентным путем по формулам, получающимся из (32), применяя к обеим частям равенства операции условного математического ожидания при фиксированных наблюдениях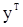 
, 
,
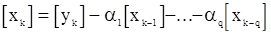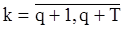где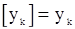 
.
Наконец, пользуясь (122) и (123), получаем точное выражение для безусловной функции правдоподобия
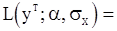
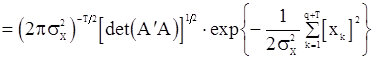. (124)
Таким образом, принципиально открыт путь к получению оценок м.п. Если наряду с 
неизвестно и 
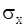, то уравнения правдоподобия будут иметь вид
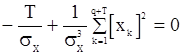(125)
и
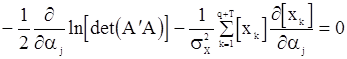(126)
где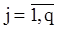 
.
Следует отметить, что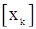 
- всегда нелинейные функции параметров 
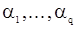. Если оценки параметра уже найдены, то подставив их в величины 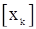, из (125) получаем оценку для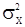 
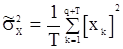. (127)
Сами же оценки параметров 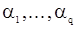могут быть найдены как решения системы (126), в которой вместо 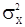следует подставить выражение, найденное из (125). Однако именно решение сисемы (126) представляет наибольшие трудности в силу ее нелинейности относительно . В отличие от с.п.АР(p) здесь не представляется возможным переход к линейной системе «квазимаксимального правдоподобия». Рассмотрим ситуацию с оцениванием в простейшем случае 
.
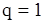Модель СС(1) определяется скалярным параметром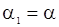 
, который и подлежит оценке. Матрица A в этом случае представляет собой вектор-столбец с элементами 
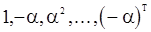. Тогда 
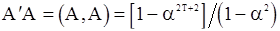и из (125) и (126) получаем уравнение
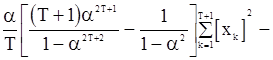
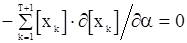(128)
Выразим величины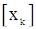 
, 
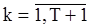через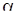 
и наблюдения 
, 
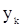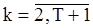. Оценку предварительного значения «шума» 
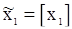можно найти из равенства (119). Легко убедиться, что в нашем примере матрица B имеет вид
,
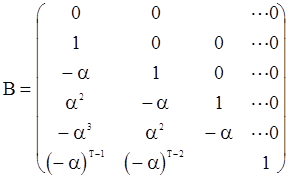а уравнение (119) можно записать в виде
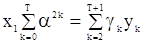
где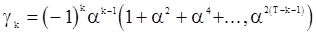 
, 
.
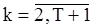Тогда
.
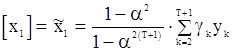Величины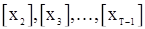 
можно теперь определить из реккурентных уравнений
, .
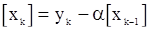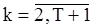Решение этих уравнений приводит к формулам
, 
.
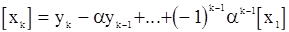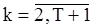После подстановки этих значений в (128) получим уравнение, содержащее кроме 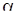лишь наблюдения 
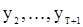. Однако точное решение полученного уравнения даже в этом простейшем частном случае мы найти не можем. Поэтому рассмотрим один из подходов к получению приближенных оценок м.п. вектора 
.
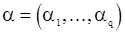Линеаризация модели. Рассмотрим в качестве «главной части» логарифма функции правдоподобия величину
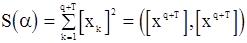
и будем ее минимизировать. Представляя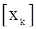 
по формуле Тейлора в окрестности точки, соответствующей предполагаемому значению параметра 
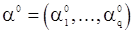получим приближенной равенство
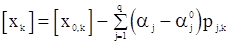, (129)
где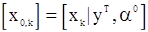 
, 
.
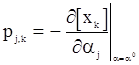В качестве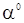 
можно использовать оценку вектора 
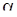, предварительно полученную по методу моментов с помощью линейно сходящегося итеративного процесса (см. разд. 3.3.). Если P - матрица с элементами 
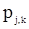размера 
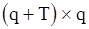, то 
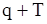уравнений (129) можно представить в виде
,
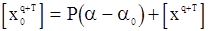где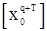 
и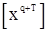 
- векторы-столбцы с 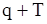элементами. Поправка 
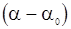, минимизирующая 
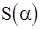, находится теперь линейным методом наименьших квадратов. Полагая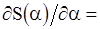 
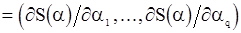, получаем
.
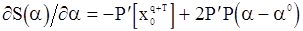Приравнивая этот вектор к нулевому находим
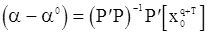. (130)
Поскольку 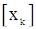не является линейной функцией параметров 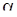, однократная поправка не обеспечит получение оценок наименьших квадратов. Поэтому полученные после первой поправки значения используются как новые предполагаемые значения, и процедура повторяется до получения сходящихся результатов. Сходимость оказывается более быстрой, если используются достаточно удачные начальные приближения. Если начальные приближения неудачны, то процесс вычисления параметров может оказаться расходящимся.
М.м.п. для смешанной модели АРСС( p,q ). Предположим теперь, что выходной сигнал 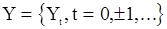порождается моделью (43), на входе которой имеем (как и в предыдущих случаях) гауссовский «шум» 
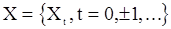с 
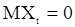и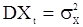 
. Считаем, что параметры авторегрессии 
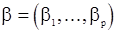обеспечивают стационарность выходного сигнала Y. Тогда Y - гауссовская стационарная с.п. с 
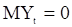и корреляционной функцией, определяемой уравнениями (46). Как в случае чистой с.п.СС(q), уравнения м.п. сложны и не поддаются непосредственному решению. Поэтому на практике можно использовать возможность представления с.п.АРСС(p,q) в виде чистой последовательности СС(¥) [2,с.264], которую в свою очередь заменяют конечной с.п.СС(Q):
,
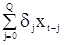где Q - невелико, а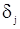 
- параметры, являющиеся функциями параметров 
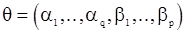исходной последовательности Y.
Для оценки параметра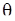 
в модели (131) теперь можно использовать, например, описанную выше «линеаризацию модели». Иногда для получения оценок, близких к оценкам м.п., можно следовать более прямым путем. Расмотрим пример.
Модель АРСС(2,1) описывается разностным уравнением
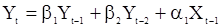(132)
в котором оценке подлежит параметр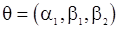 
. Полагая 
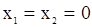из (132) получаем
,
,
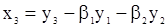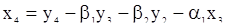и т.д. Оценка вектора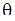 
может быть получена по наблюдениям 
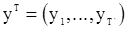путем минимизации величины
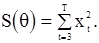
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Журбенко И.Г. Кожевникова И.А. Стохастическое моделирование процессов. М.:Изд-во МГУ, 1990 148с.
2. Андерсон Т. Стохастический анализ временных рядов. М.:Мир, 1976 757с.
3. Бокс Дж. Дженникс Г. Анализ временных рядов. Прогноз и управление. М.:Мир, 1974 Вып.1 406с.
4. Дианова Р.С. Моделирование случайных процессов и оценка их параметров. Учеб.пособие. Моск. Авиац. Ин-т. М., 1989 44с.
5. Харин Ю.С. Степанова М.Д. Практикум на ЭВМ по математической статистике. Минск: Изд-во Университетское, 304с.
6. Ивченко Г.И. Медведев Ю.И. Математическая статистика. М.: Высш.шк. 1984, 248с.
7. Бендат Дж. Присон А. Прикладной анализ случайных данных. М.:Мир 1989 541с.
Приложение 1
ПРОВЕРКА ГИПОТЕЗЫ СЛУЧАЙНОСТИ
Входную с.п.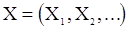 
часто предролагают «чисто случайной», т.е считают с.в. 
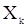независимыми и одинаково распределенными. Это предположение, как правило, оправдано и вытекает из самого характера задачи, но иногда оно нуждается в проверке. Математически задачу можно сформулировать следующим образом: проверить гипотезу 
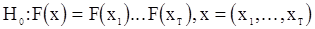, где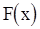 
- некоторая функция распределения. Такую гипотезу назавают гипотезой случайности. Критерий согласия для проверки этой гипотезы можно построить [6] исходя из следующих соображений (далее предполагается, что вектор 
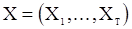имеет непрерывное распределение).
Если гипотеза случайности действительно имеет место, то компоненты вектора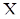 
«равноправны» и поэтому данные наблюдения не должны быть ни в каком смысле упорядоченны. Другими словами, ситуацию, соответствующую гипотезе 
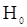, можно охарактеризовать как «полный хаос» или «полный беспорядок». При отклонениях от 
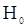исходные данные имеют тот или иной порядок. Следовательно, критерий проверки 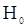можно построить на основании статистик, измеряющих степень «беспорядка» исходных данных. Одной из таких статистик является число инверсий ввыборке. Эта статистика определяется следующим образом. Построим вариационный ряд 
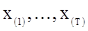выборки 
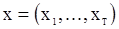. Говорят, что компоненты 
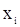и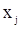 
образуют инверсию, если 
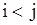, но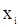 
стоит правее 
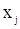в вариационном ряду т.е. наблюдению с меньшим номером соответствуют большее значение.
Если для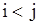 
положить
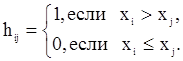
то число инверсий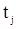 
, образованных компонентный 
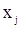(в вариационном ряду левее 
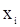стоит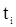 
элементов выборки с большими номерами), определится равенством
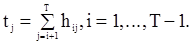
Тогда общее число инверсий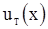 
для выборки 
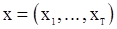будет задано равенство
.
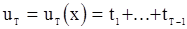Статистика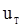 
является естетственной мерой «беспорядка» среди наблюдений и ее можно использовать для проверки гипотезы 
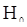. Краиние случаи, когда вариационный ряд имеет вид 
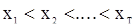или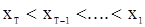 
естетственно рассматривать как свидетельства «полного отсутствия беспорядка», т.е. противоречашее гипотезе 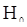. В первом случае статистика 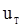принимает минимальное значение, равное 0, а во втором случае она максимальна и равна 
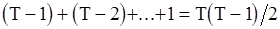. Таким образом, слишком малые и слишком большие значения 
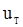(близкие к 
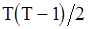) естетственно рассматривать как критические для гипотезы 
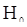. Чтобы определить числовые характеристики этого критерия, найдем распределение статистики 
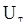при гипотезе .
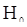Из соображений симметрии ясно, что при гипотезе 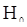любое из 
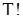относительных расположений элементов выборки в соответствующем вариационном ряду имеет одинаковую вероятность 
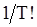. Введенная с.в. 
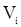определяется расположением с.в. 
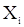по отношению к 
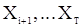в вариационном ряду и не зависит от относительного расположения последних между собой, т.е 
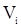при любом 
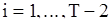не зависит от 
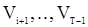взаимно независимы. При этом величина 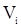может с одной и той же вероятностью 
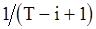принимать значения 
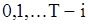, поэтому ее производящая функция имеет вид
,
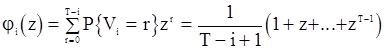а производящая функция статистики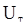 
представлена следующим образом:
.
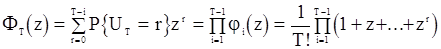Отсюда имеем
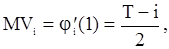
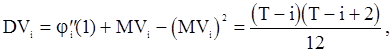
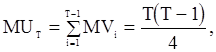
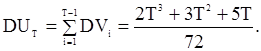
Итак, среднее значение статистики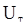 
при нулевой гипотезе совпадает с серединой промежутка 
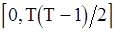, и в критическую область 
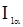следует включать все целые точки этого промежетка, достаточно удаленные от середины. При заданном уровне значимости 
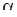в качестве области принятия нулевой гипотезы можно взять промежуток
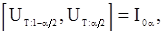
где величины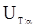 
определяются из условия
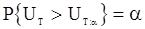
Разлагая функцию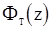 
в ряд по степеням 
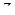и вычисляя коэффициент при 
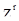, можно вычислить вероятности 
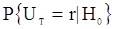при заданном 
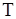и любом 
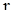и использовать их для нахождения границы 
.
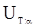Приведем небольшую таблицу из работы [7], содержащую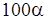 
- процентные точки функции распределения с.в. .
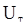Таблица
Процентные точки рапределения числа инверсий
| T |
| |||||
| 0,99 | 0,975 | ,095 | 0,05 | 0,025 | 0,01 | |
| 10 | 9 | 11 | 13 | 31 | 33 | 35 |
| 12 | 16 | 18 | 21 | 44 | 47 | 49 |
| 14 | 24 | 27 | 30 | 60 | 63 | 66 |
| 16 | 34 | 38 | 41 | 78 | 81 | 85 |
| 18 | 45 | 50 | 54 | 98 | 102 | 107 |
| 20 | 59 | 64 | 69 | 120 | 125 | 130 |
| 30 | 152 | 162 | 171 | 263 | 272 | 282 |
| 40 | 290 | 305 | 319 | 460 | 474 | 489 |
| 50 | 473 | 495 | 514 | 710 | 729 | 751 |
| 60 | 702 | 731 | 756 | 1013 | 1038 | 1067 |
| 70 | 977 | 1014 | 1045 | 1369 | 1400 | 1437 |
| 80 | 1299 | 1344 | 1382 | 1777 | 1815 | 1860 |
| 90 | 1668 | 1721 | 1766 | 2238 | 2283 | 2336 |
| 100 | 2083 | 2145 | 2198 | 2751 | 2804 | 2866 |
Примечание.Значения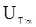 
такие, что 
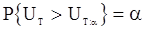, где 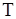- общее число наблюдений.
Пусть имеется следующая последовательность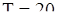 
наблюдений некоторой с.в.
| 1. 5,5 | 6. 5,7 | 11. 6,8 | 16. 5,4 | ||
| 2. 5,1 | 7. 5,0 | 12. 6,6 | 17. 6,8 | ||
| 3. 5,7 | 8. 6,5 | 13. 4,9 | 18. 5,8 | ||
| 4. 5,2 | 9. 5,4 | 14. 5,4 | 19. 6,9 | ||
| 5. 4,8 | 10. 5,8 | 15. 5,9 | 20. 5,5 |
Гипотеза заключается в том, что эти наблюдения представляют собой независимые исходы (измерения) с.в.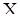 
, и ее надо проверить при заданном уровне значимости 
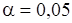. Подсчитаем число инверсий в последовательности
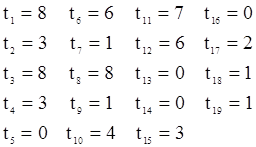
Общее число инверсий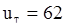 
. Область принятия имеет вид
.
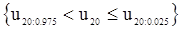Из таблицы при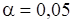 
находим 
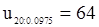и 
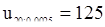. Следовательно, гипотеза должна быть отвергнута с уровнем значимости 5%, т.к. 
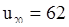не попадает в промежуток между 64 и 125ю
Для большой «длины» релизации 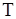применяют простой асимптотический вариант этого критерия. Используя производящую функцию 
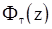, можно показать, чтохарактеристическая функция нормированной статистики 
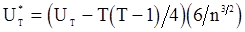сходится при 
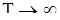и любом конечном 
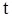к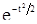 
- характеристической функции нориального распределения. Это означает, что распределение величины 
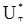слабо сходится к нормальному закону 
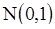при .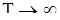
Последний результат дает возможность сформулировать следующее правило проверки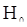 
, когда значение 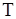велико: для заданного уровня значимости 
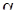определяют число 
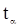из условия 
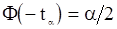; по фактически наблюдающимся данным 
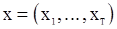вычисляют значение 
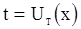числа инверсий в выборке. Если 
, то гипотезу 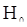отвергают ка противоречащую исходным данным. В противном случае признают, что гипотеза независимости и одинаковой распределенности наблюдений согласуется с опытными данными.
Вероятность ошибочно отвергнуть при этом истинную гипотезу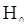 
.
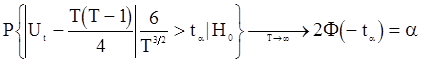Это правило можно использовать уже при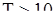 
.
Приложение 2
ПРОВЕРКА СТАЦИОНАРНОСТИ
Изложенные в основном тексте настоящего пособия методы статистической обработки временных рядов подразумевают стационарность последних. Стацинарность процесса играет важную роль потому, что методы анализа нестационарных процессов существенно более громозки, чем в стационарном случае. Часто стационарность вытекает из физической природы процесса, когда порождающие его факторы не зависят от времени. Однако далеко не всегда имеется априорная информация, позволяющая считать исследуемый процесс стационарным. Даже если временной ряд получается путем статического моделирования на компьютере, то не всегда удается обеспечить его стационарность с самого начала процесса моделирования. В частности, при моделировании с.п.АРСС с негауссовским шумом начальный «отрезок» выходного процесса может быть далек от стационарности, и возникает необходимость выбора для статистической обработки участка реализации, соответствующего установившемуся (стационарному) режиму. В Любом случае когда нужно убедится в стационарности наблюдений, поступивших для обработки, приходится использовать один из статистических критериев для проверки гипотезы стационарности.
Стационарность в узком смысле означает, как известно, независимость конечномерных распределений от сдвига по временной оси. Это значит, что функция распределния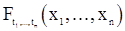 
процесса 
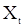удовлетворяет условию
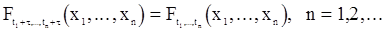
для любых значений аргументов и таких любых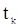 
и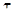 
, что и 
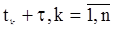принадлежат допустимому множеству временного параметра 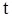. Очевидно, что в этом случае для любой измеримрй функции 
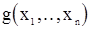случайные величины
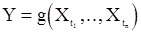и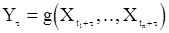 
одинаково распределены, а моментные функции, если они существуют, не зависят от сдвига по времени.
Если исследователя интересует не сами конечномерные распределения процесса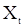 
, а лишь его моментные функции, то целесообразно пользоваться определениями стационарности, основанными на свойствах моментных функций.
Стационарным в широком смысле k-го порядка называют процесс 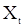, у которого моментные функции до k-го порядка включительно существуют и не зависят от сдвига по времени. При этом чаще всего речь идет о процессах, стационарных в широком смысле 2-го порядка, которые называются просто стационарными в широком смысле. Для них 
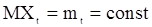и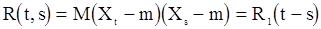 
.
Отметим, что если процесс стационарен в узком смысле и обладает моментными функциями до k-го порядка, то он является стационарным и в широком смысле k-го порядка. В случае гауссовских процессов стационарность в широком смысле 2-го порядка будет означать и стационарность в узком смысле, поскольку все конечномерные распределения гауссовского процесса вполне определяются двумя первыми моментными функциями: средним значением и корреляционной функцией.
Перейдем к рассмотрению задачи проверки гипотезы стационарности по существу. Мы используем знакомый из предшествующего раздела критерий инверсий. К сожалению, при построении такого критерия не удается обойтись только одной реализацией. Итак, предположим, что исследуется случайный процесс с дискретным временем, т.е. случайная последовательность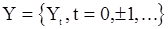 
, относительно которой нужно проверить гипотезу 
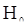: «с.п. 
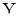стационарна в узком смысле». Рассмотрим 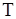независимых наблюдений последовательности 
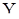, причем k-e наблюдение имеет длину nk, где n- некоторое положительное число. Тогда первое наблюдение представляет собой реализацию с.п. 
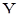длины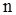 
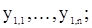
k-ое наблюдение - реализацию длины kn
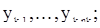
а последнее наблюдение (с номером 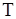) - это реализация длины nT
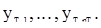
С помощью некоторой измеримой функции n переменных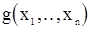 
построим используя n последниу значения каждой из 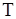полученных реализаций, величины:
.
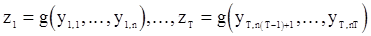Если в них значения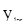 
заменить случайными случайными величинами 
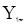из последовательности 
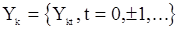, являющейся k-ой (по порядку) «копией» исследуемой с.п. 
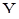, то получим случайные величины
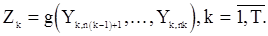
Они будут независимы в совокупности, т.к. порождаются независимыми «копиями» с.п.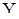 
. В случае же справедливости гипотезы 
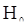, т.е. в случае стационарности в узком смысле с.п. 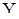, они будут одинаково распределенными. Таким образом, гипотеза 
будет подтверждатся или отвергатся одновременно с принятием или отклонением гипотезы случайности для с.в.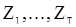 
при любой генерирующей их функции 
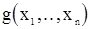. Для проверки же гипотезы случайности можно использовать изложенный в прил.1 критерий инверсий.
При описанном выше подходе к проверке гипотезы стационарности функцию 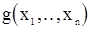цедесообразно выбирать так, чтобы величины 
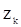представляли собой выборочные моменты. Если существует, в частности, моментная функция r-го порядка и гипотеза 
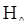верна, то выбирая функцию
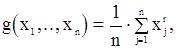
в качестве 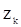будет иметь оценку начального момента r-го порядка
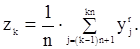
При достаточно слабых ограничениях эта оценка состоятельна:
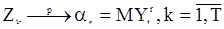при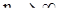 
.
Поэтому при истинности гипотезы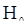 
величины 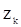не должны существенно зависеть от времени (от индекса k). Если же они сильно колеблются в зависимости от k, то это свидетельствует о том, что наблюдения не согласуются гипотезой стационарности и можно не пренебрегать к использованию критерия инверсий. В случае отсутствия явный колебаний в совокупности 
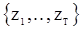придется пользоваться критерием инверсий.
На практике для проверки гипотезы 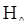можно рекомендовать построение критерия инверсий на основе совокупности оценок момента второго порядка
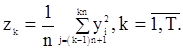
Дата: 2019-04-23, просмотров: 201.
