При изучении систем, осуществляющих преобразования входных случайных сигналов, приходится решать ряд статистических задач. Прежде всего это задачи определения вероятностных характеристик входных и выходных сигналов, а также задачи проверки гипотез об этих сигналах. Кроме того, часто неизвестной или частично известной является сама преобразующая система. В простых случаях она бывает известной с точностью до конечной совокупности определяющих ее параметров. Задачи статистических выводов в этом случае связаны с этими параметрами и включаются в так называемые методы идентификации, призванные по экспериментальным данным определить тип преобразующей системы. Все упомянутые задачи решаются на основе обработки экспериментального материала и относятся к сравнительно новой ветви математической статистики, называемой статистикой случайных процессов. Применяемые в статистике случайных процессов (и, в частности, случайных последовательностей) методы принципиально не отличаются от обычных методов обработки, используемых в математической статистике (МС), однако имеются некоторые особенности, осложняющие решение задач. Как известно, все оценки и критерии в МС строятся на основе выборки
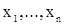 (61)
(61)
где n - объем выборки, а ее элементы 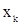 являются значениями исследуемой с.в. X при независимых измерениях. Поэтому выборку (16) в МС рассматривают как реализацию случайной последовательности «длины» n независимых с.в.
являются значениями исследуемой с.в. X при независимых измерениях. Поэтому выборку (16) в МС рассматривают как реализацию случайной последовательности «длины» n независимых с.в. 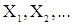 с общим распределением, совпадающим с распределением исследуемой с.в.X. В статистике случайных процессов по ряду причин основой не могут служить независимые реализации процесса (или последовательности) Y, и поэтому теряет смысл понятие объема выборки n, входящего явно в известные в МС формулы для критериев и оценок. Аналогичную объему выборки роль в статистике случайных процессов играет «длина» времени, в течении которого наблюдается реализация процесса. Если Y- случайная последовательность:
с общим распределением, совпадающим с распределением исследуемой с.в.X. В статистике случайных процессов по ряду причин основой не могут служить независимые реализации процесса (или последовательности) Y, и поэтому теряет смысл понятие объема выборки n, входящего явно в известные в МС формулы для критериев и оценок. Аналогичную объему выборки роль в статистике случайных процессов играет «длина» времени, в течении которого наблюдается реализация процесса. Если Y- случайная последовательность: 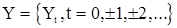 , то реализация, наблюдаемая в моменты t=1,...T, будет представлять собой совокупность значений
, то реализация, наблюдаемая в моменты t=1,...T, будет представлять собой совокупность значений
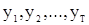 , (62)
, (62)
которая и служит основой для статистических выводов.
Мы здесь имеем возможность рассмотреть только некоторые задачи статистической обработки реализаций с.п. в предположении их стационарности. Предположим известными основные факты МС независимых наблюдений.
Некоторые дополнительные сведения содержаться в прил.1 и 2 настоящего пособия. При исследовании входной случайной последовательности 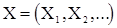 одной из важнейших является задача проверки гипотезы о том, что случайные величины
одной из важнейших является задача проверки гипотезы о том, что случайные величины 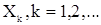 независимы и одинаково распределены. Один из критериев проверки такой гипотезы изложен в прил.1. Прил.2. содержит описание одного из возможных критериев проверки гипотезы стационарности.
независимы и одинаково распределены. Один из критериев проверки такой гипотезы изложен в прил.1. Прил.2. содержит описание одного из возможных критериев проверки гипотезы стационарности.
Следующий раздел данного учебного пособия содержит традиционный материал по оцениванию среднего значения и корреляционной функции стационарных последовательностей и не связан прямо с последовательностями авторегрессии и скользящего среднего. Остальной материал раздела посвящен решению статистических задач АР и СС. Следует отметить, что основная статистическая задача оценивания параметров АР и СС может иметь различные интерпретации. Ее можно, в частности, трактовать как оценивание спектра, а также и как задачу идентификации системы, структура которой определена с точностью до неизвестных параметров.
Оценка среднего значения
И корреляционной функции
Пусть 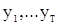 - T последовательных наблюдений с.п.
- T последовательных наблюдений с.п. 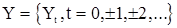 , стационарной в широком смысле со средним значением
, стационарной в широком смысле со средним значением 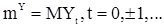 , и корреляционной функцией
, и корреляционной функцией 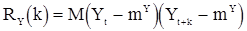 ,
, 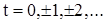 ,
, 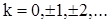 ,
, 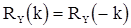 .
.
Рассмотрим сначала оценивание среднего значения 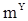 . Будем искать оценку величины
. Будем искать оценку величины 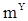 в классе линейных оценок, т.е. среди линейных комбинаций наблюдений
в классе линейных оценок, т.е. среди линейных комбинаций наблюдений
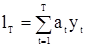 . (63)
. (63)
Среднее значение и дисперсия произвольной линейной комбинации (63) соответственно равны
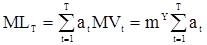 (64)
(64)
и
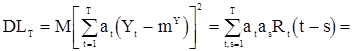
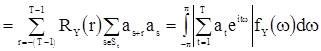 , (65)
, (65)
где 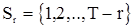 при
при 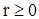 и
и 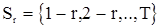 при
при 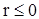 . Для того, чтобы с.в.
. Для того, чтобы с.в. 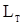 была несмещенной оценкой среднего значения
была несмещенной оценкой среднего значения 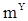 , должно выполнятся равенство
, должно выполнятся равенство
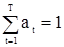 (66)
(66)
По обычным правилам отыскания условного экстремума находим вектор 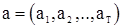 , обеспечивающий минимальную дисперсию несмещенной оценке
, обеспечивающий минимальную дисперсию несмещенной оценке
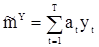 ,
, 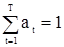 . (67)
. (67)
Несложные выкладки показывают, что несмещенная линейная оценка с минимальной дисперсией задается формулой (67) при векторе коэффициентов
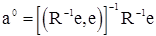 , (68)
, (68)
где 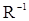 - матрица, обратная к корреляционной матрице наблюдений
- матрица, обратная к корреляционной матрице наблюдений 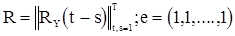 - единичный вектор, а (.,.) - скалярное произведение n-мерном евклидовом пространстве. Таким образом, оптимальная линейная несмещенная оценка будет иметь вид
- единичный вектор, а (.,.) - скалярное произведение n-мерном евклидовом пространстве. Таким образом, оптимальная линейная несмещенная оценка будет иметь вид
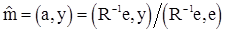 . (69)
. (69)
где 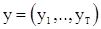 - вектор наблюдений, а дисперсия этой оценки определяется равенством
- вектор наблюдений, а дисперсия этой оценки определяется равенством
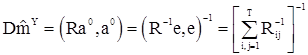 (70)
(70)
где 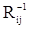 - элементы матрицы
- элементы матрицы 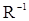 .
.
На практике часто в качестве несмещенной оценки среднего значения стационарной с.п. используется среднее арифметическое наблюдений
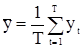 (71)
(71)
Используя формулу (65) получим дисперсию этой оценки
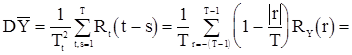
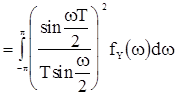 . (72)
. (72)
Асимптотическое (при 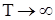 ) поведение дисперсии среднеарифметической оценки величины
) поведение дисперсии среднеарифметической оценки величины 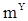 дается следующей теоремой.
дается следующей теоремой.
Теорема 3. Если выполняется условие
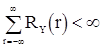 , (73)
, (73)
то оценка (71) состоятельна и
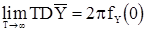 . (74)
. (74)
Доказательство состоятельности оценки 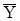 следует из того, что при условии (73)
следует из того, что при условии (73) 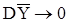 при
при 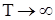 . Основанием соотношения (74) является известный из анализа факт.
. Основанием соотношения (74) является известный из анализа факт.
Лемма. Если ряд 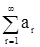 сходится, то
сходится, то
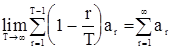 . (75)
. (75)
Соотношение (75) следует из (74), если учесть разложение вида (5) спектральной плотности в ряд Фурье, полагая в нем 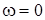 .
.
Теперь рассмотрим оценивание корреляционной функции. Если 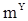 известно, то обычно используется оценка
известно, то обычно используется оценка
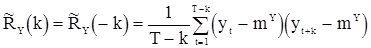 , (76)
, (76)
где 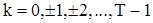 .
.
Если 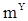 неизвестно, то по аналогии можно построить следующую оценку:
неизвестно, то по аналогии можно построить следующую оценку:
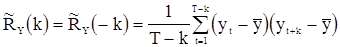 , (77)
, (77)
где 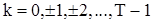 .
.
Возможны еще и другие оценки, в частности
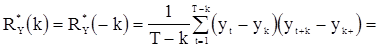
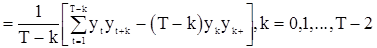 ,
,
где
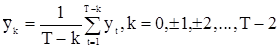 ,
,
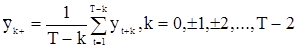 .
.
Рассмотрим моменты первого и второго порядков оценок величины 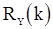 . Непосредственные вычисления дают следующие результаты. В случае известного среднего
. Непосредственные вычисления дают следующие результаты. В случае известного среднего 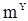
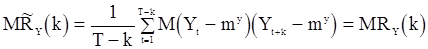 , (78)
, (78)
т.е. оценка 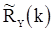 является несмещенной. В случае неизвестного
является несмещенной. В случае неизвестного 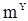 для математического ожидания оценки
для математического ожидания оценки 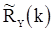 после несложных, но утомительных вычислений получаем соотношения:
после несложных, но утомительных вычислений получаем соотношения:
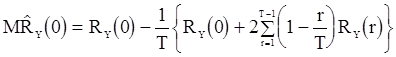 ; (79)
; (79)
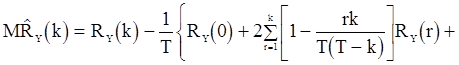
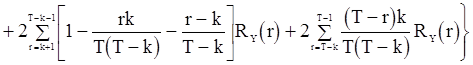 (80)
(80)
если 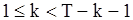 ;
;
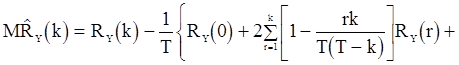
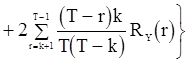 , (81)
, (81)
если 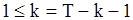 ;
;
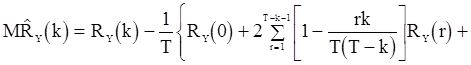
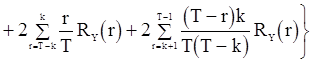 , (82)
, (82)
если 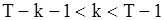 ;
;
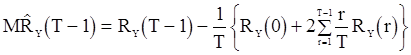 . (83)
. (83)
Формулы (79)-(83) показывают, что оценка 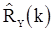 является смещенной, порядок смещения равен
является смещенной, порядок смещения равен 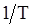 .
.
Математическое ожидание оценки 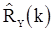 можно также выразить с помощью спектральной плотности
можно также выразить с помощью спектральной плотности
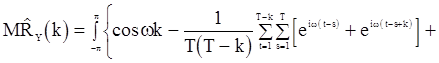
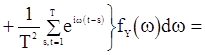
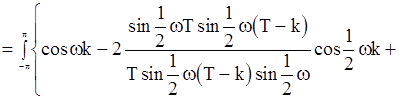
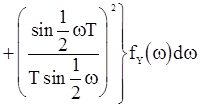 . (84)
. (84)
Аналогичные выражения можно получить и для математического ожидания оценки 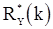 .
.
Ждя дисперсии несмещенной оценки 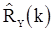 можно получить следующее выражение:
можно получить следующее выражение:
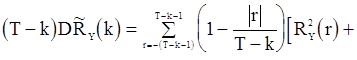
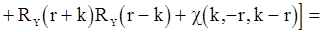
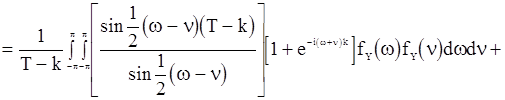
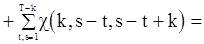
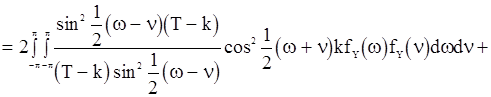
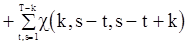
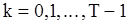 , (85)
, (85)
где 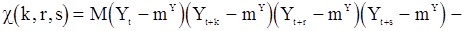
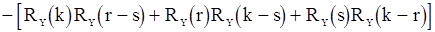 - семиинвариант четвертого порядка.
- семиинвариант четвертого порядка.
Если последовательность 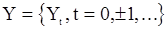 гауссовская, то семиинварианты четвертого порядка в выражениях (85) обращаются в нуль.
гауссовская, то семиинварианты четвертого порядка в выражениях (85) обращаются в нуль.
Более трудоемко вычисление выражений для дисперсий смещенных оценок 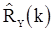 и
и 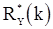 ; сами выражения дисперсий более громоздки и мы их не приводим.
; сами выражения дисперсий более громоздки и мы их не приводим.
Отметим некоторые ассимптотические свойства оценок корреляционоой функции. При известном среднем 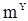 оценка
оценка 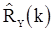 , как уже отмечалось выше, является несмещенной. При неизвестном среднем оценки
, как уже отмечалось выше, является несмещенной. При неизвестном среднем оценки 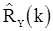 и
и 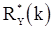 , как показывают, в частности, формулы (79)-(83), являются смещенными, причем смещение содержит множитель
, как показывают, в частности, формулы (79)-(83), являются смещенными, причем смещение содержит множитель 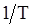 . Более точно поведение оценок
. Более точно поведение оценок 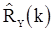 и
и 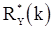 при
при 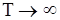 выражается следующей теоремой.
выражается следующей теоремой.
Теорема 4. Если 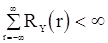 , то оценки
, то оценки 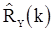 и
и 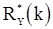 являются ассимптотическими несмещенными и
являются ассимптотическими несмещенными и
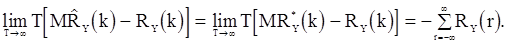 Если
Если 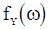 непрерывна при
непрерывна при 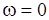 , то
, то
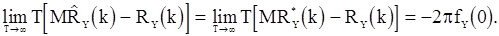
Вернемся к дисперсиям оценок корреляционной функции. Если для с.п. 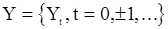 ,
, 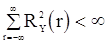 и
и 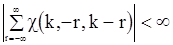 , то предельная дисперсия величины
, то предельная дисперсия величины 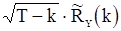 будет определятся соотношением
будет определятся соотношением
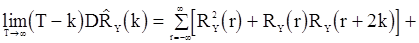
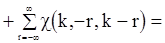
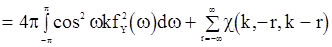 . (86)
. (86)
Соотношение (86) вместе с асимптотической несмещенностью означают состоятельность оценки 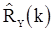 .
.
Если 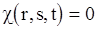 (что имеет место для гауссовских с.п.) и
(что имеет место для гауссовских с.п.) и 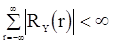 , то предельные дисперсии величин
, то предельные дисперсии величин 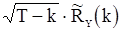 стремятся к
стремятся к 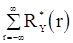 , когда
, когда 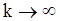 .
.
Можно установить, что если моменты с.п. 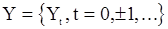 до четвертого порядка включительно соответствуют стационарности, и
до четвертого порядка включительно соответствуют стационарности, и
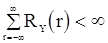 и
и 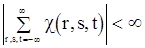 ,
,
то разность между 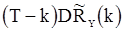 и
и 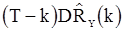 , а также между
, а также между 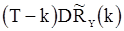 и
и 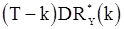 имеет порядок
имеет порядок 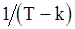 . Это означает, во-первых, что оценки
. Это означает, во-первых, что оценки 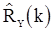 и
и 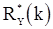 состоятельны, а, во-вторых, что для «больших выборок» величину
состоятельны, а, во-вторых, что для «больших выборок» величину 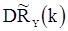 можно использовать как апроксимацию для
можно использовать как апроксимацию для 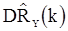 и
и 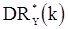 .
.
Дата: 2019-04-23, просмотров: 299.