Так называемая модель авторегрессии описывается стохастическим разностным уравнением вида

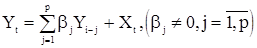,                   (7)
где t пробегает целые значения, а 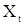- последовательность вещественнозначных некоррелированных и одинаково распределенных  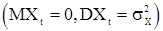случайных величин (с.в.). Последовательность  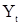называется с.п. авторегрессии порядка p, сокращенно АР(p). Большое практическое значение имеют последовательности авторегрессии первого (p=1) и (p=2) порядков

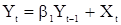  ,                                              (8)

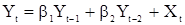.                                  (9)

Характеристическим уравнением для стохастического разностного уравнения (7) называют [2] алгебраическое уравнение

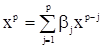.                                                (10)

Оно имеет p корней, которые мы обозначим 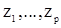. Корни характеристического уравнения (10) определяют важные свойства процесса 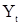, удовлетворяющего уравнению (7). Эти свойства можно сформулировать следующими теоремами.

Теорема 1. Если все корни характеристического уравнения (10) по абсолютной величине меньше 1, то 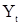 представим бесконечной линейной комбинацией с.в. 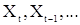, и, следовательно,  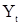не коррелирует со с.в. 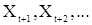. При этом последовательность  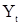будет стационарной (в широком смысле).

Замечание. Для стационарности с.п. 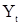, определяемой уравнением (7), от последовательности с.в.  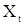в теореме 1 достаточно требовать лишь стационарности в широком смысле.

Теорема 2. Если стационарная с.п. 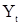 удовлетворяет уравнению (7), характеристическое уравнение (10) которого имеет хотя бы один корень, равный единице, то с вероятностью 1 все значения этой последовательности совпадают.

Доказательства этих теорем можно найти в работах [2,3].

В дальнейшем мы будем ограничиваться рассмотрением случая, когда все корни характеристического уравнения (10) по абсолютной величине меньше единицы. Получим важное рекуррентное соотношение, связывающее параметры 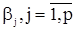 авторегрессии со значениями корреляционной функции выходной с.п.АР(p). Для этого умножим (7) на 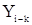и перейдем к математическому ожиданию. Учитывая при этом, что  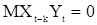при k>0, получаем

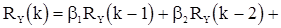
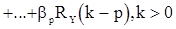                                   (11)
Уравнение (11) - разностное уравнение относительно R(k). Общее решение этого уравнения задается в виде

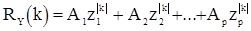,                   (12)
если корни 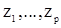 характеристического уравнения (10) различны. Граничными условиями будут p-1 соотношения

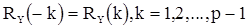                    (13)

и соотношение

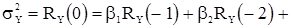
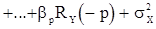                                       (14)
которое получается умножением (7) на 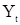 и переходом к математическому ожиданию в обеих частях полученного неравенства. Для определения коэффициентов  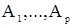сначала можно решить относительно  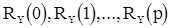систему из p уравнений вида (11) при k=1,2,...,p и уравнения (14), а затем относительно  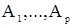решить систему уравнений вида (12) при k=0,1,...,p-1, подставляя вместо  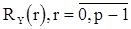предварительно найденные значения.

Вводя нормированную корреляционную функцию 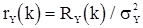 из (14), учитывая равенства (13), получаем выражение для дисперсии с.п.АР(p)

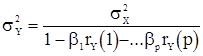                             (15)

Поделим все члены уравнения (11) на 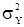 и подставив в него значения k=1,2,...,p, получим систему линейных уравнений для 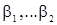со свободными членами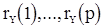

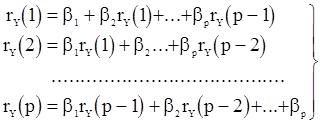
Эти уравнения обычно называются уравнениями Юла-Уокера и могут использоваться для получения оценок параметров .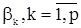

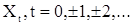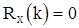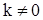Перейдем к рассмотрению спектра с.п.АР(p). Заметим, что входная с.п. имеет корреляционную функцию  при и 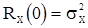. Этой корреляционной функции соответствует согласно (5) постоянная на  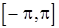спектральная плотность

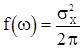.                                                    (16)
В силу теоремы Хинчина для последовательности 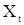 будет справедливо представление (6) с некоторым процессом с ортогональными приращениями 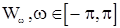. Выходная с.п.АР(p)  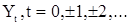будет иметь корреляционную функцию  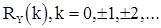удовлетворяющая рекуррентному соотношению (11), и сам процесс будет иметь также в силу теоремы Хинчина интегральное представление

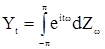                                                 (17)
с процессом, с ортогональными приращениями 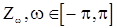, со структурной функцией 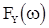, являющейся одновременно спектральной функцией последовательности 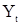. Подставляя в (7) вместо  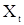его выражение из (6), а вместо 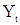- выражение из (17), получаем

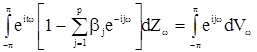                  (18)
Обе части этого неравенства - стохастические интегралы при любом целом t. Умножая (18) на такое же равенство при t-k(k-целое) и беря затем математическое ожидание от обеих частей полученного равенства, находим (с учетом свойств стохастических интегралов)

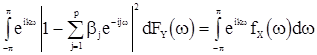.     (19)

Из (12) видно, что для стационарной с.п.АР(p) 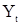 условие (2) выполняется и, следовательно, существует спектральная плотность 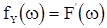. Тогда из равенства (19) получаем

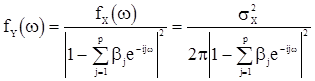.      (20)

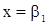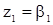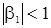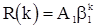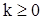Приведем основные характеристики с.п.АР(p) первого и второго порядков. При p=1 мы имеем дело со с.п.АР(1), определяемой уравнением (8). Ему соответствует характеристическое уравнение  с очевидным корнем . Это означает, что для стационарной с.п.АР(1) должно выполнятся условие . При этом из формулы (12) следует, что  для , где 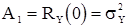. Согласно (15) для дисперсии  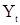получаем формулу

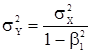,                                                   (21)
а для корреляционной функции

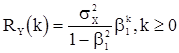.                                 (22)

Спектральная плотность с.п.АР(1) согласно (20) имеет вид

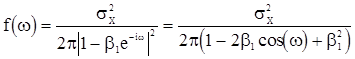. (23)

Теперь рассмотрим с.п.АР(2), определяемую уравнением (3). Характеристическое уравнение будет иметь вид

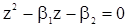                                            (24)
и с.п.АР(2) будет стационарной, если корни уравнения (24) лежат внутри единичного круга 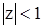, т.е.

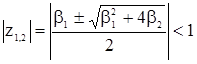.                             (25)
В случае действительных различных корней 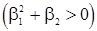 имеем неравенства  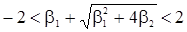и 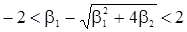. Это означает, что

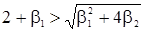 и 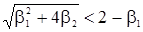,       (26)
откуда получаем

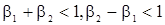.                                    (27)
Итак, область параметров 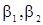, обеспечивающих различные действительные корни  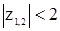уравнения (24), задается неравенством (27) и неравенством 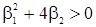. Найдем область параметров 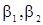, дающих комплексные (сопряженные) корни 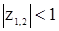. При этом дискриминант  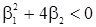и, следовательно, 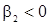. Условие (25) тогда можно представить в виде

.                                                    
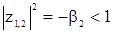Следовательно, интересующая нас область параметров 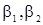, определяется неравенствам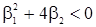и  и 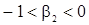. Результатам проведенного анализа дадим геометрическую иллюстрацию (рис.2) на плоскости .

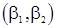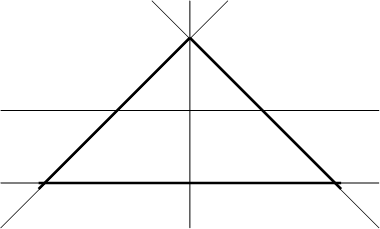Корреляционная функция с.п.АР(2) в соответствии с формулой (12) будет иметь вид

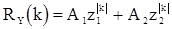
Записывая уравнения (14) и (11) для p=2 при k=1,2, получаем систему относительно

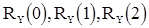
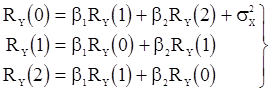
Решая ее, находим

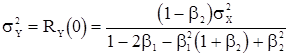            (28)

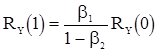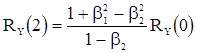, . (29)
Полагая, k=0 и k=1, получим систему

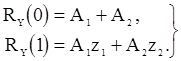
из которой находим

,

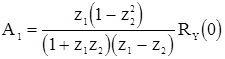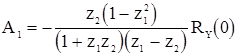.                     (30)
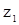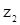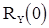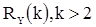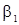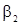Подставляем в эти формулы значения корней  и  квадратного уравнения (24) и  из (28), получим по формуле (12) значения корреляционной функции , выраженные через параметры  и . Для 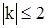 значения корреляционной функции определяются формулами (28) и (29).

В соответствии с формулой (20) получаем спектральную плотность с.п.АР(2)

,

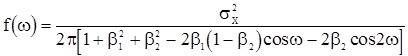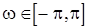.                                                   (31)