СТАТИСТИЧЕСКИЙ АНАЛИЗ
ВРЕМЕННЫХ РЯДОВ
АВТОРЕГРЕССИИ
И СКОЛЬЗЯЩЕГО СРЕДНЕГО
УЧЕБНОЕ ПОСОБИЕ
САМАРА 1998
УДК 519.2 (075)
Статистический анализ временных рядов авторегрессии и скользящего среднего : Учебное пособие / А.Ф.Тараскин; Самар. гос. аэрокосм. ун-т. Самара, 1998. 64 с.
ISBN 5-230-16 956-7
Кратко излагаются основные факты теории случайных временных рядов авторегрессии и скользящего среднего. Рассматривается статистические задачи для процессов при условии их стационарности.
Предназначено для студентов специальности «Прикладная математика» при изучении курса «Случайные процессы» и при выполнению курсовой работы по этому курсу. Подготовлено на кафедре «Техническая кибернетика».
Ил.2 Библиогр.: 7 назв. Табл 1.
Печатается по решению редакционно-издательского совета
Самарского государственного аэрокосмического университета
имени академика С.П.Королева
Рецензенты: А.И.Жданов, В.М.Климкин
ISBN 5-230-16 956-7 © Тараскин А.Ф., 1998
© Самарский государственный
аэрокосмический университет, 1998
ОГЛАВЛЕНИЕ
1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ....................................................... 4
1.1.Основные понятия и терминология........................................... 4
1.2.Элементы теории стационарных случайных процессов......... 5
2. ПРОЦЕССЫ АВТОРЕГРЕССИИ И СКОЛЬЗЯЩЕГО СРЕДНЕГО.. 7
2.1.Значение процессов авторегрессии
и скользящего среднего........................................................................ 7
2.2.Случайные последовательности авторегрессии....................... 7
2.3.Случайные последовательности скользящего среднего........ 13
2.4.Смешанная модель авторегрессии -
скользящего среднего......................................................................... 16
3. СТАТИСТИЧЕСКИЕ ВЫВОДЫ ПО НАБЛЮДЕНИЯМ
СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ...................................... 20
3.1.Общая характеристика задач статистики
и случайных процессов...................................................................... 20
3.2.Оценка среднего значения и корреляционной модели.......... 21
3.3.Оценивание параметров модели методом моментов............. 28
3.4.Оценивание параметров модели
методом максимального правдоподобия......................................... 32
Библиографический список.............................................................................. 48
Приложения...................................................................................................... 49
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Основные понятия и терминология
При исследовании реальных устройств, функционирующих в условиях случайных возмущений, экспериментатор может наблюдать и фиксировать реализации случайных процессов, связанных с работой устройства. При этом статистические закономерности процессов и параметры исследуемого устройства частично или полностью оказываются априори неизвестными. Поскольку получение точных значений интересующих характеристик и параметров, как правило, бывает невозможным, приходится оценивать из на основе обработки экспериментальных данных с учетом априорной информации, указывающей, например, класс к которому принадлежит исследуемый процесс.
Для широкого класса устройств модель функционирования может быть представлена как реакция на входные возмущения и начальное состояние. Модель, описывающую работу устройств как преобразование входных возмущений и начального состояния в выходную реакцию, называют системой.
Для математического описания системы удобно использовать принятую терминологию: так, входные возмущения и начальное состояние называют входным сигналом, реакцию системы - выходным сигналом. Входные и выходные сигналы в общем случае являются элементами произвольных пространств. Например, для механических устройств входными сигналами могут быть силы и моменты, а выходными - перемещения, скорости и ускорения. Для радиотехнических и электронных систем входными сигналами являются электромагнитные поля, токи и напряжения, а выходными - сигналы той же природы или звуковые сигналы, а возможно и телевизионные изображения. Для организационных систем в качестве входных сигналов можно рассматривать проблемы, а качестве выходных - решения проблем.
Обозначая входной сигнал через X, а выходной - через Y, можно схематически изобразить систему (рис.1).
Мы будем рассматривать стационарные (установившиеся) режимы функционирования систем, а это означает, что входной и
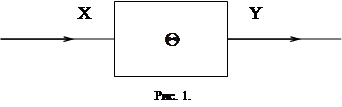
выходной процессы являются стационарными в широком смысле. Кроме этого, предположим, что X и Y, являются процессами с целочисленным временем: 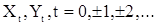 Такие процессы чаше называются случайными последовательностями (с.п.) или временными рядами.
Такие процессы чаше называются случайными последовательностями (с.п.) или временными рядами.
Случайных процессов
С.п. 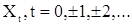 ., принимающая, вообще говоря, комплексные значения, называется стационарной в широком смысле, если для любого целого t
., принимающая, вообще говоря, комплексные значения, называется стационарной в широком смысле, если для любого целого t 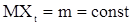 и корреляционная функция
и корреляционная функция
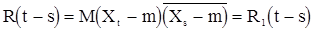
зависит только от разности моментов времени t и s. Таким образом, корреляционная функция стационарной с.п. является комплекснозначной функцией целочисленного аргумента:
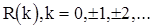
Она обладает следующими свойствами:
а.) 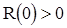 ; если же
; если же 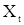 принимает только вещественные значения, то
принимает только вещественные значения, то 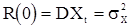 ;
;
б.) 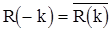 ; если
; если 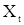 вещественнозначная с.п., то
вещественнозначная с.п., то 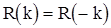 ;
;
в.) 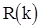 неотрицательно определена, т.е. для любого целого
неотрицательно определена, т.е. для любого целого 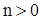 , любых целых
, любых целых 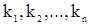 и любого набора комплексных чисел
и любого набора комплексных чисел 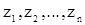 выполнятся неравенство
выполнятся неравенство
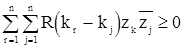
Согласно теореме А.Я.Хинчина для корреляционной функции стационарной с.п. имеет представление
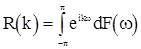 (1)
(1)
в котором 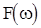 - неубывающая неотрицательная ограниченная функция на
- неубывающая неотрицательная ограниченная функция на 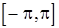 , называемая, как и в случае процессов с непрерывным временем, спектральной функцией. Если
, называемая, как и в случае процессов с непрерывным временем, спектральной функцией. Если
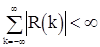 (2)
(2)
то функция 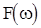 будет дифференцируемой, и она может быть представлена в виде
будет дифференцируемой, и она может быть представлена в виде
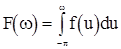 (3)
(3)
где 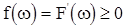 . При этом (1) можно заменить формулой
. При этом (1) можно заменить формулой
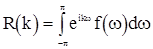 (4)
(4)
Функция 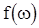 , где
, где 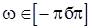 , называется спектральной плотностью случайной последовательности. Из (4) видно, что величины
, называется спектральной плотностью случайной последовательности. Из (4) видно, что величины 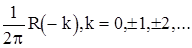 , являются коэффициентами Фурье функции
, являются коэффициентами Фурье функции 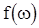 , так что разложение этой функции в ряд Фурье будет иметь вид
, так что разложение этой функции в ряд Фурье будет иметь вид
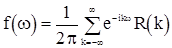 (5)
(5)
Эту формулу можно рассматривать как дискретный аналог известной формулы обращения для спектральной плотности непрерывного в среднем квадратическом (с.к.) стационарного в широком смысле процесса.
Используя теорему Карунена для стационарной последовательности 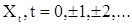 , с
, с 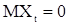 и с корреляционной функцией (1), получаем интегральное представление (теорема Хинчина)
и с корреляционной функцией (1), получаем интегральное представление (теорема Хинчина)
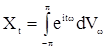 , (6)
, (6)
где в правой части имеем стохастический интеграл по процессу 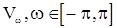 с ортогональными приращениями и со спектральной функцией
с ортогональными приращениями и со спектральной функцией 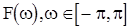 , совпадающей со спектральной функцией в представлении (1) корреляционной функции последовательности
, совпадающей со спектральной функцией в представлении (1) корреляционной функции последовательности 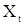 .
.
ПРОЦЕССЫ АВТОРЕГРЕССИИ
И СКОЛЬЗЯЩЕГО СРЕДНЕГО
И скользящего среднего
Разнообразные данные в физике, космических исследованиях, экономике, медицине и других областях поступают исследователю в виде случайных последовательностей (временных рядов). Совокупность существующих методов изучения таких рядов зависимых наблюдений называется анализом временных рядов.
В начале 70-х годов многие зарубежные исследователи стали аппроксимировать изучаемый временной ряд наиболее близкой (например, с точки зрения асимптотической среднеквадратичной теории) последовательностью авторегрессии, скользящего среднего или смешанной последовательностью авторегрессии - скользящего среднего. Это позволило характеризовать целый ряд наблюдений всего несколькими параметрами. Простота структуры последовательностей авторегрессии и скользящего среднего и в то же время возможность использования их для аппроксимации широкого класса с.п. определяют как практический, так и теоретический интерес к ним. Моделирование этих последовательностей позволяет решать самые разнообразные прикладные задачи, связанные с изучением реальных процессов в науке и технике.
Скользящего среднего
В теореме 1 утверждалось, что в условиях стационарности с.п.АР(p) 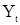 может быть представлена бесконечной линейной комбинацией с.в.
может быть представлена бесконечной линейной комбинацией с.в. 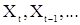 , т.е. может рассматриваться как с.п.СС(¥) с последовательностью параметров
, т.е. может рассматриваться как с.п.СС(¥) с последовательностью параметров 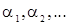 . Известно также, что и с.п.СС(q) может быть (при условии обратимости) представлена в виде с.п.АР(¥) с последовательностью параметров
. Известно также, что и с.п.СС(q) может быть (при условии обратимости) представлена в виде с.п.АР(¥) с последовательностью параметров 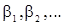 . Это ставит вопрос об экономичности (в смысле числа используемых параметров) представления данной с.п. На практике для получения экономичной параметризации иногда бывает необходимо включать в модель как члены, описывающие авторегрессию, так и члены, моделирующие скользящее среднее. Такая с.п. может определена уравнением
. Это ставит вопрос об экономичности (в смысле числа используемых параметров) представления данной с.п. На практике для получения экономичной параметризации иногда бывает необходимо включать в модель как члены, описывающие авторегрессию, так и члены, моделирующие скользящее среднее. Такая с.п. может определена уравнением
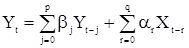 , (43)
, (43)
где 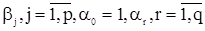 - вещественные параметры, а
- вещественные параметры, а 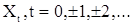 - последовательность некоррелированных одинаково распределенных с.в. с
- последовательность некоррелированных одинаково распределенных с.в. с 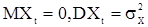 и называется смешанной с.п. авторегрессии-скользящего среднего порядка (p,q). В дальнейшем такую последовательность сокращенно будем обозначать АРСС(p,q).
и называется смешанной с.п. авторегрессии-скользящего среднего порядка (p,q). В дальнейшем такую последовательность сокращенно будем обозначать АРСС(p,q).
В соответствии с замечанием к теореме 1 члены со скользящим средним в правой части (43) не повлияют на условия стационарности последовательности 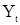 . Поэтому с.п. АРСС(p,q) будет стационарной в широком смысле при условии, что все корни характеристического уравнения
. Поэтому с.п. АРСС(p,q) будет стационарной в широком смысле при условии, что все корни характеристического уравнения
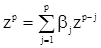 (44)
(44)
лежат внутри единичного круга 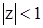 . Аналогично для обратимости АРСС(p,q) корни характеристического уравнения
. Аналогично для обратимости АРСС(p,q) корни характеристического уравнения
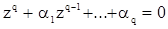 (45)
(45)
должны лежать внутри единичного круга 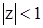 .
.
Предполагая с.п. АРСС(p,q) стационарной, найдем, как и для с.п. АР(p), рекуррентные соотношения, связывающие параметры 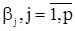 и
и 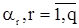 со значениями корреляционной функции. Для этого все члены в (43) умножим на
со значениями корреляционной функции. Для этого все члены в (43) умножим на 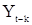 и, перейдя к математическим ожиданиям получаем
и, перейдя к математическим ожиданиям получаем
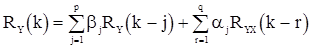 , (46)
, (46)
где 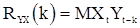 - взаимная корреляционная функция последовательностей X и Y. Так как
- взаимная корреляционная функция последовательностей X и Y. Так как 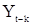 зависит только от членов входной последовательности X до момента
зависит только от членов входной последовательности X до момента 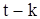 , то, очевидно, что
, то, очевидно, что 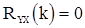 при
при 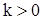 и
и 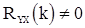 для
для 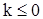 . Из (46) следует, что
. Из (46) следует, что
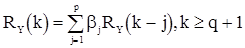 (47)
(47)
и для нормированной корреляционной функции
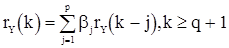 (47’)
(47’)
Это означает, что для с.п. АРСС(p,q) существует q значений корреляционной функции 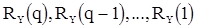 , которые связаны зависимостью (46) с q параметрами скользящего среднего
, которые связаны зависимостью (46) с q параметрами скользящего среднего 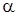 и p параметрами авторегрессии
и p параметрами авторегрессии 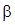 . Для решения разностных уравнений (47) и (47’) (для больших k) в качестве начальных необходимы p значений, например,
. Для решения разностных уравнений (47) и (47’) (для больших k) в качестве начальных необходимы p значений, например, 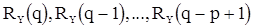 .
.
Дисперсию с.п. АРСС(p,q) 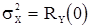 вместе с
вместе с 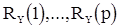 получим, решая систему уравнений, получающаяся из (46) при k=0,1,2,...,p.
получим, решая систему уравнений, получающаяся из (46) при k=0,1,2,...,p.
Спектральную плотность можно получить аналогично случаям «чистых» последовательностей АР(p) и СС(q).
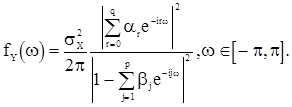 (48)
(48)
Рассмотрим подробнее случай АРСС(2,1):
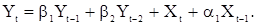 (49)
(49)
Из (46) имеем
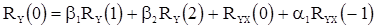 (50)
(50)
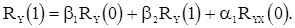 (51)
(51)
Чтобы найти 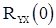 и
и 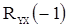 , умножим поочередно (49) на
, умножим поочередно (49) на 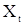 и
и 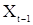 и перейдем к математическим ожиданиям. В результате получим
и перейдем к математическим ожиданиям. В результате получим
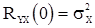 и
и 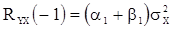 .
.
Тогда уравнениям (50) и (51) приобретают вид
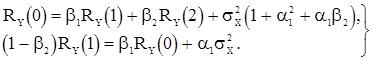 (52)
(52)
При 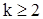
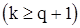 уравнения (47) в рассматриваемом случае имеют вид
уравнения (47) в рассматриваемом случае имеют вид
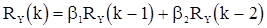 (53)
(53)
и вместе с уравнениями (52) позволяют определить последовательность 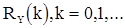 . В частности, из системы уравнений (52) и уравнения (53) при
. В частности, из системы уравнений (52) и уравнения (53) при 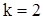 получаем формулу для дисперсии
получаем формулу для дисперсии
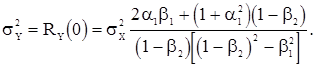 (54)
(54)
Спектральная плотность с.п. АРСС(2,1) согласно (48) имеет вид
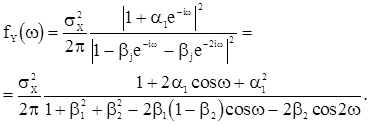 (55)
(55)
Наконец, рассмотрим часто употребляемую в различных прикладных науках с.п. АРСС(1,1). Она определяются разностным уравнением
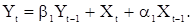 (56)
(56)
В этом случае входящая в с.п. авторегрессия имеет порядок p=1, и корень ее характеристического уравнения равен 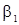 . Последова-тельность будет стационарной, если
. Последова-тельность будет стационарной, если 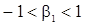 . Уравнения для корреляционной функции получаются из формул (46) и (47)
. Уравнения для корреляционной функции получаются из формул (46) и (47)
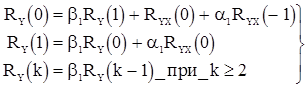 (57)
(57)
Выражения для 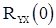 и
и 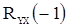 получаются аналогично предыдущему умножением (56) на
получаются аналогично предыдущему умножением (56) на 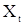 и
и 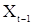 и переходом к математическим ожиданиям.
и переходом к математическим ожиданиям.
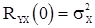 ,
,
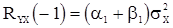 . (58)
. (58)
Из (57) и (58) получаем выражения корреляционной функции с.п. АРСС(1,1)
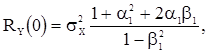
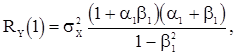 (59)
(59)
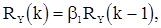
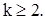
Из (59) следует, что при 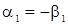 имеем
имеем 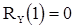 . Поэтому
. Поэтому 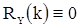 при всех значениях
при всех значениях 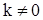 , т.е. последовательность
, т.е. последовательность 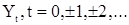 является некоррелированной.
является некоррелированной.
Спектральная плотность с.п. АРСС(1,1) будет иметь вид
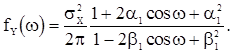 (60)
(60)
СЛУЧАЙНЫХ ВЕРОЯТНОСТЕЙ
Общая характеристика задач
Оценка среднего значения
И корреляционной функции
Пусть 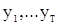 - T последовательных наблюдений с.п.
- T последовательных наблюдений с.п. 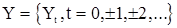 , стационарной в широком смысле со средним значением
, стационарной в широком смысле со средним значением 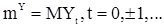 , и корреляционной функцией
, и корреляционной функцией 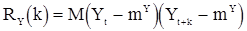 ,
, 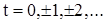 ,
, 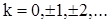 ,
, 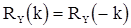 .
.
Рассмотрим сначала оценивание среднего значения 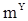 . Будем искать оценку величины
. Будем искать оценку величины 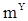 в классе линейных оценок, т.е. среди линейных комбинаций наблюдений
в классе линейных оценок, т.е. среди линейных комбинаций наблюдений
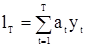 . (63)
. (63)
Среднее значение и дисперсия произвольной линейной комбинации (63) соответственно равны
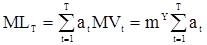 (64)
(64)
и
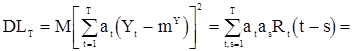
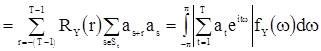 , (65)
, (65)
где 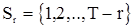 при
при 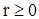 и
и 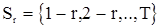 при
при 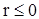 . Для того, чтобы с.в.
. Для того, чтобы с.в. 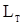 была несмещенной оценкой среднего значения
была несмещенной оценкой среднего значения 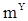 , должно выполнятся равенство
, должно выполнятся равенство
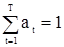 (66)
(66)
По обычным правилам отыскания условного экстремума находим вектор 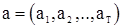 , обеспечивающий минимальную дисперсию несмещенной оценке
, обеспечивающий минимальную дисперсию несмещенной оценке
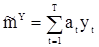 ,
, 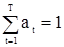 . (67)
. (67)
Несложные выкладки показывают, что несмещенная линейная оценка с минимальной дисперсией задается формулой (67) при векторе коэффициентов
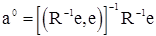 , (68)
, (68)
где 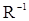 - матрица, обратная к корреляционной матрице наблюдений
- матрица, обратная к корреляционной матрице наблюдений 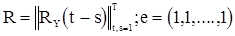 - единичный вектор, а (.,.) - скалярное произведение n-мерном евклидовом пространстве. Таким образом, оптимальная линейная несмещенная оценка будет иметь вид
- единичный вектор, а (.,.) - скалярное произведение n-мерном евклидовом пространстве. Таким образом, оптимальная линейная несмещенная оценка будет иметь вид
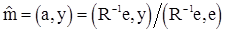 . (69)
. (69)
где 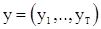 - вектор наблюдений, а дисперсия этой оценки определяется равенством
- вектор наблюдений, а дисперсия этой оценки определяется равенством
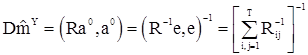 (70)
(70)
где 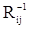 - элементы матрицы
- элементы матрицы 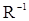 .
.
На практике часто в качестве несмещенной оценки среднего значения стационарной с.п. используется среднее арифметическое наблюдений
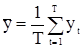 (71)
(71)
Используя формулу (65) получим дисперсию этой оценки
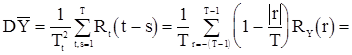
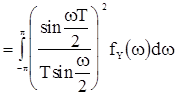 . (72)
. (72)
Асимптотическое (при 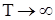 ) поведение дисперсии среднеарифметической оценки величины
) поведение дисперсии среднеарифметической оценки величины 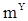 дается следующей теоремой.
дается следующей теоремой.
Теорема 3. Если выполняется условие
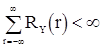 , (73)
, (73)
то оценка (71) состоятельна и
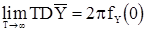 . (74)
. (74)
Доказательство состоятельности оценки 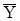 следует из того, что при условии (73)
следует из того, что при условии (73) 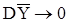 при
при 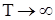 . Основанием соотношения (74) является известный из анализа факт.
. Основанием соотношения (74) является известный из анализа факт.
Лемма. Если ряд 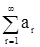 сходится, то
сходится, то
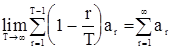 . (75)
. (75)
Соотношение (75) следует из (74), если учесть разложение вида (5) спектральной плотности в ряд Фурье, полагая в нем 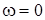 .
.
Теперь рассмотрим оценивание корреляционной функции. Если 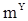 известно, то обычно используется оценка
известно, то обычно используется оценка
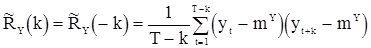 , (76)
, (76)
где 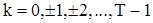 .
.
Если 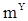 неизвестно, то по аналогии можно построить следующую оценку:
неизвестно, то по аналогии можно построить следующую оценку:
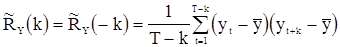 , (77)
, (77)
где 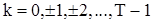 .
.
Возможны еще и другие оценки, в частности
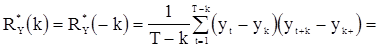
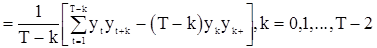 ,
,
где
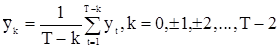 ,
,
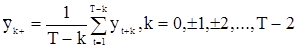 .
.
Рассмотрим моменты первого и второго порядков оценок величины 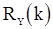 . Непосредственные вычисления дают следующие результаты. В случае известного среднего
. Непосредственные вычисления дают следующие результаты. В случае известного среднего 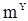
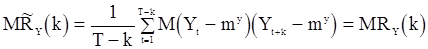 , (78)
, (78)
т.е. оценка 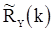 является несмещенной. В случае неизвестного
является несмещенной. В случае неизвестного 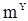 для математического ожидания оценки
для математического ожидания оценки 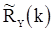 после несложных, но утомительных вычислений получаем соотношения:
после несложных, но утомительных вычислений получаем соотношения:
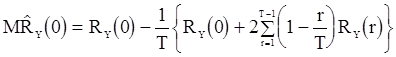 ; (79)
; (79)
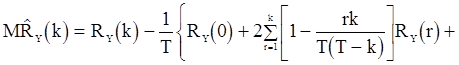
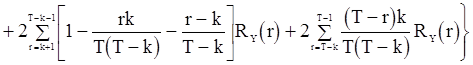 (80)
(80)
если 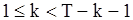 ;
;
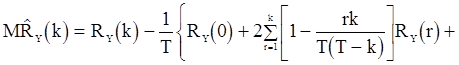
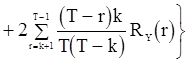 , (81)
, (81)
если 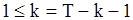 ;
;
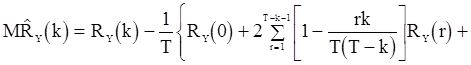
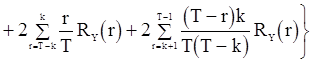 , (82)
, (82)
если 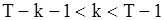 ;
;
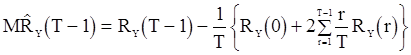 . (83)
. (83)
Формулы (79)-(83) показывают, что оценка 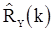 является смещенной, порядок смещения равен
является смещенной, порядок смещения равен 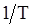 .
.
Математическое ожидание оценки 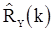 можно также выразить с помощью спектральной плотности
можно также выразить с помощью спектральной плотности
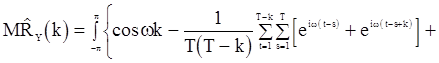
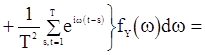
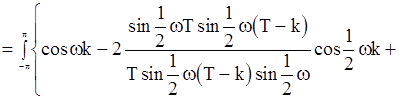
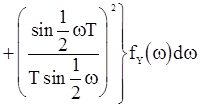 . (84)
. (84)
Аналогичные выражения можно получить и для математического ожидания оценки 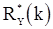 .
.
Ждя дисперсии несмещенной оценки 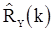 можно получить следующее выражение:
можно получить следующее выражение:
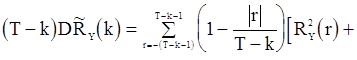
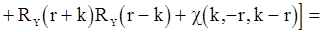
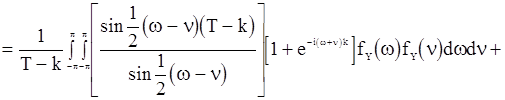
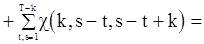
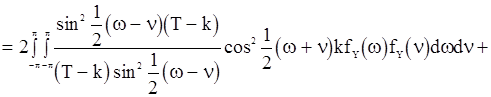
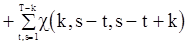
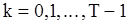 , (85)
, (85)
где 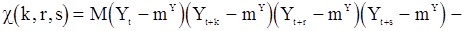
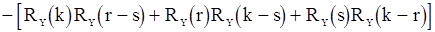 - семиинвариант четвертого порядка.
- семиинвариант четвертого порядка.
Если последовательность 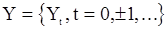 гауссовская, то семиинварианты четвертого порядка в выражениях (85) обращаются в нуль.
гауссовская, то семиинварианты четвертого порядка в выражениях (85) обращаются в нуль.
Более трудоемко вычисление выражений для дисперсий смещенных оценок 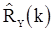 и
и 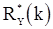 ; сами выражения дисперсий более громоздки и мы их не приводим.
; сами выражения дисперсий более громоздки и мы их не приводим.
Отметим некоторые ассимптотические свойства оценок корреляционоой функции. При известном среднем 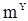 оценка
оценка 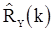 , как уже отмечалось выше, является несмещенной. При неизвестном среднем оценки
, как уже отмечалось выше, является несмещенной. При неизвестном среднем оценки 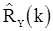 и
и 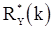 , как показывают, в частности, формулы (79)-(83), являются смещенными, причем смещение содержит множитель
, как показывают, в частности, формулы (79)-(83), являются смещенными, причем смещение содержит множитель 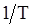 . Более точно поведение оценок
. Более точно поведение оценок 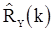 и
и 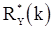 при
при 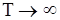 выражается следующей теоремой.
выражается следующей теоремой.
Теорема 4. Если 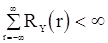 , то оценки
, то оценки 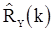 и
и 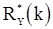 являются ассимптотическими несмещенными и
являются ассимптотическими несмещенными и
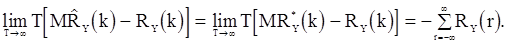 Если
Если 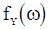 непрерывна при
непрерывна при 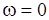 , то
, то
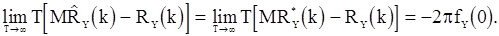
Вернемся к дисперсиям оценок корреляционной функции. Если для с.п. 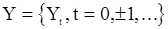 ,
, 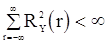 и
и 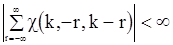 , то предельная дисперсия величины
, то предельная дисперсия величины 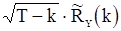 будет определятся соотношением
будет определятся соотношением
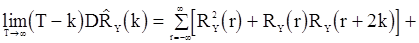
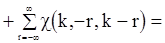
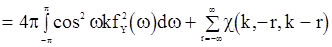 . (86)
. (86)
Соотношение (86) вместе с асимптотической несмещенностью означают состоятельность оценки 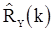 .
.
Если 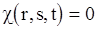 (что имеет место для гауссовских с.п.) и
(что имеет место для гауссовских с.п.) и 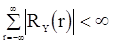 , то предельные дисперсии величин
, то предельные дисперсии величин 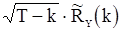 стремятся к
стремятся к 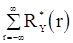 , когда
, когда 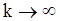 .
.
Можно установить, что если моменты с.п. 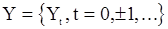 до четвертого порядка включительно соответствуют стационарности, и
до четвертого порядка включительно соответствуют стационарности, и
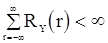 и
и 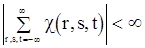 ,
,
то разность между 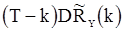 и
и 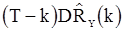 , а также между
, а также между 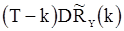 и
и 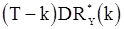 имеет порядок
имеет порядок 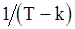 . Это означает, во-первых, что оценки
. Это означает, во-первых, что оценки 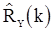 и
и 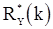 состоятельны, а, во-вторых, что для «больших выборок» величину
состоятельны, а, во-вторых, что для «больших выборок» величину 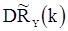 можно использовать как апроксимацию для
можно использовать как апроксимацию для 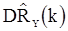 и
и 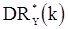 .
.
Методом моментов
Одним из общих методов нахождения оценок параметров является метод моментов. Он заключается в приравнивании определенного количества выборочных моментов к соответствующим теоретическим параметрам, которые являются функциями от неизвестных параметров. Рассматривая количество моментов, равное числу оцениваемых параметров, получаем искомые оценки. На практике этод метод приводит к сравнительно простым вычислениям. Мы рассмотрим применение этого метода последовательно к оцениванию параметров последовательности АР(p), СС(q) и АРСС(p,q).
Для уравнений с.п.АР(p) метод моментов сводится к решению системы уравнений Юла-Уокера (11) для 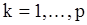 относительно параметров
относительно параметров 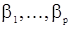 . Вместо теоретических значений корреляционной функции
. Вместо теоретических значений корреляционной функции 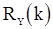 следует подставить их оценки. В качестве таких оценок можно использовать
следует подставить их оценки. В качестве таких оценок можно использовать 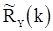 ,
, 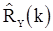 и
и 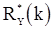 из предыдущего раздела. Поскольку эти оценки состоятельны, то при больших T с вероятностью, близкой к единице, выборочная корреляционная матрица будет невырожденной и уравнения Юла-Уокера будут иметь решение
из предыдущего раздела. Поскольку эти оценки состоятельны, то при больших T с вероятностью, близкой к единице, выборочная корреляционная матрица будет невырожденной и уравнения Юла-Уокера будут иметь решение 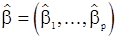 , которое будет также состоятельной оценкой вектора
, которое будет также состоятельной оценкой вектора 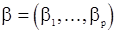 . Однако оценки, найденные с помощью метода моментов, с точки зрения эффективности не являются наилучшими из возможных и даже при больших T они имеют наименьшую возможную дисперсию. В рассматриваемой модели с.п.АР(p) дисперсия «шума»
. Однако оценки, найденные с помощью метода моментов, с точки зрения эффективности не являются наилучшими из возможных и даже при больших T они имеют наименьшую возможную дисперсию. В рассматриваемой модели с.п.АР(p) дисперсия «шума» 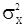 тоже может являтся неизвестным параметром и для ее оценки может быть использованно равенство (14), в котором значения
тоже может являтся неизвестным параметром и для ее оценки может быть использованно равенство (14), в котором значения 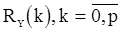 следует заменить их оценками, как при оценивании
следует заменить их оценками, как при оценивании 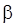 , а сами параметры
, а сами параметры 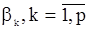 в (14) должны быть заменены уже найденными оценками
в (14) должны быть заменены уже найденными оценками 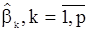 .
.
Приведем два примера оценок, полученных по методу моментов.
1. Последовательность АР(1), определяемая уравнением (8), содержит один неизвестный параметр 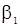 . Уравнение Юла-Уокера имеет вид
. Уравнение Юла-Уокера имеет вид 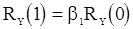 . Подставляя в него вместо
. Подставляя в него вместо 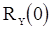 и
и 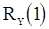 оценки
оценки 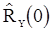 и
и 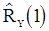 вида (77), получаем
вида (77), получаем
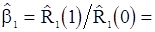
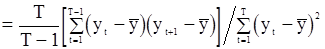 . (87)
. (87)
В нашем примере равенство (14) имеет вид
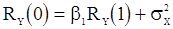 .
.
Отсюда получается оценка дисперсии «шума»
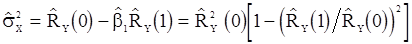 .
.
2. Последовательность АР(2), определяемая уравнением (9), содержит неизвестные параметр 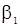 и
и 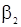 . Система уравнений Юла-Уокера имеет вид
. Система уравнений Юла-Уокера имеет вид
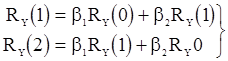
и дает оценки
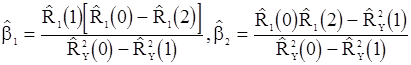 .
.
Оценка для дисперсии «шума» 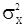 будет иметь вид
будет иметь вид
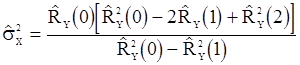 ,
,
В случае последовательности СС(q) метод моментов приводит к системе нелинейных уравнений относительно параметров 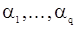 , если в (33) полагать
, если в (33) полагать 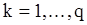 . Два метода решения такой нелинейной системы изложены в [3, с.226-229]. Приведем здесь один из них. Это так называемый линейно сходящийся итеративный процесс.
. Два метода решения такой нелинейной системы изложены в [3, с.226-229]. Приведем здесь один из них. Это так называемый линейно сходящийся итеративный процесс.
Из выражений (34) и (33) для корреляционной функции процесса СС(q) можно найти оценки параметров 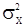 ,
, 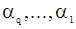 точно в том порядке, как здесь указано, при помощи итераций
точно в том порядке, как здесь указано, при помощи итераций
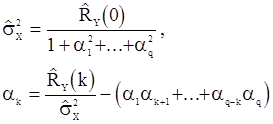 (88)
(88)
с условием, что 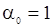 . Параметры
. Параметры 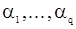 приравниваются к нулю в самом начале итеративной процедуры; значения
приравниваются к нулю в самом начале итеративной процедуры; значения 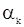 и
и 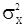 , используемые в любом цикле вычисления - это последние из доступных оценок этих величин. Например, в случае
, используемые в любом цикле вычисления - это последние из доступных оценок этих величин. Например, в случае 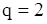 уравнения (88) имеют вид
уравнения (88) имеют вид
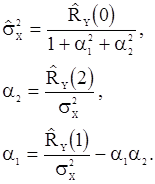
В случае  уравнения (88) приобретают вид
уравнения (88) приобретают вид
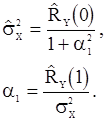
После исключения из этих уравнений величины 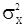 приходим к квадратному уравнению относительно
приходим к квадратному уравнению относительно 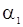 и находим оценку
и находим оценку
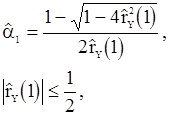 (89)
(89)
в которой 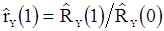 . Затем получаем оценку
. Затем получаем оценку
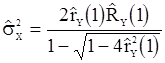 . (90)
. (90)
Наконец, рассмотрим оценку параметров в смешанной модели АРСС(p,q). Для оценки параметров авторегрессии 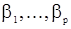 можно использовать p-уравнения вида (47) для
можно использовать p-уравнения вида (47) для 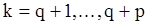 , в которых значения корреляционной функции
, в которых значения корреляционной функции 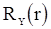 заменяются выборочными значениями (оценками). Затем введем вспомогательный процесс W, полагая
заменяются выборочными значениями (оценками). Затем введем вспомогательный процесс W, полагая
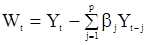 ,
, 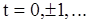 (91)
(91)
Тогда уравнению (43) можно придать вид
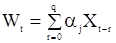
и, следовательно, с.п.W можно рассматривать как «чистую» последовательность CC(q). Исходя из равенства (91), можно выразить корреляционную функцию последовательности W через значения корреляционной функции последовательности Y. Можно показать, что
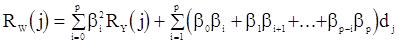 , (92)
, (92)
где 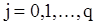 ;
; 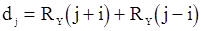 ,
, 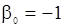 .
.
Далее, пользуясь уже найдеными оценками для 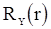 и параметров
и параметров 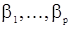 , по формулам (92) будем иметь оценки для корреляционной функции
, по формулам (92) будем иметь оценки для корреляционной функции 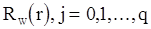 . На заключительном этапе используем описанный выше линейно сходящийся итеративный процесс для оценки неизвестных
. На заключительном этапе используем описанный выше линейно сходящийся итеративный процесс для оценки неизвестных 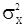 ,
, 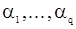 либо (в частном случае
либо (в частном случае 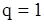 ) воспользуемся готовыми формулами (89) и (90), в которых оценки
) воспользуемся готовыми формулами (89) и (90), в которых оценки 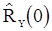 и
и 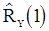 должны быть заменены оценками
должны быть заменены оценками 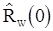 и
и 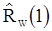 .
.
Оценивание параметров
СТАТИСТИЧЕСКИЙ АНАЛИЗ
ВРЕМЕННЫХ РЯДОВ
АВТОРЕГРЕССИИ
И СКОЛЬЗЯЩЕГО СРЕДНЕГО
УЧЕБНОЕ ПОСОБИЕ
САМАРА 1998
УДК 519.2 (075)
Статистический анализ временных рядов авторегрессии и скользящего среднего : Учебное пособие / А.Ф.Тараскин; Самар. гос. аэрокосм. ун-т. Самара, 1998. 64 с.
ISBN 5-230-16 956-7
Кратко излагаются основные факты теории случайных временных рядов авторегрессии и скользящего среднего. Рассматривается статистические задачи для процессов при условии их стационарности.
Предназначено для студентов специальности «Прикладная математика» при изучении курса «Случайные процессы» и при выполнению курсовой работы по этому курсу. Подготовлено на кафедре «Техническая кибернетика».
Ил.2 Библиогр.: 7 назв. Табл 1.
Печатается по решению редакционно-издательского совета
Самарского государственного аэрокосмического университета
имени академика С.П.Королева
Рецензенты: А.И.Жданов, В.М.Климкин
ISBN 5-230-16 956-7 © Тараскин А.Ф., 1998
© Самарский государственный
аэрокосмический университет, 1998
ОГЛАВЛЕНИЕ
1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ....................................................... 4
1.1.Основные понятия и терминология........................................... 4
1.2.Элементы теории стационарных случайных процессов......... 5
2. ПРОЦЕССЫ АВТОРЕГРЕССИИ И СКОЛЬЗЯЩЕГО СРЕДНЕГО.. 7
2.1.Значение процессов авторегрессии
и скользящего среднего........................................................................ 7
2.2.Случайные последовательности авторегрессии....................... 7
2.3.Случайные последовательности скользящего среднего........ 13
2.4.Смешанная модель авторегрессии -
скользящего среднего......................................................................... 16
3. СТАТИСТИЧЕСКИЕ ВЫВОДЫ ПО НАБЛЮДЕНИЯМ
СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ...................................... 20
3.1.Общая характеристика задач статистики
и случайных процессов...................................................................... 20
3.2.Оценка среднего значения и корреляционной модели.......... 21
3.3.Оценивание параметров модели методом моментов............. 28
3.4.Оценивание параметров модели
методом максимального правдоподобия......................................... 32
Библиографический список.............................................................................. 48
Приложения...................................................................................................... 49
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Основные понятия и терминология
При исследовании реальных устройств, функционирующих в условиях случайных возмущений, экспериментатор может наблюдать и фиксировать реализации случайных процессов, связанных с работой устройства. При этом статистические закономерности процессов и параметры исследуемого устройства частично или полностью оказываются априори неизвестными. Поскольку получение точных значений интересующих характеристик и параметров, как правило, бывает невозможным, приходится оценивать из на основе обработки экспериментальных данных с учетом априорной информации, указывающей, например, класс к которому принадлежит исследуемый процесс.
Для широкого класса устройств модель функционирования может быть представлена как реакция на входные возмущения и начальное состояние. Модель, описывающую работу устройств как преобразование входных возмущений и начального состояния в выходную реакцию, называют системой.
Для математического описания системы удобно использовать принятую терминологию: так, входные возмущения и начальное состояние называют входным сигналом, реакцию системы - выходным сигналом. Входные и выходные сигналы в общем случае являются элементами произвольных пространств. Например, для механических устройств входными сигналами могут быть силы и моменты, а выходными - перемещения, скорости и ускорения. Для радиотехнических и электронных систем входными сигналами являются электромагнитные поля, токи и напряжения, а выходными - сигналы той же природы или звуковые сигналы, а возможно и телевизионные изображения. Для организационных систем в качестве входных сигналов можно рассматривать проблемы, а качестве выходных - решения проблем.
Обозначая входной сигнал через X, а выходной - через Y, можно схематически изобразить систему (рис.1).
Мы будем рассматривать стационарные (установившиеся) режимы функционирования систем, а это означает, что входной и
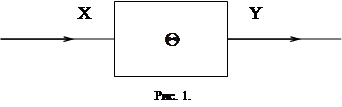
выходной процессы являются стационарными в широком смысле. Кроме этого, предположим, что X и Y, являются процессами с целочисленным временем: 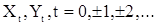 Такие процессы чаше называются случайными последовательностями (с.п.) или временными рядами.
Такие процессы чаше называются случайными последовательностями (с.п.) или временными рядами.
Элементы теории стационарных
Случайных процессов
С.п. 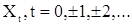 ., принимающая, вообще говоря, комплексные значения, называется стационарной в широком смысле, если для любого целого t
., принимающая, вообще говоря, комплексные значения, называется стационарной в широком смысле, если для любого целого t 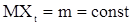 и корреляционная функция
и корреляционная функция
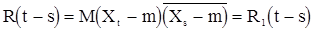
зависит только от разности моментов времени t и s. Таким образом, корреляционная функция стационарной с.п. является комплекснозначной функцией целочисленного аргумента:
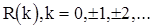
Она обладает следующими свойствами:
а.) 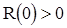 ; если же
; если же 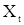 принимает только вещественные значения, то
принимает только вещественные значения, то 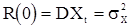 ;
;
б.) 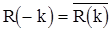 ; если
; если 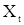 вещественнозначная с.п., то
вещественнозначная с.п., то 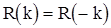 ;
;
в.) 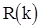 неотрицательно определена, т.е. для любого целого
неотрицательно определена, т.е. для любого целого 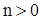 , любых целых
, любых целых 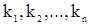 и любого набора комплексных чисел
и любого набора комплексных чисел 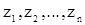 выполнятся неравенство
выполнятся неравенство
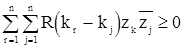
Согласно теореме А.Я.Хинчина для корреляционной функции стационарной с.п. имеет представление
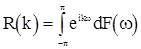 (1)
(1)
в котором 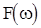 - неубывающая неотрицательная ограниченная функция на
- неубывающая неотрицательная ограниченная функция на 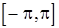 , называемая, как и в случае процессов с непрерывным временем, спектральной функцией. Если
, называемая, как и в случае процессов с непрерывным временем, спектральной функцией. Если
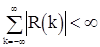 (2)
(2)
то функция 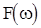 будет дифференцируемой, и она может быть представлена в виде
будет дифференцируемой, и она может быть представлена в виде
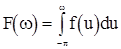 (3)
(3)
где 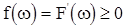 . При этом (1) можно заменить формулой
. При этом (1) можно заменить формулой
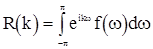 (4)
(4)
Функция 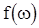 , где
, где 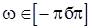 , называется спектральной плотностью случайной последовательности. Из (4) видно, что величины
, называется спектральной плотностью случайной последовательности. Из (4) видно, что величины 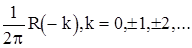 , являются коэффициентами Фурье функции
, являются коэффициентами Фурье функции 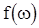 , так что разложение этой функции в ряд Фурье будет иметь вид
, так что разложение этой функции в ряд Фурье будет иметь вид
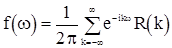 (5)
(5)
Эту формулу можно рассматривать как дискретный аналог известной формулы обращения для спектральной плотности непрерывного в среднем квадратическом (с.к.) стационарного в широком смысле процесса.
Используя теорему Карунена для стационарной последовательности 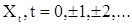 , с
, с 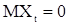 и с корреляционной функцией (1), получаем интегральное представление (теорема Хинчина)
и с корреляционной функцией (1), получаем интегральное представление (теорема Хинчина)
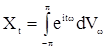 , (6)
, (6)
где в правой части имеем стохастический интеграл по процессу 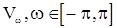 с ортогональными приращениями и со спектральной функцией
с ортогональными приращениями и со спектральной функцией 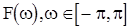 , совпадающей со спектральной функцией в представлении (1) корреляционной функции последовательности
, совпадающей со спектральной функцией в представлении (1) корреляционной функции последовательности 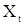 .
.
ПРОЦЕССЫ АВТОРЕГРЕССИИ
И СКОЛЬЗЯЩЕГО СРЕДНЕГО
Дата: 2019-04-23, просмотров: 352.