Последовательность с.в. 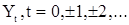 называют случайной последовательностью скользящего среднего порядка
называют случайной последовательностью скользящего среднего порядка 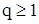 (с.п.СС(q)), если она задается равенством
(с.п.СС(q)), если она задается равенством
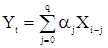 (32)
(32)
в котором 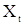 - последовательность вещественных некоррелированных и одинаково распределенных с
- последовательность вещественных некоррелированных и одинаково распределенных с 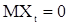 и
и 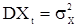 с.в., а
с.в., а 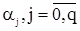
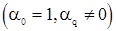 - вещественные параметры. Из определения с.п.СС(q) следует, что
- вещественные параметры. Из определения с.п.СС(q) следует, что 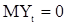 . Вычислим ее корреляционную функцию
. Вычислим ее корреляционную функцию
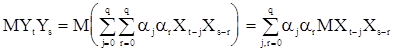 .
.
Так как 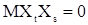 при
при 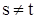 и
и 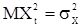 , то в сумме в правой части последнего неравенства ненулевыми будут только слагаемые, индексы которых удовлетворяют равенству
, то в сумме в правой части последнего неравенства ненулевыми будут только слагаемые, индексы которых удовлетворяют равенству 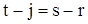 или
или 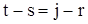 . Если
. Если 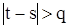 , то все слагаемые в сумме нулевые. При
, то все слагаемые в сумме нулевые. При 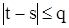
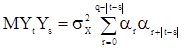 .
.
Итак, с.п.СС(q) оказывается стационарной в широком смысле без всяких ограничений на параметры 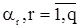 . Обозначая ее корреляционную функцию через
. Обозначая ее корреляционную функцию через 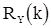 , получаем формулу
, получаем формулу
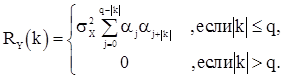 (33)
(33)
Для с.п.СС(q) отсюда имеем формулу
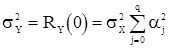 . (34)
. (34)
Условие (2) для корреляционной функции (33), очевидно, выполняется и, следовательно, существует спектральная плотность с.п.СС(q), которую обозначим  . Спектральная плотность «входной» последовательности
. Спектральная плотность «входной» последовательности  согласно (16) постоянна на
согласно (16) постоянна на 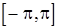 и
и 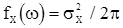 . С.в.
. С.в. 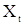 имеет интегральное представление (6). В соответствии с теоремой Хинчина «выходная» последовательность
имеет интегральное представление (6). В соответствии с теоремой Хинчина «выходная» последовательность 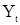 будет иметь представление вида (17). Учитывая эти представления, равенство (32) можно записать в виде
будет иметь представление вида (17). Учитывая эти представления, равенство (32) можно записать в виде
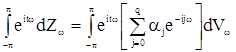 .
.
Умножим это равенство на такое же равенство, в котором вместо t положено 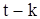 , и в обеих частях произведен переход к комплексно-сопряженным величинам. Беря затем математические ожидания от обеих частей полученного равенства, находим
, и в обеих частях произведен переход к комплексно-сопряженным величинам. Беря затем математические ожидания от обеих частей полученного равенства, находим
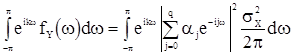 .
.
Из единственности интегрального представления корреляционной функции отсюда имеем
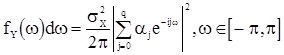 . (35)
. (35)
Оказывается, что спектральная плотность с.п.СС(q), вообще говоря, неоднозначно определятся параметрами 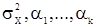 . Во избежание этого достаточно условится, чтобы корни характеристического уравнения
. Во избежание этого достаточно условится, чтобы корни характеристического уравнения
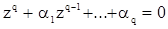 (36)
(36)
лежали, например, внутри единичного круга. Это условие однозначности иногда в литературе называется условием обратимости с.п.СС(q).
Большое практическое применение имеют последовательности скользящего среднего первого и второго порядков. с.п.СС(1) определяются уравнением
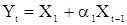 , (37)
, (37)
и ее корреляционная функция имеет вид
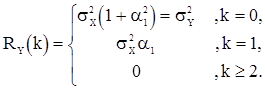 (38)
(38)
Спектральная плотность с.п.СС(1) имеет вид
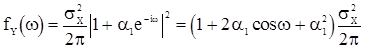 . (39)
. (39)
С.п.СС(2) определяется уравнением
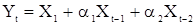 , (40)
, (40)
а ее корреляционная имеет вид
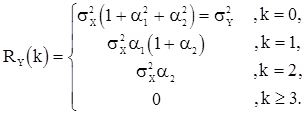 (41)
(41)
Спектральная плотность с.п.СС(2) имеет вид
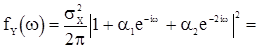
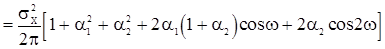 . (42)
. (42)
Смешанная модель авторегрессии -
Скользящего среднего
В теореме 1 утверждалось, что в условиях стационарности с.п.АР(p) 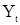 может быть представлена бесконечной линейной комбинацией с.в.
может быть представлена бесконечной линейной комбинацией с.в. 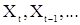 , т.е. может рассматриваться как с.п.СС(¥) с последовательностью параметров
, т.е. может рассматриваться как с.п.СС(¥) с последовательностью параметров 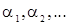 . Известно также, что и с.п.СС(q) может быть (при условии обратимости) представлена в виде с.п.АР(¥) с последовательностью параметров
. Известно также, что и с.п.СС(q) может быть (при условии обратимости) представлена в виде с.п.АР(¥) с последовательностью параметров 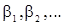 . Это ставит вопрос об экономичности (в смысле числа используемых параметров) представления данной с.п. На практике для получения экономичной параметризации иногда бывает необходимо включать в модель как члены, описывающие авторегрессию, так и члены, моделирующие скользящее среднее. Такая с.п. может определена уравнением
. Это ставит вопрос об экономичности (в смысле числа используемых параметров) представления данной с.п. На практике для получения экономичной параметризации иногда бывает необходимо включать в модель как члены, описывающие авторегрессию, так и члены, моделирующие скользящее среднее. Такая с.п. может определена уравнением
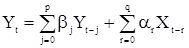 , (43)
, (43)
где 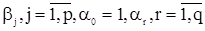 - вещественные параметры, а
- вещественные параметры, а 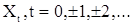 - последовательность некоррелированных одинаково распределенных с.в. с
- последовательность некоррелированных одинаково распределенных с.в. с 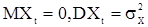 и называется смешанной с.п. авторегрессии-скользящего среднего порядка (p,q). В дальнейшем такую последовательность сокращенно будем обозначать АРСС(p,q).
и называется смешанной с.п. авторегрессии-скользящего среднего порядка (p,q). В дальнейшем такую последовательность сокращенно будем обозначать АРСС(p,q).
В соответствии с замечанием к теореме 1 члены со скользящим средним в правой части (43) не повлияют на условия стационарности последовательности 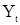 . Поэтому с.п. АРСС(p,q) будет стационарной в широком смысле при условии, что все корни характеристического уравнения
. Поэтому с.п. АРСС(p,q) будет стационарной в широком смысле при условии, что все корни характеристического уравнения
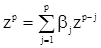 (44)
(44)
лежат внутри единичного круга 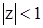 . Аналогично для обратимости АРСС(p,q) корни характеристического уравнения
. Аналогично для обратимости АРСС(p,q) корни характеристического уравнения
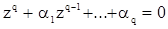 (45)
(45)
должны лежать внутри единичного круга 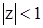 .
.
Предполагая с.п. АРСС(p,q) стационарной, найдем, как и для с.п. АР(p), рекуррентные соотношения, связывающие параметры 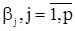 и
и 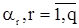 со значениями корреляционной функции. Для этого все члены в (43) умножим на
со значениями корреляционной функции. Для этого все члены в (43) умножим на 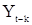 и, перейдя к математическим ожиданиям получаем
и, перейдя к математическим ожиданиям получаем
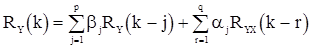 , (46)
, (46)
где 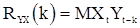 - взаимная корреляционная функция последовательностей X и Y. Так как
- взаимная корреляционная функция последовательностей X и Y. Так как 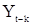 зависит только от членов входной последовательности X до момента
зависит только от членов входной последовательности X до момента 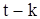 , то, очевидно, что
, то, очевидно, что 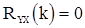 при
при 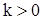 и
и 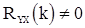 для
для 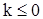 . Из (46) следует, что
. Из (46) следует, что
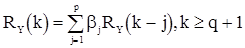 (47)
(47)
и для нормированной корреляционной функции
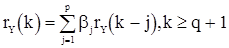 (47’)
(47’)
Это означает, что для с.п. АРСС(p,q) существует q значений корреляционной функции 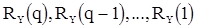 , которые связаны зависимостью (46) с q параметрами скользящего среднего
, которые связаны зависимостью (46) с q параметрами скользящего среднего 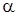 и p параметрами авторегрессии
и p параметрами авторегрессии 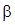 . Для решения разностных уравнений (47) и (47’) (для больших k) в качестве начальных необходимы p значений, например,
. Для решения разностных уравнений (47) и (47’) (для больших k) в качестве начальных необходимы p значений, например, 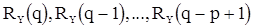 .
.
Дисперсию с.п. АРСС(p,q) 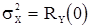 вместе с
вместе с 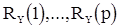 получим, решая систему уравнений, получающаяся из (46) при k=0,1,2,...,p.
получим, решая систему уравнений, получающаяся из (46) при k=0,1,2,...,p.
Спектральную плотность можно получить аналогично случаям «чистых» последовательностей АР(p) и СС(q).
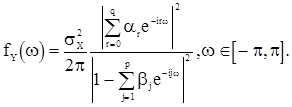 (48)
(48)
Рассмотрим подробнее случай АРСС(2,1):
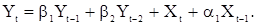 (49)
(49)
Из (46) имеем
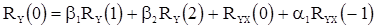 (50)
(50)
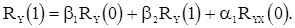 (51)
(51)
Чтобы найти 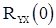 и
и 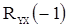 , умножим поочередно (49) на
, умножим поочередно (49) на 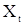 и
и 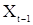 и перейдем к математическим ожиданиям. В результате получим
и перейдем к математическим ожиданиям. В результате получим
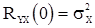 и
и 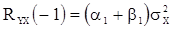 .
.
Тогда уравнениям (50) и (51) приобретают вид
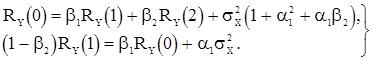 (52)
(52)
При 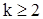
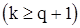 уравнения (47) в рассматриваемом случае имеют вид
уравнения (47) в рассматриваемом случае имеют вид
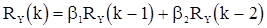 (53)
(53)
и вместе с уравнениями (52) позволяют определить последовательность 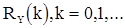 . В частности, из системы уравнений (52) и уравнения (53) при
. В частности, из системы уравнений (52) и уравнения (53) при 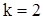 получаем формулу для дисперсии
получаем формулу для дисперсии
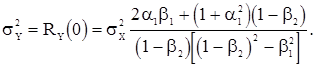 (54)
(54)
Спектральная плотность с.п. АРСС(2,1) согласно (48) имеет вид
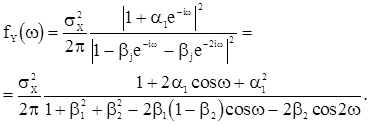 (55)
(55)
Наконец, рассмотрим часто употребляемую в различных прикладных науках с.п. АРСС(1,1). Она определяются разностным уравнением
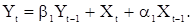 (56)
(56)
В этом случае входящая в с.п. авторегрессия имеет порядок p=1, и корень ее характеристического уравнения равен 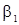 . Последова-тельность будет стационарной, если
. Последова-тельность будет стационарной, если 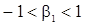 . Уравнения для корреляционной функции получаются из формул (46) и (47)
. Уравнения для корреляционной функции получаются из формул (46) и (47)
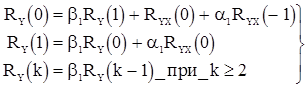 (57)
(57)
Выражения для 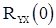 и
и 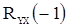 получаются аналогично предыдущему умножением (56) на
получаются аналогично предыдущему умножением (56) на 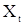 и
и 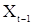 и переходом к математическим ожиданиям.
и переходом к математическим ожиданиям.
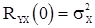 ,
,
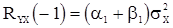 . (58)
. (58)
Из (57) и (58) получаем выражения корреляционной функции с.п. АРСС(1,1)
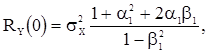
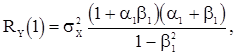 (59)
(59)
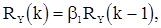
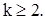
Из (59) следует, что при 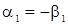 имеем
имеем 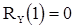 . Поэтому
. Поэтому 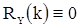 при всех значениях
при всех значениях 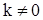 , т.е. последовательность
, т.е. последовательность 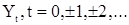 является некоррелированной.
является некоррелированной.
Спектральная плотность с.п. АРСС(1,1) будет иметь вид
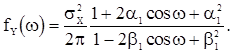 (60)
(60)
Дата: 2019-04-23, просмотров: 323.