Методом моментов

Одним из общих методов нахождения оценок параметров является метод моментов. Он заключается в приравнивании определенного количества выборочных моментов к соответствующим теоретическим параметрам, которые являются функциями от неизвестных параметров. Рассматривая количество моментов, равное числу оцениваемых параметров, получаем искомые оценки. На практике этод метод приводит к сравнительно простым вычислениям. Мы рассмотрим применение этого метода последовательно к оцениванию параметров последовательности АР(p), СС(q) и АРСС(p,q).

Для уравнений с.п.АР(p) метод моментов сводится к решению системы уравнений Юла-Уокера (11) для 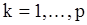 относительно параметров 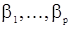. Вместо теоретических значений корреляционной функции  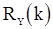следует подставить их оценки. В качестве таких оценок можно использовать 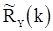,  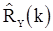и  и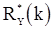з предыдущего раздела. Поскольку эти оценки состоятельны, то при больших T с вероятностью, близкой к единице, выборочная корреляционная матрица будет невырожденной и уравнения Юла-Уокера будут иметь решение 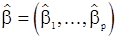, которое будет также состоятельной оценкой вектора 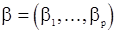. Однако оценки, найденные с помощью метода моментов, с точки зрения эффективности не являются наилучшими из возможных и даже при больших T они имеют наименьшую возможную дисперсию. В рассматриваемой модели с.п.АР(p) дисперсия «шума»  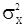тоже может являтся неизвестным параметром и для ее оценки может быть использованно равенство (14), в котором значения  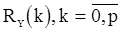следует заменить их оценками, как при оценивании 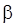, а сами параметры  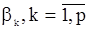в (14) должны быть заменены уже найденными оценками .

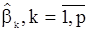Приведем два примера оценок, полученных по методу моментов.

1. Последовательность АР(1), определяемая уравнением (8), содержит один неизвестный параметр 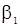. Уравнение Юла-Уокера имеет вид 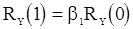. Подставляя в него вместо  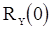и 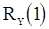 оценк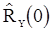и  и 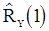 вида (77), получаем

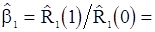
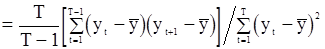.                   (87)

В нашем примере равенство (14) имеет вид

.
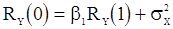Отсюда получается оценка дисперсии «шума»

.

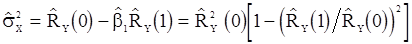2. Последовательность АР(2), определяемая уравнением (9), содержит неизвестные параметр 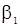 и 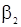. Система уравнений Юла-Уокера имеет вид

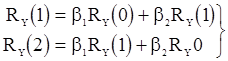
и дает оценки

.
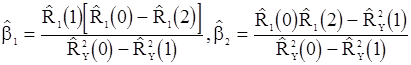Оценка для дисперсии «шума» 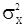 будет иметь вид

,
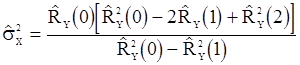В случае последовательности СС(q) метод моментов приводит к системе нелинейных уравнений относительно параметров 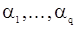, если в (33) полагать 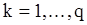. Два метода решения такой нелинейной системы изложены в [3, с.226-229]. Приведем здесь один из них. Это так называемый линейно сходящийся итеративный процесс.

Из выражений (34) и (33) для корреляционной функции процесса СС(q) можно найти оценки параметров 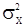,  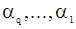точно в том порядке, как здесь указано, при помощи итераций

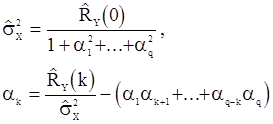                              (88)
с условием, что 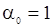. Параметры  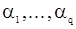приравниваются к нулю в самом начале итеративной процедуры; значения  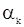и 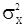, используемые в любом цикле вычисления - это последние из доступных оценок этих величин. Например, в случае  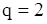уравнения (88) имеют вид

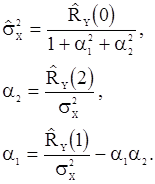
В случае  уравнения (88) приобретают вид

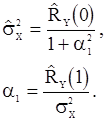
После исключения из этих уравнений величины 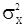 приходим к квадратному уравнению относительно  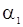и находим оценку

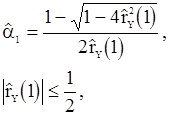                                                   (89)
в которой 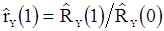. Затем получаем оценку

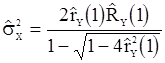.                                                   (90)

Наконец, рассмотрим оценку параметров в смешанной модели АРСС(p,q). Для оценки параметров авторегрессии 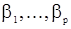 можно использовать p-уравнения вида (47) для 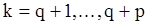, в которых значения корреляционной функции  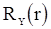заменяются выборочными значениями (оценками). Затем введем вспомогательный процесс W, полагая

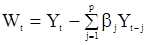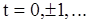,                               (91)
Тогда уравнению (43) можно придать вид

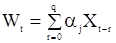
и, следовательно, с.п.W можно рассматривать как «чистую» последовательность CC(q). Исходя из равенства (91), можно выразить корреляционную функцию последовательности W через значения корреляционной функции последовательности Y. Можно показать, что

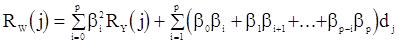,    (92)

где ; , .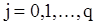       
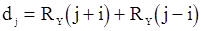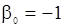Далее, пользуясь уже найдеными оценками для 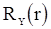 и параметров 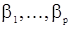, по формулам (92) будем иметь оценки для корреляционной функции 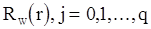. На заключительном этапе используем описанный выше линейно сходящийся итеративный процесс для оценки неизвестных 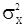,  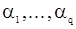либо (в частном случае 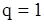) воспользуемся готовыми формулами (89) и (90), в которых оценк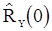и  и 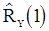 должны быть заменены оценкам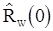и  и .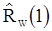

Оценивание параметров