1. Выяснить, является ли функция ограниченно-детерминированной и найти ее вес.
1) 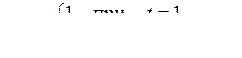
2) 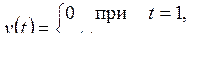
3) 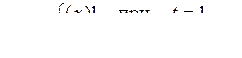
4) 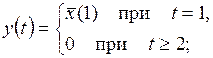
5) 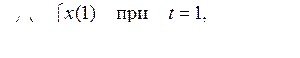
6) 
7) 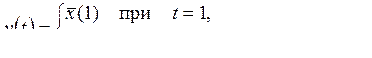
8) 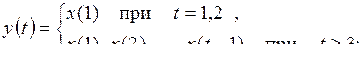
9) 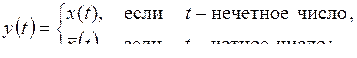
10) 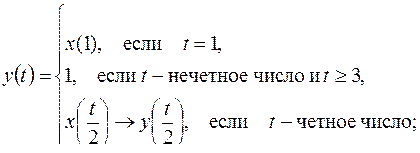
11) 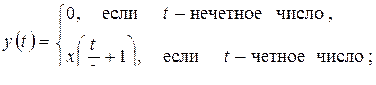
12) 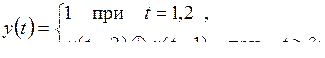
13) 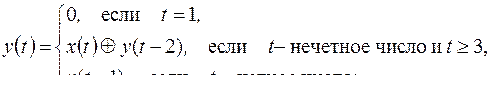
14) 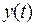 есть t-я цифра после запятой в двоичном разложении числа
есть t-я цифра после запятой в двоичном разложении числа  ;
;
15) 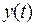 есть t-я цифра после запятой в двоичном разложении числа
есть t-я цифра после запятой в двоичном разложении числа 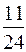 .
.
2. Построить диаграмму Мура, каноническую таблицу и канонические уравнения для функции 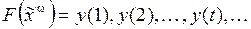 .
.
1) 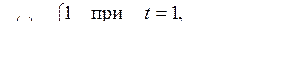
2) 
3) 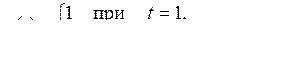
4) 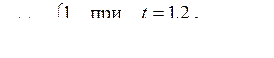
5) 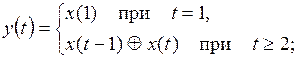
6) 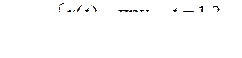
7) 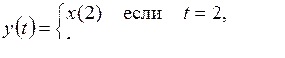
8) 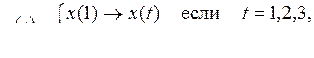
9) 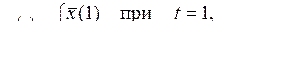
10) 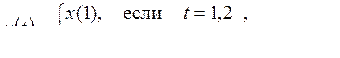
11) 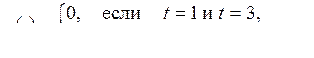
12) 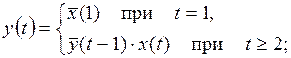
13) 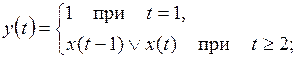
14) 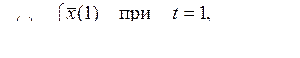
15) 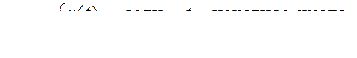
16) 
17) 
18) 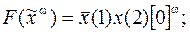
19) 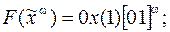
20) 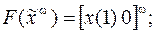
21) 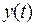 есть
есть 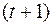 -я цифра после запятой в двоичном разложении числа
-я цифра после запятой в двоичном разложении числа 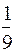 ;
;
22) 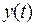 есть
есть 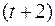 -я цифра после запятой в двоичном разложении числа
-я цифра после запятой в двоичном разложении числа 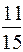 ;
;
23) 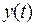 есть
есть 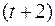 -я цифра после запятой в двоичном разложении числа
-я цифра после запятой в двоичном разложении числа 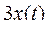 ;
;
24) 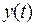 есть t-я цифра после запятой в двоичном разложении числа
есть t-я цифра после запятой в двоичном разложении числа 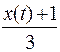 ;
;
25) 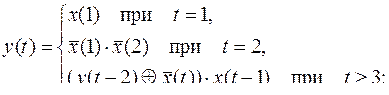
26) 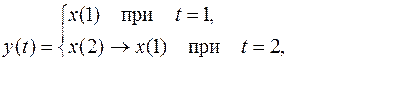
27) 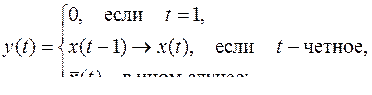
28) 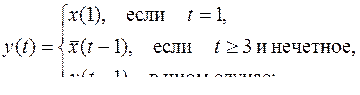
29) 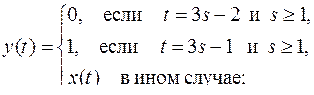
30) 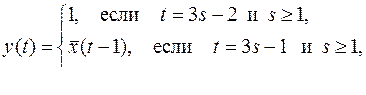
31) 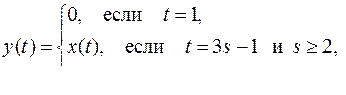
32) 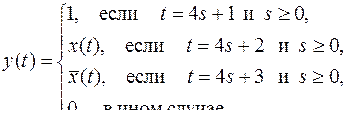
3. Для каждой из диаграмм (рис. 7.29) построить приведенную диаграмму Мура.
| 1) | 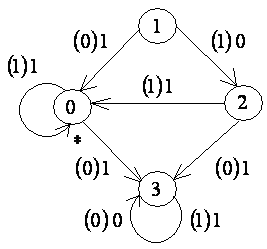
|
| 2) | 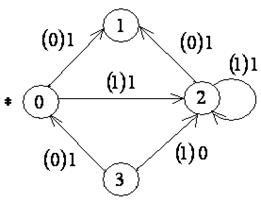
|
| 3) |
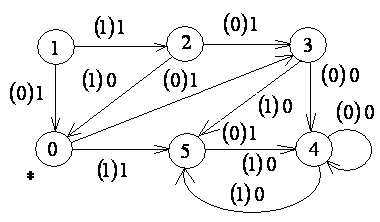 Рис. 7.29
Рис. 7.29
|
4. Найти вес ограниченно-детерминированной функции 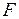 из
из 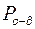 , заданной каноническими уравнениями:
, заданной каноническими уравнениями:
1) 
2) 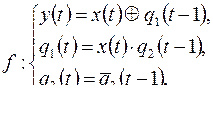
3) 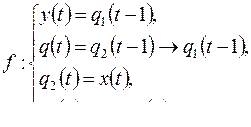
4) 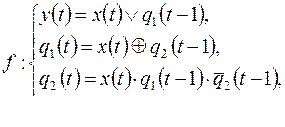
5) 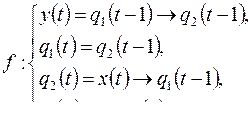
6) 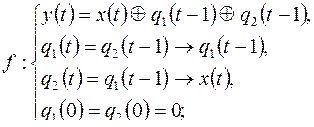
7) 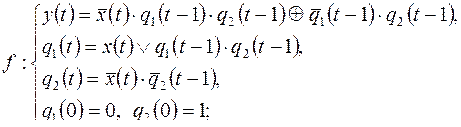
8) 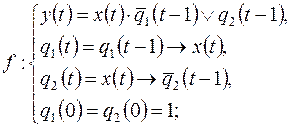
9) 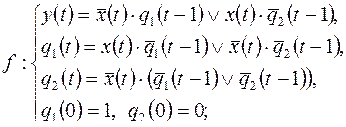
10) 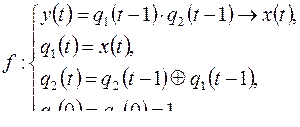
5. Для суперпозиции 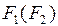 ограниченно-детерминированной функций
ограниченно-детерминированной функций 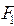 и
и 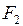 из
из 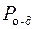 построить канонические уравнения и приведенную диаграмму Мура.
построить канонические уравнения и приведенную диаграмму Мура.
1) 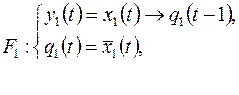
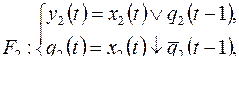
2) 

3) 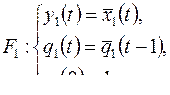
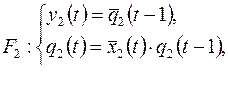
4) 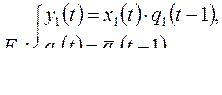
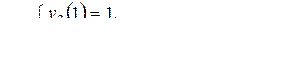
5) 
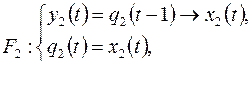
6) функция 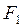 задается диаграммой Мура, изображенной на рис. 7.30.
задается диаграммой Мура, изображенной на рис. 7.30.
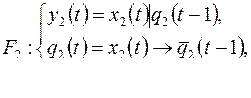
| 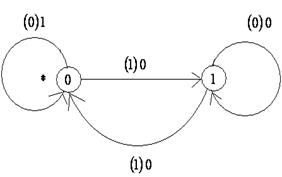 Рис. 7.30
Рис. 7.30
|
7) 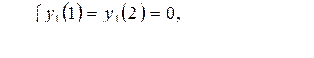
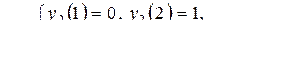
6. Построить канонические уравнения и приведенную диаграмму Мура ограниченно-детерминированной функции, получающейся из функции 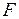 введением обратной связи по переменным
введением обратной связи по переменным 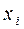 ,
, 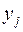 .
.
1) 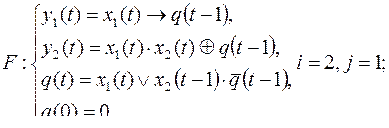
2) 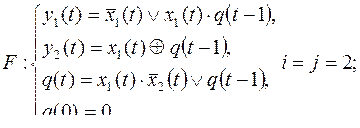
3) 
4) 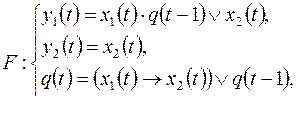
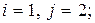
5) 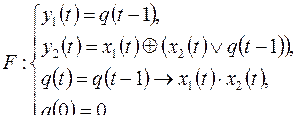
а) 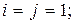 б)
б) 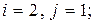
6) 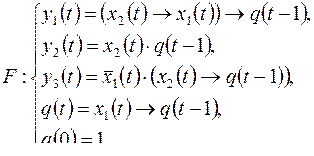
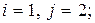
7) 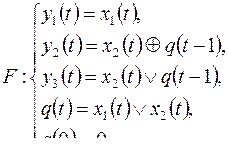
а) 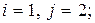 б)
б) 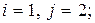 в)
в) 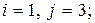
8) 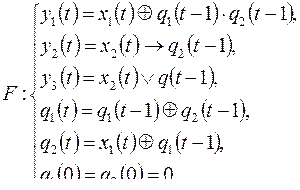
а) 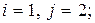 б)
б) 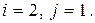
7. Найти вес ограниченно-детерминированной функции, получающейся из ограниченно-детерминированной функции 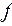 введением обратной связи по переменным
введением обратной связи по переменным 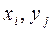 .
.
1) 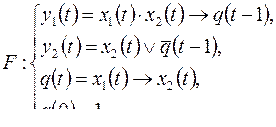
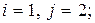
2) 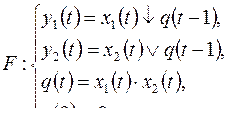
а) 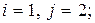 б)
б) 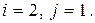
3) 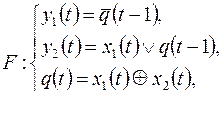
а) 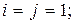 б)
б) 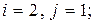 в)
в) 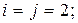
4) 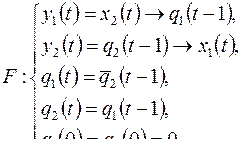
а) 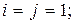 б)
б) 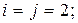
5) 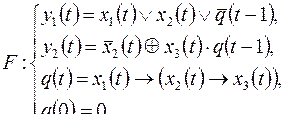
а) 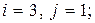 б)
б) 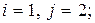
6) 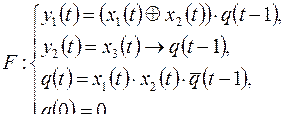
а) 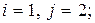 б)
б) 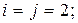 в)
в) 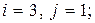
7) 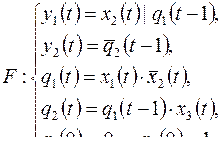
а) 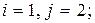 б)
б) 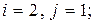 в)
в) 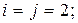
г) 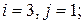 д)
д) 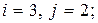
8. Найти вес ограниченно-детерминированной функции, получающейся из ограниченно-детерминированной функции 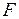 с помощью операции отождествления входных переменных
с помощью операции отождествления входных переменных 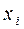 и
и 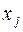 .
.
1) 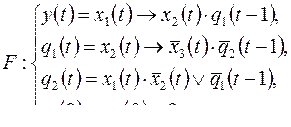
а) 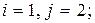 б)
б) 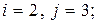
2) 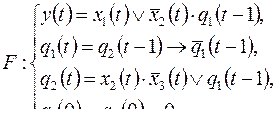
а) 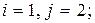 б)
б) 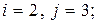
3) 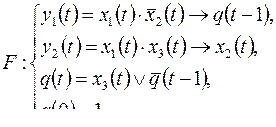
а) 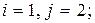 б)
б) 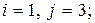 в)
в) 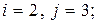
4) 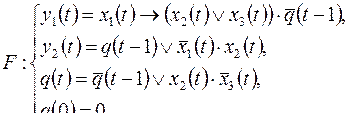
а) 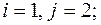 б)
б) 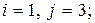 в)
в) 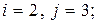
9. Найти вес суперпозиции 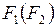 , если:
, если:
1) 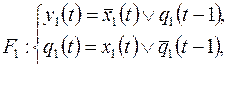
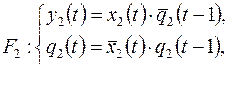
2) 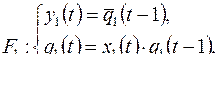
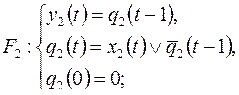
3) 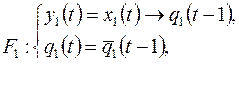
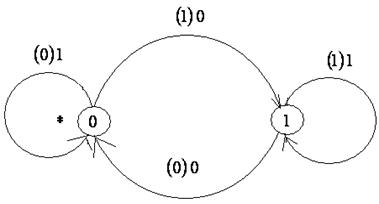 Рис. 7.31
Рис. 7.31
|
Функция 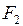 задается диаграммой Мура, изображенной на рис. 7.31.
задается диаграммой Мура, изображенной на рис. 7.31.
10. Для функции 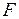 из
из 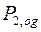 построить схему над множеством, состоящим из элемента единичной задержки и функций, порожденных дизъюнкцией, конъюнкцией и отрицанием:
построить схему над множеством, состоящим из элемента единичной задержки и функций, порожденных дизъюнкцией, конъюнкцией и отрицанием:
1) 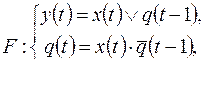
2) 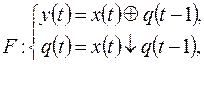
3) функция 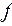 задается канонической табл. 7.6 и
задается канонической табл. 7.6 и 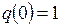 ;
;
Таблица 7.6
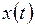
| 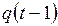
| 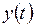
| 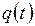
|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
4) функция 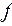 задается канонической табл. 7.7 и
задается канонической табл. 7.7 и  ;
;
Таблица 7.7
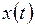
| 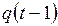
| 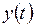
| 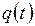
|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 |
5) 
6) 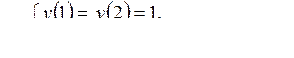
7) 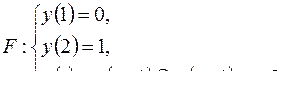
8) 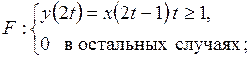
9) 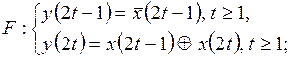
10) 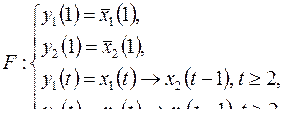
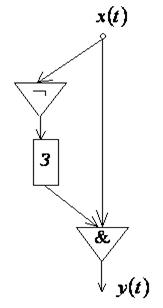
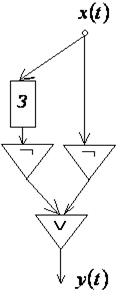
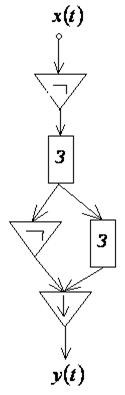
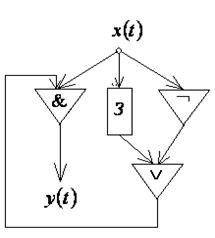
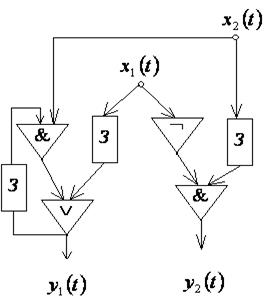
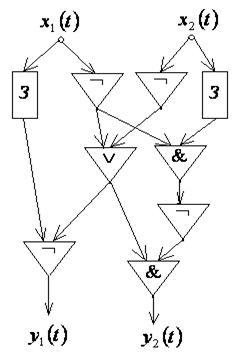
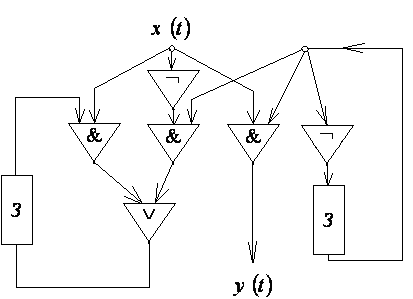
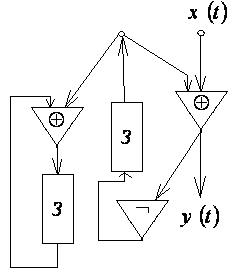
11. По схемам, приведенным на рис. 7.32, 7.33, 7.34, построить канонические уравнения автоматной функции.
| 
| 
| 
|
Рис. 7.32
| 
|
Рис. 7.33
| 
|
Рис. 7.34
Ответы к главе 7
1. 1), 2), 4), 5), 9), 10) ограниченно-детерминированной (о.-д.) функция веса 2. 3), 7), 8) о.-д. функция веса 3. 6) 14) о.-д. функция веса 4. 11) Функция не является о.-д. 12), 15) о.-д. функция веса 5. 13) о.-д. функция веса 7.
2. 1) 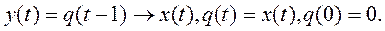
2) 

4) 
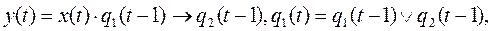
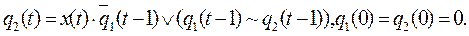
16). 19, 23), 29) Вес функции равен 3. 17), 25) Вес функции равен 6. 20) Вес функции равен 4. 26), 28), 30) Вес функции равен 5.
4. 1) Вес функции равен 1. 2), 5) Вес функции равен 4. 3), 7), 8) Вес функции равен 2. 4), 6), 9), 10) Вес функции равен 3.
5. 1) 
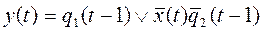 ,
,
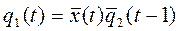 ,
,
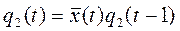 ,
,
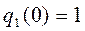 ,
, 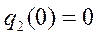 .
.
Вес суперпозиции f1(f2) равен 2, она может быть задана следующим каноническими уравнениями и начальными условиями:
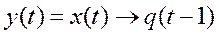 ,
, 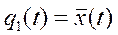 ,
, 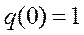 .
.
2) Вес суперпозиции равен 3,
3) Вес суперпозиции равен 1.
5) Вес суперпозиции равен 2.
6) Вес суперпозиции равен 4,
7) Вес суперпозиции равен 5.
6. 1) Получается о.-д. функция веса 2. 2) Получается о.-д. функция веса, порожденная отрицанием. 7) а)-в) Получается о.-д. функция веса 2. 8) а) Получается о.-д. функция веса 3. б) Получается о.-д. функция веса 4.
7. 1) Вес равен 1. 2) а) Вес равен 2. б) Вес равен 1. 3) а),в) Вес равен 1. б) Вес равен 2. 4) а),б) Вес равен 4. 5) а) Вес равен 2. б) Вес равен 1. 6) а), в) Вес равен 1. б) Вес равен 2. 7) а) Вес равен 4. б), д) Вес равен 2. в), г) Вес равен 3.
8. 1) а) Вес равен 4. б) Вес равен 2. 2) а), б) Вес равен 3. 3) а) Вес равен 1. б), в) Вес равен 2. 4) а)-в) Вес равен 2.
9. 1), 4) Вес равен 1. 2) Вес равен 2. 3) Вес равен 3. 5) Вес равен 7.
ГЛАВА 8. ТИПОВЫЕ ЗАДАНИЯ
1. Доказать тождества, используя только определения операций над множествами.
2. C помощью алгебры логики проверить истинность соотношения для любых множеств A, B, C. Если соотношение неверно, построить контрпример.
3. Найти область определения, область значений отношения 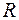 . Является ли отношение
. Является ли отношение 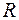 рефлексивным, симметричным, антисимметричным, транзитивным?
рефлексивным, симметричным, антисимметричным, транзитивным?
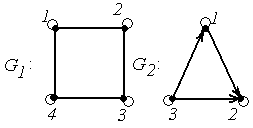
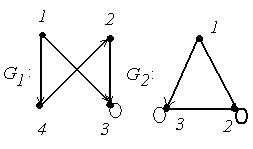
4. Для графов 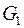 и
и 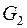 найти матрицы смежности вершин и инцидентности.
найти матрицы смежности вершин и инцидентности.
5. Проверить эквивалентность формул двумя способами:
а) составлением таблиц истинности,
б) эквивалентными преобразованиями.
6. C помощью эквивалентных преобразований построить для заданной функции ДНФ, КНФ, CДНФ, CКНФ, полином Жегалкина.
7. Найти сокращенную, все тупиковые и минимальные ДНФ булевой функции 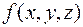 двумя способами:
двумя способами:
а) методом Квайна,
б) с помощью карт Карно.
К каким классам Поста принадлежит функция?
8. Выяснить, полна ли в 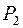 система функций
система функций 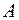 . Если полна, то выделить все возможные базисы.
. Если полна, то выделить все возможные базисы.
9. Построить информативное дерево, усеченное дерево, найти вес функции, построить диаграмму Мура, каноническую таблицу, канонические уравнения автоматной функции после доопределения и минимизации методом Карно для функции 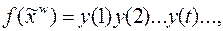 где
где 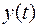 есть t-я цифра после запятой в двоичном разложении заданной дроби.
есть t-я цифра после запятой в двоичном разложении заданной дроби.
10. Для суперпозиции 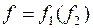 построить информативное дерево, найти вес полученной функции, написать канонические уравнения.
построить информативное дерево, найти вес полученной функции, написать канонические уравнения.
Вариант 1
1. 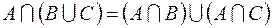 ,
,
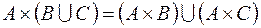 .
.
2. 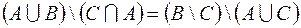 .
.
3. 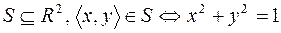 .
.
4.
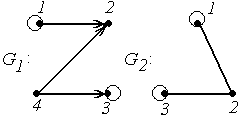
|
5. 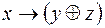 и
и 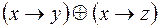 .
.
6. 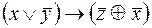 .
.
7. 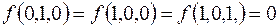
(на остальных наборах  ).
).
8. 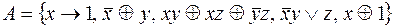 .
.
9. 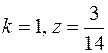 .
.
10. 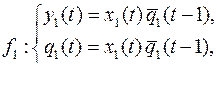
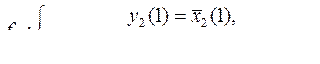
Вариант 2
1. 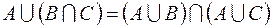 ,
,
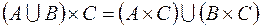 .
.
2. 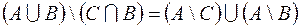 .
.
3. 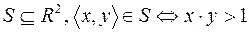 .
.
4.
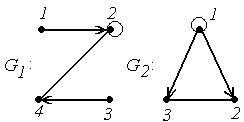
|
5. 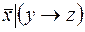 и
и 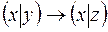 .
.
6. 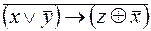 .
.
7. 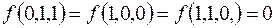
(на остальных наборах  ).
).
8. 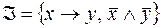 .
.
9. 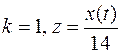 .
.
10. 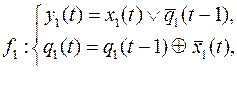
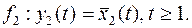
Вариант 3
1. 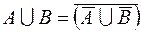 ,
,
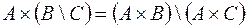 .
.
2. 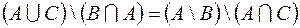 .
.
3. 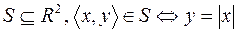 .
.
4.
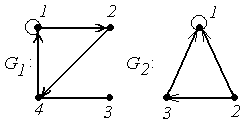
|
5. 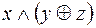 и
и 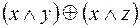 .
.
6. 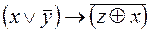 .
.
7. 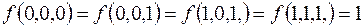
(на остальных наборах  ).
).
8. 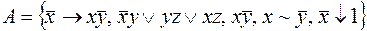 .
.
9. 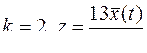 .
.
10. 
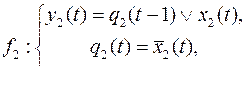
Вариант 4
1. 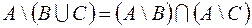 ,
,
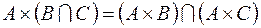 .
.
2. 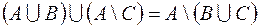 .
.
3. 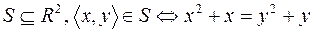 .
.
4.
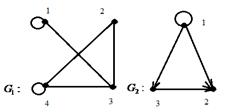
|
5. 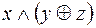 и
и 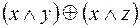 .
.
6. . 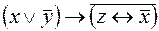 .
.
7. 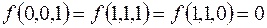
(на остальных наборах  ).
).
8. 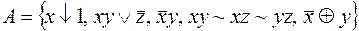 .
.
9. 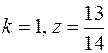 .
.
10. 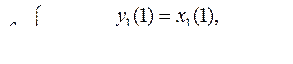
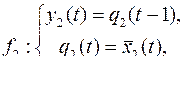
Вариант 5
1. 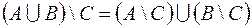 ,
,
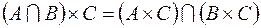 .
.
2. 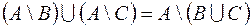 .
.
3. 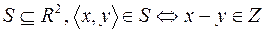 .
.
4.
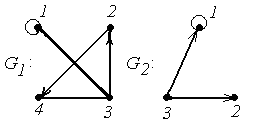
|
5. 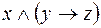 и
и 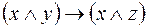 .
.
6. 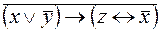 .
.
7. 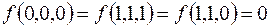
(на остальных наборах  ).
).
8. 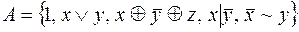 .
.
9. 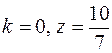 .
.
10. 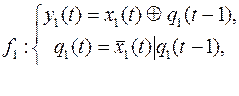
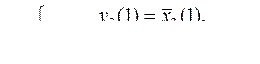
Вариант 6
1. 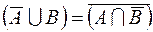 ,
,
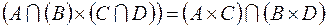 .
.
2. 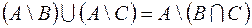 .
.
3. 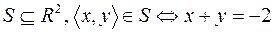 .
.
4.
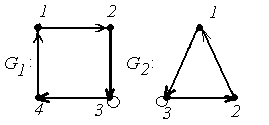
|
5. 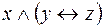 и
и 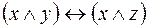 .
.
6. 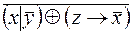 .
.
7. 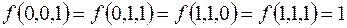
(на остальных наборах  ).
).
8. 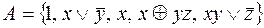 .
.
9. 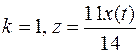 .
.
10. 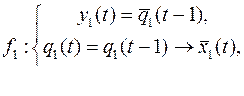
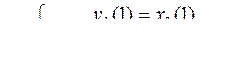
Вариант 7
1. 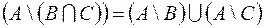 ,
,
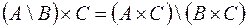 .
.
2. 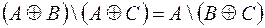 .
.
3. 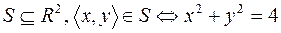 .
.
4.

|
5. 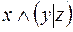 и
и 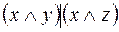 .
.
6. 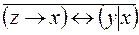 .
.
7. 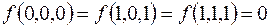
(на остальных наборах  ).
).
8. 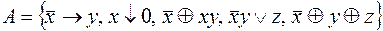 .
.
9. 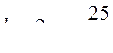 .
.
10. 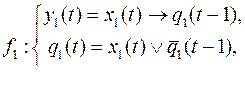
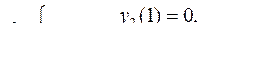
Вариант 8
1. 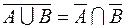 ,
,
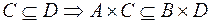 .
.
2. 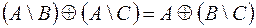 .
.
3.  .
.
4.
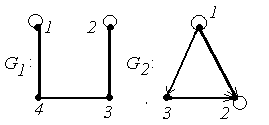
|
5. 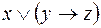 и
и 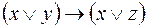 .
.
6. 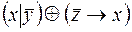 .
.
7. 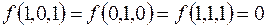
(на остальных наборах  ).
).
8. 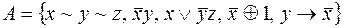 .
.
9. 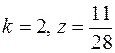 .
.
10. 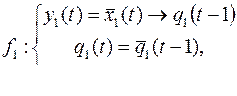
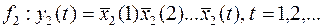 .
.
Вариант 9
1. 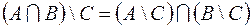 ,
,
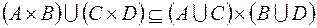 .
.
2. 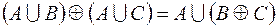 .
.
3. 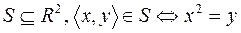 .
.
4.

|
5. 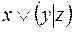 и
и 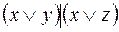 .
.
6. 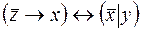 .
.
7. 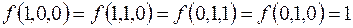
(на остальных наборах  ).
).
8. 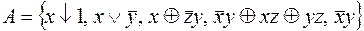 .
.
9. 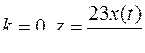 .
.
10. 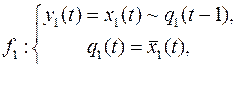
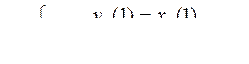
Вариант 10
1. 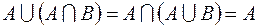 ,
,
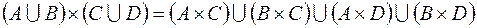 .
.
2. 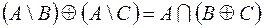 .
.
3.  .
.
4.
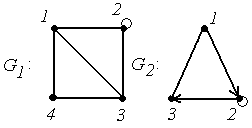
|
5. 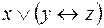 и
и 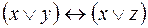 .
.
6. 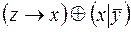 .
.
7. 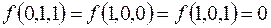
(на остальных наборах  ).
).
8. 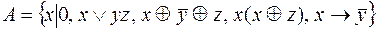 .
.
9. 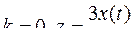 .
.
10. 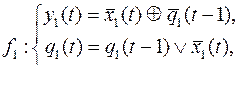
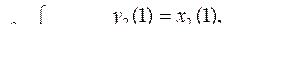
Вариант 11
1. 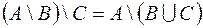 ,
,
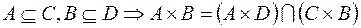 .
.
2. 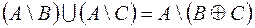 .
.
3. 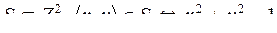 .
.
4.
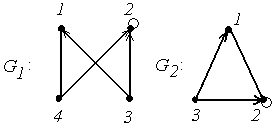
|
5. 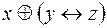 и
и 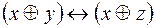 .
.
6.  .
.
7. 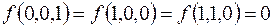
(на остальных наборах  ).
).
8. 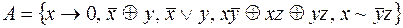 .
.
9. 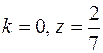 .
.
10. 
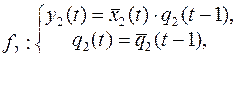
Вариант 12
1. 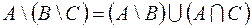 ,
,
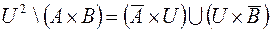 .
.
2. 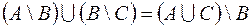 .
.
3. 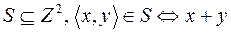 кратно 3.
кратно 3.
4.
|
5. 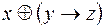 и
и 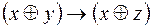 .
.
6. 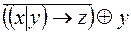 .
.
7. 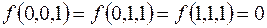
(на остальных наборах  ).
).
8. 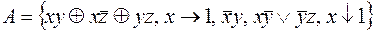 .
.
9. 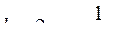 .
.
10. 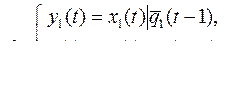

Вариант 13
1. 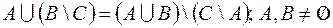 ,
,
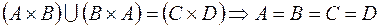 .
.
2. 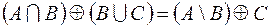 .
.
3. 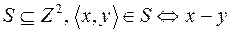 кратно 2.
кратно 2.
4.
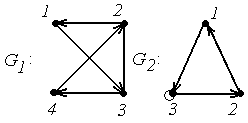
|
5. 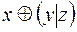 и
и 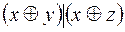 .
.
6. 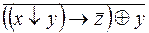 .
.
7. 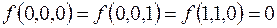
(на остальных наборах  ).
).
8. 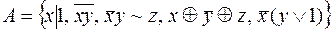 .
.
9. 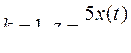 .
.
10. 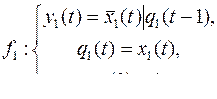
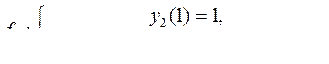
Вариант 14
1. 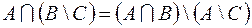 ,
,
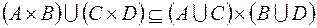 .
.
2. 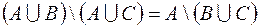 .
.
3. 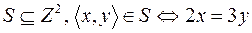 .
.
4.
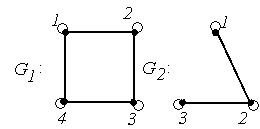
|
5. 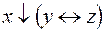 и
и 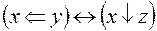 .
.
6. 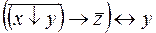 .
.
7. 
(на остальных наборах  ).
).
8. 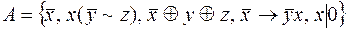 .
.
9. 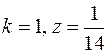 .
.
10. 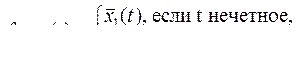
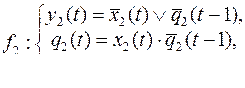
Вариант 15
1. 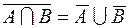 ,
,
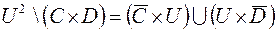 .
.
2. 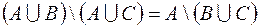 .
.
3. 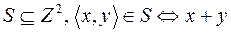 нечетно.
нечетно.
4.
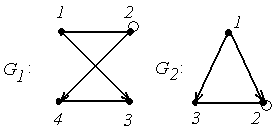
|
5. 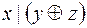 и
и 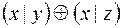 .
.
6. 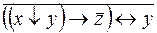 .
.
7. 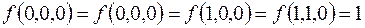
(на остальных наборах  ).
).
8. 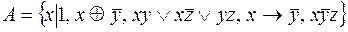 .
.
9.  .
.
10. 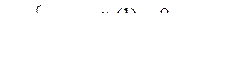
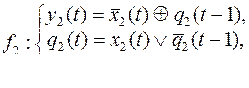
Вариант 16
1. 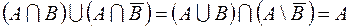 ,
,
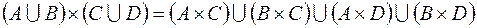 .
.
2. 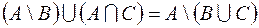 .
.
3. 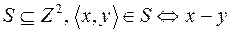 четно.
четно.
4.
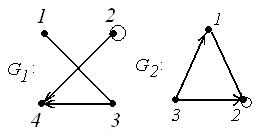
|
5. 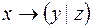 и
и 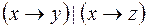 .
.
6. 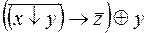 .
.
7. 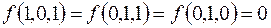
(на остальных наборах  ).
).
8. 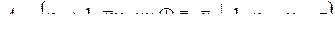 .
.
9. 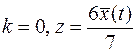 .
.
10. 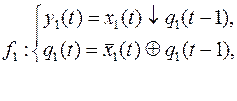
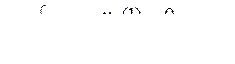
Вариант 17
1. 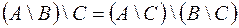 ,
,
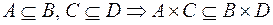 .
.
2. 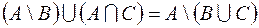 .
.
3.  .
.
4.
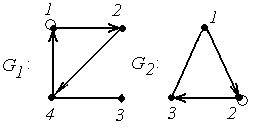
|
5. 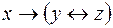 и
и 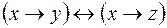 .
.
6. 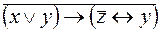 .
.
7. 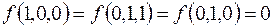
(на остальных наборах  ).
).
8. 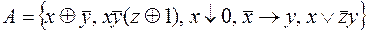 .
.
9. 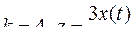 .
.
10. 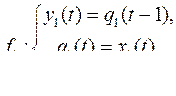
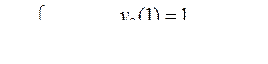
Вариант 18
1. 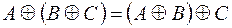 ,
,
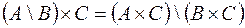 .
.
2. 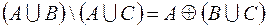 .
.
3. 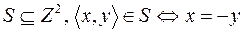 .
.
4.
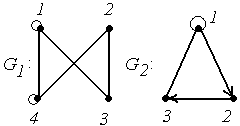
|
5. 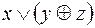 и
и 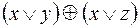 .
.
6. 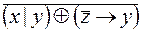 .
.
7. 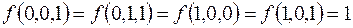
(на остальных наборах  ).
).
8. 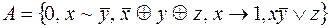 .
.
9. 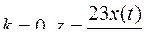 .
.
10. 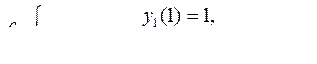
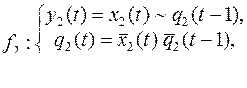
Вариант 19
1. 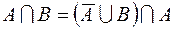 ,
,
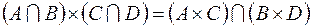 .
.
2. 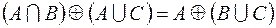 .
.
3. 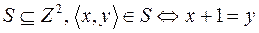 .
.
4.
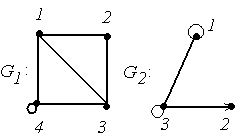
|
5. 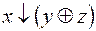 и
и 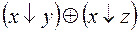 .
.
6. 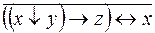 .
.
7. 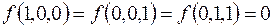
(на остальных наборах  ).
).
8. 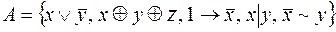 .
.
9. 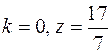 .
.
10. 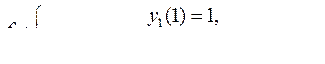
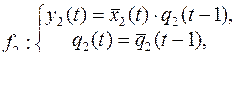
Вариант 20
1. 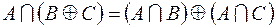 ,
,
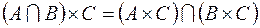 .
.
2. 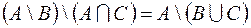 .
.
3. 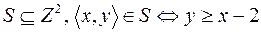 .
.
4.
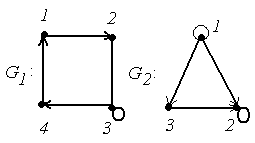
|
5. 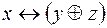 и
и 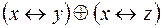 .
.
6. 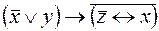 .
.
7. 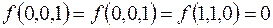
(на остальных наборах  ).
).
8. 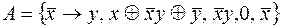 .
.
9. 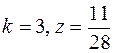 .
.
10. 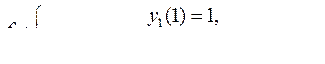
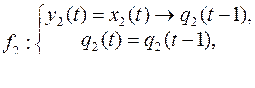
Вариант 21
1. 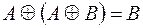 ,
,
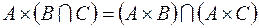 .
.
2. 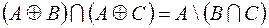 .
.
3. 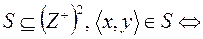 НОД
НОД 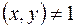 , где
, где 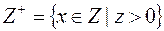 .
.
4.
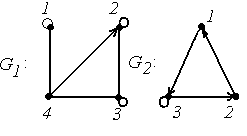
|
5. 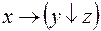 и
и 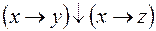 .
.
6. 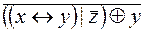 .
.
7. 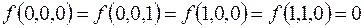
(на остальных наборах  ).
).
8. 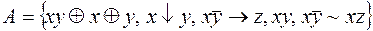 .
.
9. 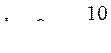 .
.
10. 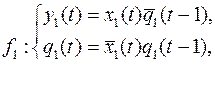

Вариант 22
1. 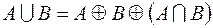 ,
,
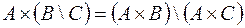 .
.
2. 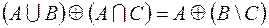 .
.
3.  .
.
4.
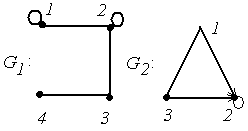
|
5. 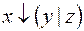 и
и 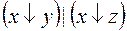 .
.
6. 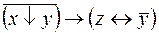 .
.
7. 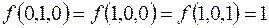
(на остальных наборах  ).
).
8. 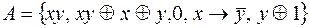 .
.
9. 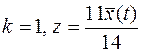 .
.
10. 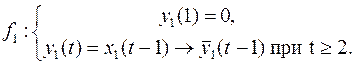
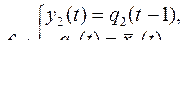
Вариант 23
1. 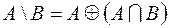 ,
,
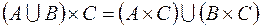 .
.
2. 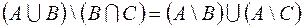 .
.
3. 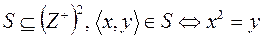 , где
, где 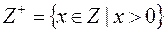 .
.
4.
|
5. 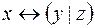 и
и 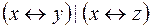 .
.
6. 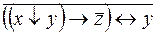 .
.
7. 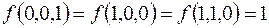
(на остальных наборах  ).
).
8.  .
.
9. 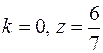 .
.
10. 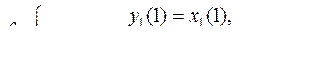
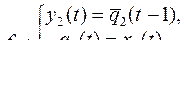
Вариант 24
1. 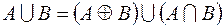 ,
,
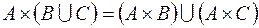 .
.
2. 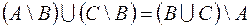 .
.
3. 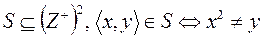 , где
, где 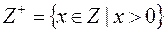 .
.
4.
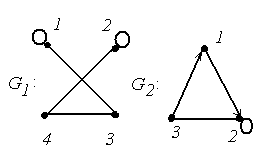
|
5. 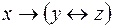 и
и 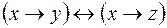 .
.
6.  .
.
7. 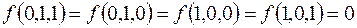
(на остальных наборах  ).
).
8. 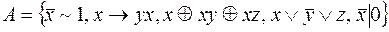 .
.
9. 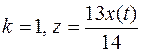 .
.
10. 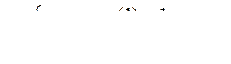
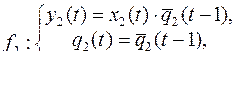
Вариант 25
1. 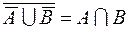 ,
,
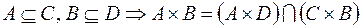 .
.
2. 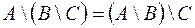 .
.
3. 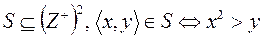 , где
, где 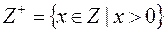 .
.
4.
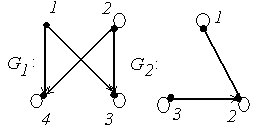
|
5. 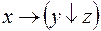 и
и 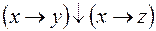 .
.
6. 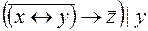 .
.
7. 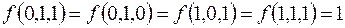
(на остальных наборах  ).
).
8. 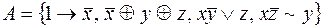 .
.
9.  .
.
10. 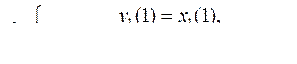
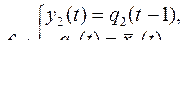
ГЛАВА 9. РЕШЕНИЕ ТИПОВОГО ЗАДАНИЯ
Задание 1. Доказать тождества, используя только определения операций над множествами.
1.1. 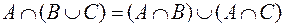 .
.
Решение. Пусть 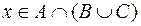 , тогда
, тогда 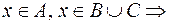
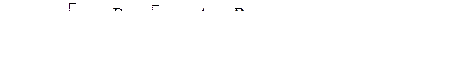 Пусть
Пусть 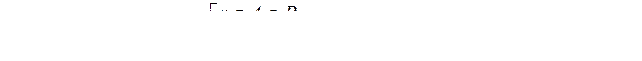 Замечание. Обозначение
Замечание. Обозначение 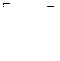 означает «совокупность», т. е.
означает «совокупность», т. е.  или
или 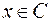 , что означает
, что означает  .
.
1.2. 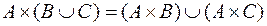 .
.
Решение. Пусть 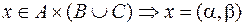 , где
, где 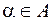
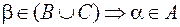 и
и 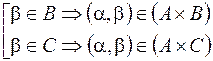
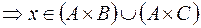 .
.
Пусть 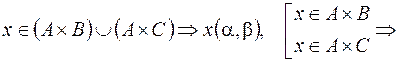
 .
.
Задание 2. C помощью алгебры логики проверьте истинность соотношения 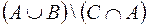 =
= 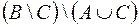 для любых множеств А, В, С.
для любых множеств А, В, С.
Решение.
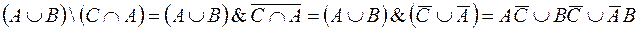
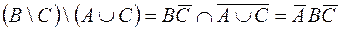
Cоотношение неверно, множество 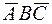 является подмножеством
является подмножеством 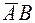 и, следовательно,
и, следовательно, 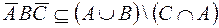 .
.
Задание 3. Найти область определения, область значений отношения S: 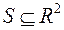 ,
, 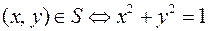 . Является ли отношение S рефлексивным, симметричным, антисимметричным, транзитивным.
. Является ли отношение S рефлексивным, симметричным, антисимметричным, транзитивным.
Решение. Область определения 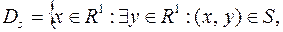 т. е.
т. е. 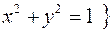 . Здесь
. Здесь 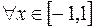 существует
существует 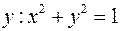 , следовательно DS=[–1,1]. Область значений
, следовательно DS=[–1,1]. Область значений 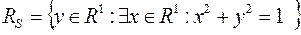 ,
, 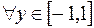 существует x:
существует x: 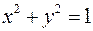 , следовательно RS = [–1,1].
, следовательно RS = [–1,1].
Отношение S называется рефлексивным, если 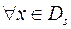 пара
пара 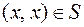 , т. е.
, т. е. 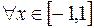 должно выполняться
должно выполняться 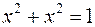 , что неверно, следовательно отношение не является рефлексивным.
, что неверно, следовательно отношение не является рефлексивным.
Отношение S называется симметричным, если 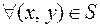 пара
пара 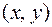 также будет принадлежать S. В данном примере если
также будет принадлежать S. В данном примере если 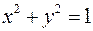 , то
, то 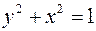 , следовательно отношение S симметрично.
, следовательно отношение S симметрично.
Отношение S называется транзитивным, если 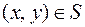 и
и 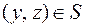 , то пара
, то пара  . В данном примере если
. В данном примере если 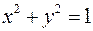 и
и 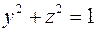 , то
, то 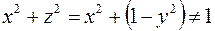 , например:
, например: 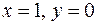 удовлетворяет условию
удовлетворяет условию 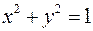 , пара
, пара 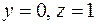 также удовлетворяет условию
также удовлетворяет условию 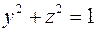 , но пара
, но пара 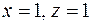 не удовлетворяет условию
не удовлетворяет условию 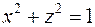 . Отношение S не является транзитивным.
. Отношение S не является транзитивным.
Задание 4. Для графа G найдите матрицы смежности и инцидентности.
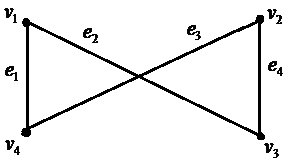
Матрица смежности вершин
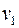
| 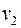
| 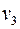
| 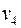
| |
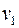
| 0 | 0 | 1 | 1 |
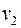
| 0 | 0 | 1 | 1 |
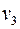
| 1 | 1 | 0 | 0 |
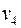
| 1 | 1 | 0 | 0 |
Матрица инцидентности
| e1 | e2 | e3 | e4 | |
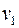
| 1 | 1 | 0 | 0 |
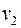
| 0 | 0 | 1 | 1 |
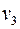
| 0 | 1 | 0 | 1 |
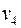
| 1 | 0 | 1 | 0 |
Задание 5. Проверить эквивалентность формул двумя способами: с помощью таблиц истинности и с помощью эквивалентных преобразований: 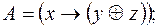
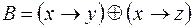 .
.
Решение. Построим таблицы истинности для формул 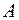 и
и  .
.
| x y z | 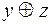
| A | 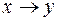
| 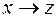
| B |
| 0 0 0 | 0 | 1 | 1 | 1 | 0 |
| 0 0 1 | 1 | 1 | 1 | 1 | 0 |
| 0 1 0 | 1 | 1 | 1 | 1 | 0 |
| 0 1 1 | 0 | 1 | 1 | 1 | 0 |
| 1 0 0 | 0 | 0 | 0 | 0 | 0 |
| 1 0 1 | 1 | 1 | 0 | 1 | 1 |
| 1 1 0 | 1 | 1 | 1 | 0 | 1 |
| 1 1 1 | 0 | 0 | 1 | 1 | 0 |
Формулы А и В не эквивалентны.
Преобразуем формулы 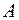 и
и  .
.
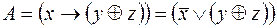 ,
,
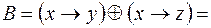
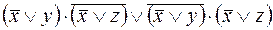 =
=
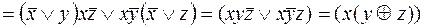 , очевидно, что формулы
, очевидно, что формулы 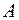 и
и  не эквивалентны.
не эквивалентны.
Задание 6. C помощью эквивалентных преобразований построить ДНФ, СДНФ, КНФ, CКНФ, полином Жегалкина для функции 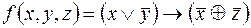 .
.
Решение. 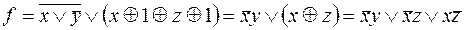 , полученное представление является ДНФ.
, полученное представление является ДНФ.
Получим СДНФ 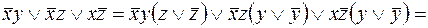
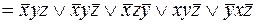 .
.
Получим КНФ
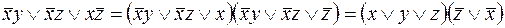 .
.
Получим СКНФ
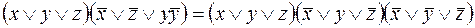 .
.
Построим полином Жегалкина
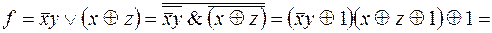
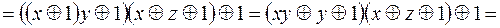
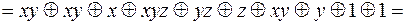
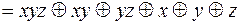 .
.
Задание 7. Найдите сокращенную, все тупиковые и минимальные ДНФ булевой функции f(x, y, z) двумя способами:
а) методом Квайна,
б) с помощью карт Карно.
Решение. Для функции f(010) = f(011) = f(100) = f(110) = 0. (На остальных наборах f(x, y, z) = 1.)
Построим таблицу истинности.
| x | y | z | f(x, y, z) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Найдем для нее СДНФ, из которой поместим в матрицу Квайна конституенты единицы:
 .
.
Теперь найдем СКНФ:
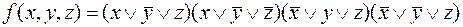 .
.
Теперь произведя операции склеивания, а затем поглощения, из СКНФ получим 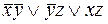 . Полученные простые импликанты (ПИ) также поместим в матрицу Квайна.
. Полученные простые импликанты (ПИ) также поместим в матрицу Квайна.
| ПИ | Конституенты единицы | ||||
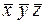
| 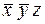
| 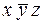
| 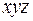
| ||
| 1 | 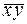
| + | + | ||
| 2 | 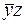
| + | + | ||
| 3 | 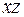
| + | + | ||
Найдем решеточные выражения:
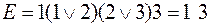
Следовательно, тупиковая ДНФ имеет вид: 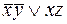 . Она и будет минимальной ДНФ.
. Она и будет минимальной ДНФ.
Найдем сокращению ДНФ методом карт Карно.
| y | 0 | 0 | 1 | 1 |
| z | 0 | 1 | 1 | 0 |
| x | ||||
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
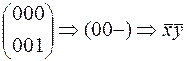 (ПИ)
(ПИ)
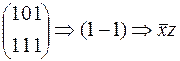 (ПИ)
(ПИ)
Карта Карно дает сокращенную ДНФ: 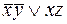 , которая совпала с ТДНФ и МДНФ.
, которая совпала с ТДНФ и МДНФ.
Задание 8. Выяснить, полна ли в 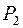 система функций
система функций 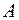 . Если полна, то выделить всевозможные базисы.
. Если полна, то выделить всевозможные базисы.
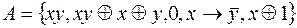 .
.
Решение.
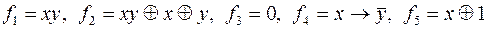 .
.
Критериальная таблица
| T 0 | T 1 | L | S | M | |
| f1 | + | + | – | – | + |
| f2 | + | + | – | – | + |
| f3 | + | – | + | – | + |
| f4 | – | – | – | – | – |
| f5 | – | – | + | + | – |
T0 – класс функций, сохраняющих константу 0.
T1 – класс функций, сохраняющих константу 1.
L – класс линейных функций.
S – класс самодвойственных функций.
M – класс монотонных функций.
Система 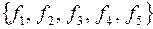 не лежит целиком ни в одном из этих классов, следовательно, по теореме Поста полна в
не лежит целиком ни в одном из этих классов, следовательно, по теореме Поста полна в 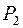 . Чтобы выделить базисы, надо из каждого класса взять функции, которые не лежат в этом классе
. Чтобы выделить базисы, надо из каждого класса взять функции, которые не лежат в этом классе
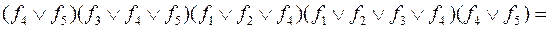
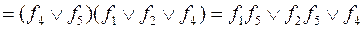 .
.
Базисы: 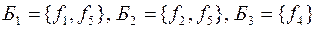 .
.
Задание 9. Построить информативное дерево, усеченное дерево, найти вес функции, построить диаграмму Мура, каноническую таблицу, канонические уравнения автоматной функции после доопределения и минимизации методом Карно для функции 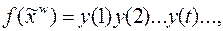 где
где 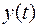 есть
есть 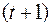 цифра после запятой в двоичном разложении числа
цифра после запятой в двоичном разложении числа 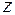
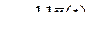 .
.
Если 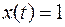 , то
, то 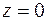 , если
, если 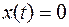 , то
, то 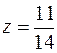 . Получим двоичное разложение дроби. Умножаем дробь на 2, получим
. Получим двоичное разложение дроби. Умножаем дробь на 2, получим 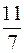 , целая часть равна 1, дробная
, целая часть равна 1, дробная 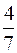 , умножаем ее на 2, получим
, умножаем ее на 2, получим 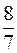 , целая часть равна 1, дробная
, целая часть равна 1, дробная 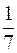 . Умножаем на 2, получим
. Умножаем на 2, получим  , целая часть равна 0, снова умножаем на 2, получим
, целая часть равна 0, снова умножаем на 2, получим 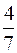 , процесс становится периодическим. Записывая появляющиеся целые части, получаем двоичный код
, процесс становится периодическим. Записывая появляющиеся целые части, получаем двоичный код 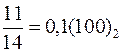 .
.
Построим информативное дерево.

Определим вес функции: очевидно состояние 1~2, 3~4, 7~0, 8~0.
Следовательно, вес функции равен r = 3.
Построим усеченное дерево.
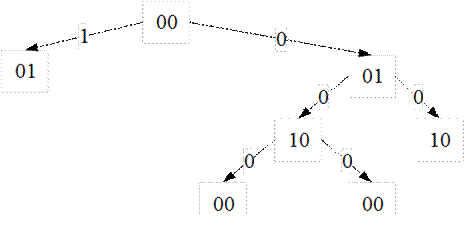
Построим диаграмму Мура
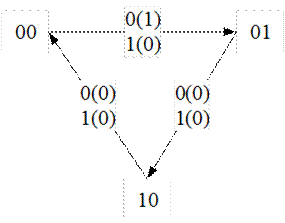
Составим каноническую таблицу.
| x(t) q1(t –1) q2(t–1) | y(t) | q1(t) | q2(t) |
| 0 0 0 | 1 | 0 | 1 |
| 0 0 1 | 0 | 1 | 0 |
| 0 1 0 | 0 | 0 | 0 |
| 0 1 1 | – | – | – |
| 1 0 0 | 0 | 0 | 1 |
| 1 0 1 | 0 | 1 | 0 |
| 1 1 0 | 0 | 0 | 0 |
| 1 1 1 | – | – | – |
Найдем канонические уравнения после доопределения и минимизации методом карт Карно.
Найдем функцию y(t).
| q1(t –1) q2(t–1) | 0 0 | 0 1 | 1 1 | 1 0 |
| x(t) | ||||
| 0 1 | 1 | 0 0 | – – | 0 0 |
| 0 |
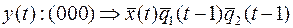
Найдем функцию 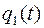 .
.
| q1(t –1) q2(t–1) | 0 0 | 0 1 | 1 1 | 1 0 | ||
| x(t) |
|
| ||||
| 0 1 | 0 0 | 1 1 | – – | 0 0 | ||
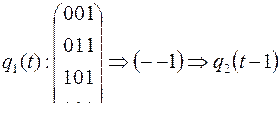
Найдем функцию 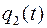 .
.
| q1(t –1) | 0 | 0 | 1 | 1 | ||
| q2(t–1) | 0 | 1 | 1 | 0 | ||
| x(t) |
| |||||
| 0 | 1 | 0 | – | 0 | ||
| 1 | 1 | 0 | – | 0 | ||
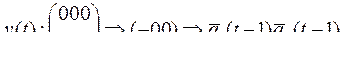
Каноническая таблица после доопределения.
| x(t) q1(t –1) q2(t–1) | y(t) | q1(t) | q2(t) |
| 0 0 0 | 1 | 0 | 1 |
| 0 0 1 | 0 | 1 | 0 |
| 0 1 0 | 0 | 0 | 0 |
| 0 1 1 | 0 | 1 | 0 |
| 1 0 0 | 0 | 0 | 1 |
| 1 0 1 | 0 | 1 | 0 |
| 1 1 0 | 0 | 0 | 0 |
| 1 1 1 | 0 | 1 | 0 |
Записываем каноническое уравнение функции:
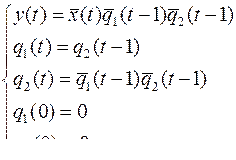
Задание 10. Для суперпозиции 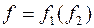 построить информативное дерево, найти вес полученной функции, написать канонические уравнения.
построить информативное дерево, найти вес полученной функции, написать канонические уравнения.
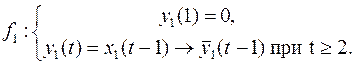
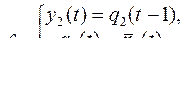
Здесь индекс 1 относится к функции 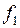 , а индекс 2 – к функции
, а индекс 2 – к функции 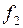 .
.
Приведем функцию 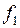 к каноническому виду, для этого построим информативное дерево.
к каноническому виду, для этого построим информативное дерево.

Определим вес функции 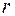 : очевидно состояние
: очевидно состояние 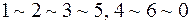 и т. д. Следовательно, вес функции
и т. д. Следовательно, вес функции 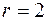 . Построим усеченное дерево.
. Построим усеченное дерево.

Составим каноническую таблицу для 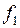 .
.
| x1(t) q1(t –1) | 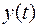
| q1(t) |
| 0 0 | 0 | 1 |
| 0 1 | 1 | 1 |
| 1 0 | 0 | 1 |
| 1 1 | 1 | 0 |
Получим канонические уравнения для функции 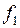 :
:
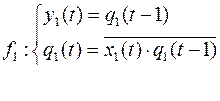
Нарисуем схему суперпозиции 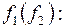
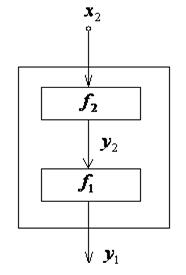
|
Так как 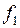 и
и 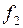 заданы каноническими уравнениями, то вместо
заданы каноническими уравнениями, то вместо 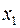 в систему для
в систему для 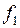 подставим
подставим 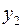 и добавим к системе уравнений
и добавим к системе уравнений 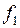 уравнения, задающие состояния автомата
уравнения, задающие состояния автомата 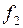 вместе с начальными условиями.
вместе с начальными условиями.
Получим канонические уравнения функции 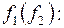
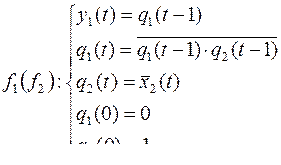
Если вес полученной функции окажется 1 или 2, то уравнения можно упростить. Если вес окажется 3 или 4, то систему уравнений нельзя кардинально упростить.
Найдем вес, построив информативное дерево.
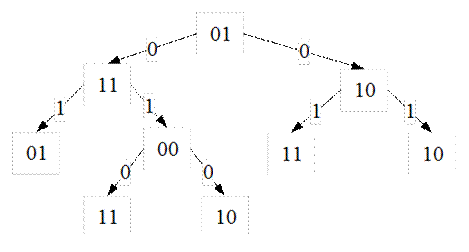
Состояние 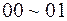 , следовательно, вес функции
, следовательно, вес функции 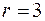 , усеченное дерево выглядит следующим образом:
, усеченное дерево выглядит следующим образом:
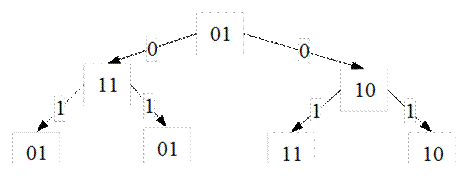
Канонические уравнения для функции 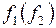 остаются прежними.
остаются прежними.

ЗАКЛЮЧЕНИЕ
Учебное пособие охватывает почти все основные разделы дискретной математики: теорию множеств, комбинаторику, функции алгебры логики, теорию графов, ограниченно-детерминированные функции и схемы из функциональных элементов.
В целом пособие преследует три основные цели:
1. Познакомить читателя с максимально широким кругом понятий дискретной математики, формируя тем самым у студентов терминологический запас, необходимый для самостоятельного изучения специальной математической и теоретико-программистской литературы.
2. Сообщить читателю необходимые конкретные сведения из дискретной математики, предусматриваемые стандартной программой технических высших учебных заведений. Разбор доказательств приведенных утверждений и выполнение упражнений позволяет студенту овладеть методами дискретной математики, наиболее употребительными при решении практических задач.
3. Пополнить запас примеров нетривиальных алгоритмов. Изучение алгоритмов решения типовых задач дискретной математики и способов представления математических объектов в программах абсолютно необходимо практикующему программисту, поскольку позволяет уменьшить трудозатраты на «изобретение велосипеда» и существенно обогащает навыки конструирования алгоритмов.
Дискретная математика имеет широкий спектр приложений, прежде всего в областях, связанных с информационными технологиями и компьютерами. Авторы этого учебного пособия надеются, что оно поможет студентам понять и оценить всю гармонию дискретной математики.
СПИСОК ЛИТЕРАТУРЫ
1. Яблонский C. В. Введение в дискретную математику. М.: Высшая школа, 2003. 384 с.
2. Гаврилов Г. П., Cапоженко A. A. Задачи и упражнения по курсу дискретной математики. М.: Физматлит, 2005.
3. Редькин Н. П. Дискретная математика: Курс лекций для студентов-механиков. CПб.: Изд-во «Лань», 2003.
4. Александров П. C. Введение в теорию множеств и общую топологию / П. C. Александров. М.: ЛКИ, 2008. 368 с.
5. Колмогоров A. Н. Элементы теории функций и функционального анализа / A. Н. Колмогоров, C. В. Фомин. М.: Физматлит, 2006. 572 с.
6. Избранные задачи по вещественному анализу / Б. М. Макаров [и др.]. СПб: Невский диалект, 2004. 624 с.
7. Лавров И. A. Задачи по теории множеств, математической логике и теории алгоритмов / И. A. Лавров, Л. Л. Максимова. М.: Физматлит. 2004. 256 с.
8. Судоплатов C. В., Овчинникова Е. В. Элементы дискретной математики: учебник. М.: ИНФРА-М; Новосибирск: НГТУ, 2003.
9. Плотников A. Д. Дискретная математика: учеб. пособие. М.: Новое знание, 2006.
10. Ахметова Н. A., Усманова З. М. Дискретная математика. Функции алгебры логики: учеб. пособие. Уфа: УГАТУ, 2000. 143 с.
11. Ахметова Н. A., Водопьянов В. В., Кузбеков Т. Т., Усманова З. М. Булева алгебра: учеб. пособие. Уфа: УГАТУ, 2003.
12. Ахметова Н. A., Усманова З. М. Дискретная математика. Теория графов. Схемы из функциональных элементов. Автоматные функции: учеб. пособие. Уфа: УГАТУ, 2009. 108 с.
13. Ахметова Н. A., Гильмутдинова A. Я., Усманова З. М. Элементы дискретной математики. Функции алгебры логики. Теория графов. Элементы теории кодирования: учеб. пособие. Уфа: УГАТУ, 2015. 120 с.
Учебное пособие
ВОДОПЬЯНОВ Владимир Васильевич
АХМЕТОВА Наиля Aбдулхамитовна
ГИЛЬМУТДИНОВА Альфия Ямгутдиновна
УСМАНОВA Зинира Масгутовна
КУРС ДИСКРЕТНОЙ МАТЕМАТИКИ
Редактор Гарипова Ф. Х.
Оформление обложки Южакова М. В.
Подписано в печать 16.04.2018. Формат 60´84 1/16.
Бумага офсетная. Печать плоская. Гарнитура Times New Roman.
Усл. печ. л. 16,0. Уч.-изд. л. 15,9.
Тираж 100 экз. (1-й завод – 1–31 экз.). Заказ №
ФГБОУ ВО «Уфимский государственный авиационный
технический университет»
Редакционно-издательский комплекс УГАТУ
450008, г. Уфа, ул. К. Маркса, д. 12.
Дата: 2019-04-23, просмотров: 646.