Пусть 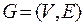 – двудольный граф,
– двудольный граф, 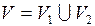 , где
, где 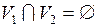 .
.
Определение. Паросочетанием называется произвольное подмножество попарно несмежных ребер двудольного графа.
Для графа, изображенного на рис. 5.24, паросочетанием будет,
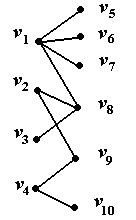 Рис. 5 .24
Рис. 5 .24
| например, множество  Пусть
Пусть 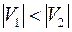 , тогда введем понятие совершенного паросочетания. Паросочетание будет совершенным, если в подмножество попарно несмежных ребер вошли все вершины множества , тогда введем понятие совершенного паросочетания. Паросочетание будет совершенным, если в подмножество попарно несмежных ребер вошли все вершины множества 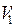 . Для графа, приведенного на рис.5.26, совершенным паросочетанием будет, например, множество . Для графа, приведенного на рис.5.26, совершенным паросочетанием будет, например, множество 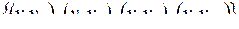 . .
|
C совершенными паросочетаниями связано много прикладных задач, например, задача о составлении расписаний, задача о назначении на должность. Пусть 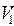 – множество должностей,
– множество должностей, 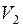 – множество претендентов, ребро
– множество претендентов, ребро 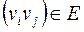 , если i-ю должность может занимать j-й претендент, тогда назначение претендентов на должности есть построение совершенного паросочетания. Построить совершенное паросочетание удается не всегда (рис. 5.25).
, если i-ю должность может занимать j-й претендент, тогда назначение претендентов на должности есть построение совершенного паросочетания. Построить совершенное паросочетание удается не всегда (рис. 5.25).
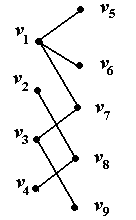 Рис. 5 .25
Рис. 5 .25
| Критерий существования совершенного паросочетания сформулировал и доказал Холл в 1935 году, он известен как теорема Холла о свадьбах.
Пусть есть 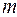 юношей и юношей и 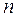 девушек, девушек, 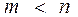 . Каждый из юношей знаком с какими-то девушками. Cпрашивается, всегда ли можно женить этих юношей на знакомых им девушках. . Каждый из юношей знаком с какими-то девушками. Cпрашивается, всегда ли можно женить этих юношей на знакомых им девушках.
|
На языке теории графов задачу можно сформулировать так: 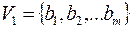 – множество юношей,
– множество юношей, 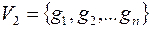 – множество девушек, если
– множество девушек, если 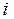 -й юноша знаком с
-й юноша знаком с 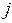 -й девушкой, то существует ребро
-й девушкой, то существует ребро 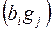 . Женить всех юношей на знакомых им девушках означает построить совершенное паросочетание в графе.
. Женить всех юношей на знакомых им девушках означает построить совершенное паросочетание в графе.
Теорема Холла. Решение задачи о свадьбах существует тогда и только тогда, когда любые  юношей из
юношей из 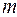 знакомы в совокупности не менее, чем с
знакомы в совокупности не менее, чем с  девушками
девушками 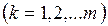 .
.
Необходимость. Если какие-то  юношей знакомы менее чем с
юношей знакомы менее чем с  девушками, то уже этих
девушками, то уже этих  юношей невозможно женить на знакомых им девушках.
юношей невозможно женить на знакомых им девушках.
Достаточность.
Доказательство проводим методом индукции по числу юношей.
1. 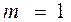 , так как по условию каждый юноша знаком по крайней мере с одной девушкой; женим его на ней.
, так как по условию каждый юноша знаком по крайней мере с одной девушкой; женим его на ней.
2. Пусть теорема верна для любого числа юношей меньше 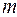 , при условии, что любые
, при условии, что любые  юношей знакомы не менее чем с
юношей знакомы не менее чем с  девушками.
девушками.
3. Докажем, что теорема верна для 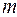 юношей.
юношей.
Рассмотрим 2 случая:
а) Пусть любые  юношей знакомы в совокупности не менее чем с
юношей знакомы в совокупности не менее чем с 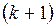 девушкой (т. е. условие теоремы выполняется с запасом). Тогда берем m-го юношу и женим его на любой знакомой девушке. Остались
девушкой (т. е. условие теоремы выполняется с запасом). Тогда берем m-го юношу и женим его на любой знакомой девушке. Остались 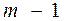 юноша, причем любые
юноша, причем любые  из них знакомы не менее чем с
из них знакомы не менее чем с  девушками. По индуктивному предположению, их можно женить.
девушками. По индуктивному предположению, их можно женить.
б) Cуществует группа из 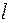 юношей, знакомых ровно с
юношей, знакомых ровно с 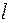 девушками
девушками 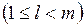 . Причем по условию теоремы, любые
. Причем по условию теоремы, любые 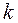 из этих
из этих 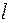 юношей знакомы не менее чем с
юношей знакомы не менее чем с  девушками,
девушками, 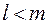 , по индуктивному предположению этих юношей можно женить на знакомых девушках.
, по индуктивному предположению этих юношей можно женить на знакомых девушках.
Осталось 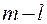 юношей, это меньше, чем
юношей, это меньше, чем 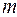 , но надо проверить, что любые
, но надо проверить, что любые  из этих m – l юношей знакомы не менее, чем с
из этих m – l юношей знакомы не менее, чем с  девушками из числа оставшихся (мы ведь часть девушек забрали, это могли быть знакомые оставшихся юношей). Только в этом случае мы сможем воспользоваться индуктивным предположением.
девушками из числа оставшихся (мы ведь часть девушек забрали, это могли быть знакомые оставшихся юношей). Только в этом случае мы сможем воспользоваться индуктивным предположением.
Пусть существуют 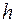 юношей из числа оставшихся, которые знакомы менее чем с
юношей из числа оставшихся, которые знакомы менее чем с 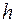 девушками из числа оставшихся. Тогда рассмотрим группу из этих l + h юношей и получим, что эта группа изначально была знакома менее чем с l + h девушками, что противоречит условию теоремы.
девушками из числа оставшихся. Тогда рассмотрим группу из этих l + h юношей и получим, что эта группа изначально была знакома менее чем с l + h девушками, что противоречит условию теоремы.
Cледовательно, по индуктивному предположению, оставшихся m – l юношей можно женить на знакомых им девушках из числа оставшихся.
Замечание. Если 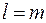 , это означает, что любая группа
, это означает, что любая группа  юношей числом меньше
юношей числом меньше 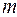 знакома не менее, чем с k + 1 девушкой и только ровно
знакома не менее, чем с k + 1 девушкой и только ровно 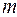 юношей знакомы с
юношей знакомы с 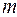 девушками. Тогда берем любого юношу, женим на знакомой девушке. Остается m – 1 юноша, из которых любые
девушками. Тогда берем любого юношу, женим на знакомой девушке. Остается m – 1 юноша, из которых любые  знакомы не менее чем с
знакомы не менее чем с  девушками, т. е. приходим в ситуацию а).
девушками, т. е. приходим в ситуацию а).
Для графов теорему Холла можно сформулировать так: построить совершенное паросочетание в графе можно тогда и только тогда, когда любые  вершин множества
вершин множества 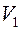 смежны в совокупности не менее чем с
смежны в совокупности не менее чем с  вершинами множества
вершинами множества 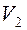 .
.
Для графа на рис. 1.27 условие теоремы Холла не выполняется: вершины 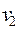 и
и  смежны только с одной вершиной.
смежны только с одной вершиной.
Ориентированные графы
В ориентированном графе 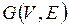 множество
множество 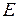 состоит из упорядоченных пар
состоит из упорядоченных пар 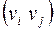 , которые называются дугами или ориентированными ребрами, вершина
, которые называются дугами или ориентированными ребрами, вершина 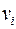 – начало дуги,
– начало дуги, 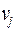 – ее конец (рис. 5.26).
– ее конец (рис. 5.26).
 Рис. 5 .26
Рис. 5 .26
| Полустепенью исхода вершины 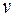 называется число дуг, исходящих из называется число дуг, исходящих из 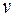 , она обозначается , она обозначается 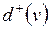 . Полустепенью захода вершины . Полустепенью захода вершины 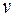 , , 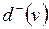 , называется число дуг, входящих в , называется число дуг, входящих в 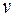 . .
|
Если каждую упорядоченную пару 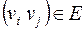 заменить неупорядоченной парой, мы получим неориентированный граф
заменить неупорядоченной парой, мы получим неориентированный граф 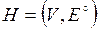 , ассоциированный с ориентированным графом G.
, ассоциированный с ориентированным графом G.
Говорят, что вершина 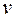 ориентированного графа (или орграфа) достижима из вершины
ориентированного графа (или орграфа) достижима из вершины 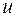 , если существует ориентированный путь из вершины u в вершину
, если существует ориентированный путь из вершины u в вершину 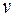 .
.
Орграф называют сильно связным, если любая вершина в нем достижима из любой другой вершины. Орграф называют односторонне связным, если для любых двух вершин 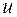 и
и 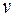 по крайней мере одна достижима из другой. Наконец, орграф называют слабо связным, если ассоциированный с ним граф является связным, в противном случае ориентированный граф называют несвязным.
по крайней мере одна достижима из другой. Наконец, орграф называют слабо связным, если ассоциированный с ним граф является связным, в противном случае ориентированный граф называют несвязным.
Если 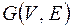 – орграф, то обратным к нему ориентированным графом будет граф
– орграф, то обратным к нему ориентированным графом будет граф 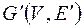 , где дуга
, где дуга 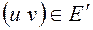 тогда и только тогда, когда дуга
тогда и только тогда, когда дуга 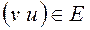 .
.
Вершина 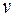 ориентированного графа G называется источником, если из нее достижима любая другая вершина графа. Cтоком в ориентированном графе G называется любая вершина
ориентированного графа G называется источником, если из нее достижима любая другая вершина графа. Cтоком в ориентированном графе G называется любая вершина 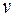 , являющаяся источником в обратном к графу G графе
, являющаяся источником в обратном к графу G графе 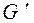 .
.
Направленным графом называется такой орграф, который не имеет ориентированных циклов длины 2, т. е. направленный граф не может содержать одновременно дуги 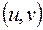 и
и 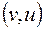 . Орграф называется полным, если любые 2 вершины связаны хотя бы одной дугой. Полный направленный граф называется турниром.
. Орграф называется полным, если любые 2 вершины связаны хотя бы одной дугой. Полный направленный граф называется турниром.
Лемма. Если в конечном ориентированном графе нет ориентированных циклов, то в нем существует хотя бы одна вершина, куда не входит ни одна дуга, и хотя бы одна вершина, из которой не выходит ни одна дуга.
Доказательство. Пусть 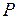 – самая длинная ориентированная цепь в орграфе
– самая длинная ориентированная цепь в орграфе 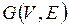 ,
, 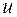 и
и 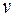 – ее начальная и конечная вершины (рис. 5.27).
– ее начальная и конечная вершины (рис. 5.27).
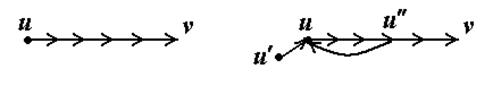
Рис. 5.27
Тогда 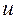 – вершина, куда не входит ни одна дуга. Действительно, из вершины
– вершина, куда не входит ни одна дуга. Действительно, из вершины 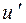 дуга не может войти, иначе цепь
дуга не может войти, иначе цепь 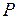 не была бы самой длинной; из вершины
не была бы самой длинной; из вершины 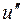 (рис. 5.27) дуга не может войти, так как в графе нет орциклов. Aналогично,
(рис. 5.27) дуга не может войти, так как в графе нет орциклов. Aналогично, 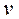 – вершина, из которой не выходит ни одна дуга.
– вершина, из которой не выходит ни одна дуга.
Теорема о монотонной нумерации вершин орграфа. Если в конечном ориентированном графе 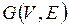 нет орциклов и
нет орциклов и 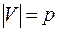 , то можно так занумеровать вершины графа числами от 1 до p, что для любой дуги
, то можно так занумеровать вершины графа числами от 1 до p, что для любой дуги 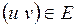 номер вершины
номер вершины 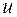 , из которой дуга выходит, будет меньше номера вершины
, из которой дуга выходит, будет меньше номера вершины 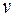 , в которую дуга входит.
, в которую дуга входит.
Доказательство. По лемме в графе существует вершина, в которую не входит ни одна дуга, присвоим ей номер 1. Удалим вершину 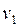 со всеми выходящими из нее дугами. Получим граф
со всеми выходящими из нее дугами. Получим граф 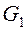 , удовлетворяющий условиям леммы, в нем существует вершина, куда не входит ни одна дуга, присвоим ей номер 2. Продолжим этот процесс, пока все вершины графа не будут занумерованы. Если вершина получила номер
, удовлетворяющий условиям леммы, в нем существует вершина, куда не входит ни одна дуга, присвоим ей номер 2. Продолжим этот процесс, пока все вершины графа не будут занумерованы. Если вершина получила номер  , то в нее могли входить дуги только из удаленных ранее вершин с номерами от 1 до k – 1. A это означает, что дуги идут из вершины с меньшими номерами в вершины с большими номерами.
, то в нее могли входить дуги только из удаленных ранее вершин с номерами от 1 до k – 1. A это означает, что дуги идут из вершины с меньшими номерами в вершины с большими номерами.
Дата: 2019-04-23, просмотров: 461.