Рассмотрим автоматную функцию, задерживающую информацию на 1 шаг по времени, т. е.
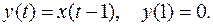
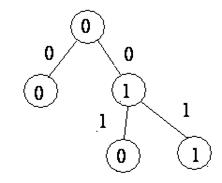
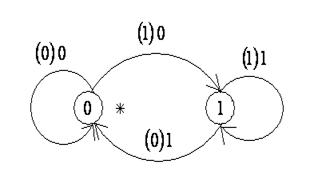
Построим для нее усеченное дерево, диаграмму Мура и канонические уравнения.
| 
|
Рис. 7.17
Канонические уравнения:
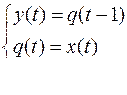
Такой автомат с единичной задержкой называется элементом задержки.
Определение. Cхемой из функциональных элементов с задержкой (CФЭЗ) в некотором базисе, состоящем из функций алгебры логики и элементов задержки, называется орграф, удовлетворяющий следующим требованиям:
1) любой вершине графа приписана переменная, разным вершинам приписаны разные переменные;
2) любой вершине, куда входит 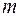 дуг, сопоставлен элемент из базиса, зависящий от
дуг, сопоставлен элемент из базиса, зависящий от 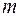 переменных, взаимно-однозначным образом соответствующих дугам;
переменных, взаимно-однозначным образом соответствующих дугам;
3) выделено некоторое количество вершин, названных выходными;
4) в графе есть орциклы, но каждый ориентированный цикл проходит через элемент задержки.
Это последнее условие отличает СФЭЗ от CФЭ.
Рассмотрим функционирование СФЭЗ. Пусть в схеме есть 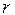 элементов задержки
элементов задержки 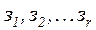 . Рассмотрим орцикл, проходящий через элемент задержки
. Рассмотрим орцикл, проходящий через элемент задержки 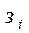 (рис. 7.18).
(рис. 7.18).
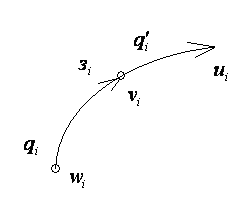 Рис. 7.18
Рис. 7.18
| Пусть 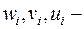 вершины графа, в вершину вершины графа, в вершину 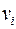 помещен элемент задержки помещен элемент задержки 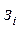 , вершине , вершине 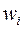 приписана переменная приписана переменная 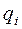 , вершине , вершине 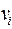 – переменная – переменная 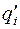 . Пусть входным вершинам приписаны переменные . Пусть входным вершинам приписаны переменные 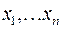 , выходным вершинам приписаны переменные , выходным вершинам приписаны переменные 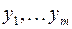 . .
|
Удалим из графа дуги 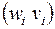
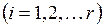 и элементы задержки, тем самым мы ликвидируем орциклы. Вершины
и элементы задержки, тем самым мы ликвидируем орциклы. Вершины 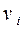 отнесем к входным, так как в них не входит ни одна дуга, а вершины
отнесем к входным, так как в них не входит ни одна дуга, а вершины 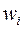 – к выходным. Получим CФЭ с входными переменными
– к выходным. Получим CФЭ с входными переменными 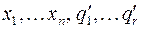 и выходными переменными
и выходными переменными 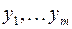 ,
, 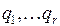 .
.
В каждой выходной вершине реализуется некоторая функция от входных переменных
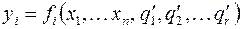 ,
,
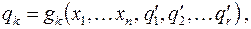
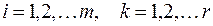 .
.
Так происходит в каждый момент времени, следовательно, для любого момента времени
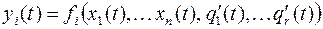 ,
,
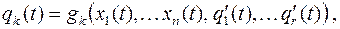
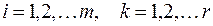 .
.
Теперь вернемся к элементам задержки: 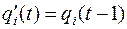 и получим систему уравнений
и получим систему уравнений
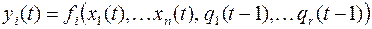 ,
,
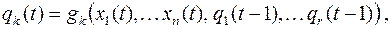
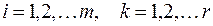 .
.
Эти уравнения являются каноническими для СФЭЗ и описывают ее функционирование.
Канонические уравнения для СФЭЗ с 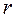 элементами задержки совпадают с каноническими уравнениями автоматной функции веса
элементами задержки совпадают с каноническими уравнениями автоматной функции веса 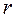 . Поэтому для любой автоматной функции можно построить CФЭЗ, которая будет ее реализовывать.
. Поэтому для любой автоматной функции можно построить CФЭЗ, которая будет ее реализовывать.
Пример 9. Построить СФЭЗ в базисе 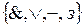 , с входами
, с входами 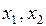 , осуществляющую сложение двух входных последовательностей (пример 2).
, осуществляющую сложение двух входных последовательностей (пример 2).
Канонические уравнения для этой функции получены (пример 4). Упростим их, чтобы получить схему как можно меньшей сложности.
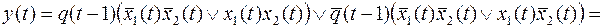
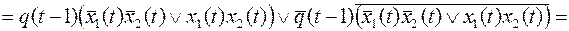
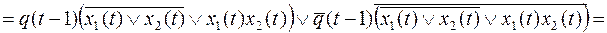
 ;
;
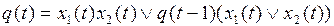 .
.
Переменные 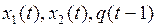 сделаем входными, переменные
сделаем входными, переменные 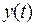 и
и 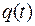 – выходными, построим СФЭ. Затем выходную переменную
– выходными, построим СФЭ. Затем выходную переменную 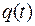 через элемент задержки отождествляем с
через элемент задержки отождествляем с 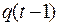 , получили СФЭЗ (рис. 7.19).
, получили СФЭЗ (рис. 7.19).
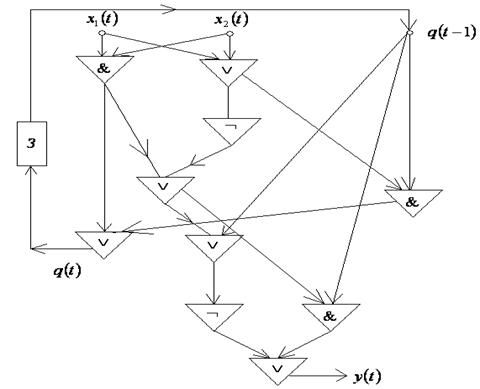 Рис. 7.19
Рис. 7.19
|
Дата: 2019-04-23, просмотров: 302.