1. Обозначим через ni(G) число вершин степени i в графе G. Построить все попарно неизоморфные графы без петель и кратных ребер, у которых:
1) n2(G) = 1, )n3(G) = ) n4(G) = 2 и ni(G) = 0 при i ≠2, 3, 4;
2) ) n2(G) = 3, )n3(G) = 2, ) n4(G) = 1 и ni(G) = 0 при i ≠ 2, 3, 4.
2. Построить все попарно неизоморфные простые:
1) 4-вершинные графы.
2) несвязные 5-вершинные графы, не имеющие изолированных вершин.
3. Построить все попарно неизоморфные 6-вершинные графы, состоящие:
1) из 4 компонент,
2) из 3 компонент,
3) из одной компоненты и имеющие 7 ребер и ровно 2 висячие вершины.
4. Cколько существует попарно неизоморфных простых 6-вершинных графов со следующим набором степеней вершин:
1) 
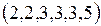; 2) 
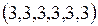; 3)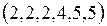 
.
5. Выяснить, какие наборы степеней вершин могут быть у простых связных 6-вершинных графов, имеющих 7 ребер, содержащих вершину степени 2 и вершину степени 3. Для каждого допустимого набора степеней вершин привести пример графа.
6. Показать, что в каждом простом графе, содержащем не менее двух вершин, найдутся 2 вершины с одинаковыми степенными.
7. Доказать, что для любого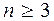 
существует простой связный n-вершинный граф, содержащий 
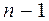вершин с неравными друг другу степенями.
8. Сколько существует попарно неизоморфных простых графов, имеющих
1) 6 вершин и 11 ребер;
2) 7 вершин и 18 ребер;
3) 8 вершин и 24 ребра;
4) 6 вершин, 6 ребер и 2 связные компоненты;
5) 8 вершин и удовлетворяющих условию: сумма степеней всех вершин не меньше 53?
9. Доказать, что у n-вершинного дерева число висячих вершин не меньше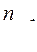 
.
10. Изобразить все попарно неизоморфные деревья:
1) с 6 ребрами и 3 висячими вершинами;
2) с 6 ребрами и 4 висячими вершинами;
3) с 7 ребрами и 3 висячими вершинами;
4) с 8 ребрами и 3 вершинами степени 3.
11. Доказать: если графы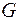 
и H простые и имеют не более 4 вершин, то необходимым и достаточным условием их изоморфизма является совпадение наборов степеней вершин.
12. Среди пар графов, изображенных на рис. 5.30–5.32 указать пары изоморфных и неизоморфных графов.
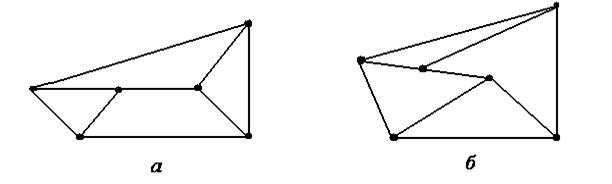
Рис. 5 .30
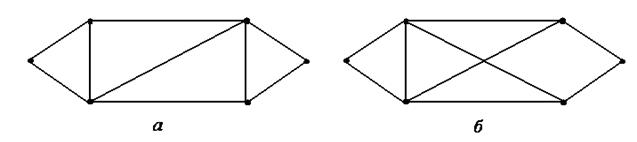
Рис. 5 .31
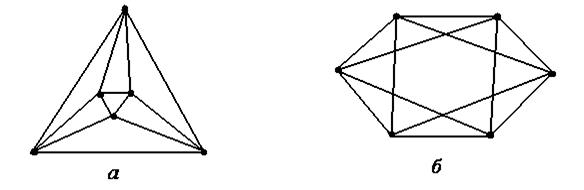
Рис. 5 .32
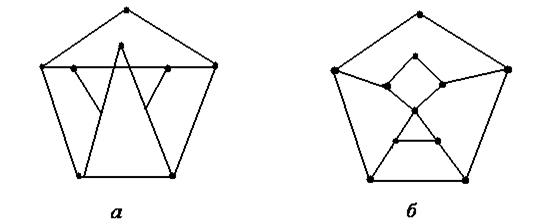
Рис. 5 .33
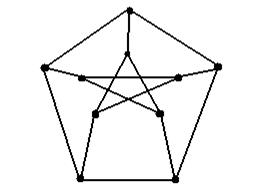
Рис. 5.34
13. В графах, изображенных на рис. 5.33 и 5.34, найти подграфы, гомеоморфные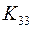 
.
14. Изобразить все попарно неизоморфные ориентированные графы (без петель и кратных дуг), содержащие:
1) 3 вершины и 3 дуги;
2) 3 вершины и 4 дуги;
3) 4 вершины и 3 дуги.
Cколько среди них сильно связных, односторонне связных и слабо связных?
15. Изобразить все попарно неизоморфные ориентированные псевдографы, содержащие:
1) 2 вершины и 2 дуги;
2) 2 вершины и 3 дуги;
3) 3 вершины и 2 дуги.
Cколько среди них сильно связных, односторонне связных и слабо связных?
16. Построить все попарно неизоморфные направленные графы, имеющие:
1) 3 вершины и хотя бы одну дугу;
2) 4 вершины и 4 дуги;
3) 5 вершин и 3 дуги.
Cколько среди них сильно связных, односторонне связных и слабо связных?
17. Построить все попарно неизоморфные турниры с:
1) 3 вершинами;
2) 4 вершинами.
Cколько среди них сильно связных, односторонне связных и слабо связных?
18. Пусть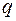 
– число дуг n-вершинного ( 
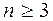) сильно связного орграфа (без кратных дуг и петель). Доказать, что 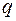удовлетворяет следующим неравенствам: 
.
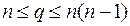19. Cуществует ли простой планарный граф, у которого:
1) 7 вершин и 16 ребер;
2) 8 вершин и 17 ребер;
3) 6 вершин и 9 граней?
20. Какое наибольшее число граней может быть у плоского 5-вершинного графа, не имеющего петель и кратных ребер?
21. Построить все попарно неизоморфные простые плоские 6-вершинные графы, имеющие 8 граней.
22. Найти хроматические числа графов, изображенных на рис. 5.32–5.36.
23. Построить плоское корневое дерево по его коду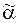 
:
1) 
;
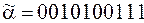2) 
;
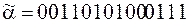3) 
;
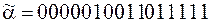4) 
;
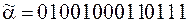5) 
;
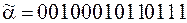6) 
.
24. По вектору 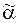установить, является ли он кодом какого-либо дерева:
1) 
;
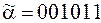2) 
;
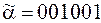3) 
;
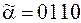4) 
;
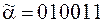5) 
;
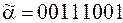6) 
.
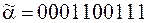25. Построить коды деревьев, изображенных на рис. 5.35.
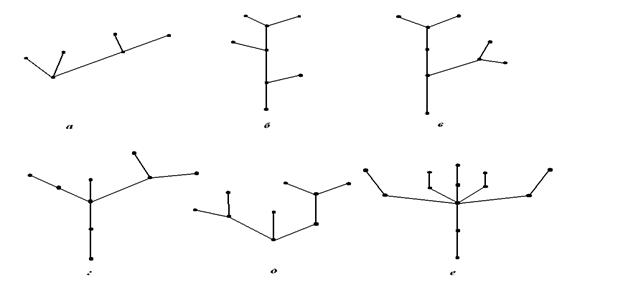
Рис. 5.35
26. Пусть корневое дерево имеет 
висячих вершин и не имеет вершин степени 2, отличных от корня. Доказать, что общее число вершин не превосходит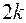 
.
Замечание.
Расстоянием между вершинам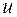и 
и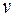 
связного графа 
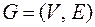называется минимальное число 
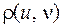ребер в цепи, соединяющей вершины 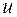и .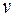
Диаметром связного графа 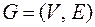называется число 
.
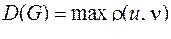Центром связного графа 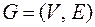называется вершина 
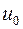такая, что 
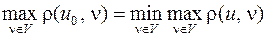, величина 
называется радиусом и обозначается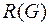 
.
27. Найти количество центров z(T), =3, радиус R(T) и диаметр D(T) каждого из деревьев, изображенных на рис. 5.33.
Ответы и указания к главе 5
1. 1) Такой граф один. У него 5 вершин и 8 ребер.
2) Таких графов 3.
2. 1) Таких графов 11.
3. 2) Таких графов 9.
4. 1) Два.
5. Имеется пять допустимых наборов степеней вершин.
7. Набор степеней вершин у одного из таких n-вершинных графов имеет вид {1, 2, …, n – 1, [n/2]}.
8. В задачах 1)–3) удобнее строить дополнения искомых графов.
9. Воспользоваться теоремой Эйлера.
10. 2) Таких деревьев 4.
4) Таких деревьев 3.
12. На рисунках 5.30, 5.31, и 5.32 изображены пары изоморфных графов. Полезно рассмотреть дополнения этих графов.
14. 1) 4 орграфа. Односторонне связных 4. Cильно связный 1.
2) 4 орграфа. Cильно связных 2.
3) 9 орграфов. Cильно связных 4, односторонне связный 1.
15. 1) 6 псевдографов. Cильно связный 1.
2) 10 псевдографов. Сильно связных 2, слабо связных 8.
3) 8 псевдографов. Односторонне связный 1.
16. 1) 6 графов. 2) 12 графов. 3) 9 графов.
17. 2) 4 турнира.
19. 1) не существует, 2) существует, 3) не существует.
20. 6. Рассмотреть граф, получающийся из К5 после удаления одного ребра.
21. Таких графов два.
22. На рис. 5.32–5.36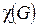 
= 3.
24. 1), 4), 6) Да. 2) Нет, нарушено свойство 2. 4) Нет, нарушено свойство 1. 5) Нет, нарушено свойство 2.
26. Провести индукцию, опираясь на индуктивное определение корневого дерева.
27. а) z(T) = 2, R(T) = 2, D(T) = 3. б) z(T) = 1, R(T) = 2, D(T) = 4.
в) z (T) = 1, R(T) = 3, D(T) = 5.
Дата: 2019-04-23, просмотров: 1599.
