Ориентированный граф, у которого некоторые вершины выделены, называется сетью, выделенные вершины называются полюсами. Например, корневое дерево может рассматриваться как однополюсная сеть.

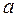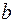Мы будем рассматривать двухполюсные сети с полюсами  и , полюс  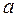назовем входом, полюс  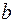– выходом, сеть будем обозначать 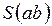. Вершины, отличные от полюсов, называются внутренними вершинами. Ребро, инцидентное хотя бы одному полюсу, называется полюсным ребром, остальные ребра называются внутренними.

Будем предполагать, что ассоциированный с сетью граф связен и не содержит кратных ребер и петель.

Пусть каждому ориентированному ребру 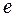 графа приписано неотрицательное число  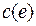– пропускная способность. Потоком в сети  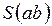называется числовая функция 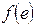, заданная на множестве всех дуг, удовлетворяющая следующим требованиям:

1)

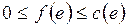
2) 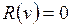 для всех внутренних вершин, где 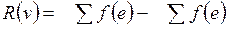;  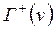– множество всех дуг, исходящих из v (для них v – начальная вершина),  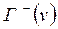– множество всех дуг, входящих в v.

Замечание. В электрических сетях последнее требование называется законом Кирхгофа.

Так как каждое ребро является входящим в одну вершину и исходящим для другой, то 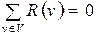, откуда .

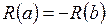Значение 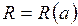 называется величиной потока.

Обозначим 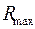 – максимальную величину потока в сети при заданных пропускных способностях.

Поставим задачу нахождения .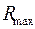

Определение. Сечением сети называется множество ребер, удаление которых делает ассоциированный граф несвязным, причем полюсы попадают в разные компоненты связности. Ясно, что каждая простая цепь 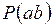 в ассоциированном графе должна проходить хотя бы через одно ребро сечения.

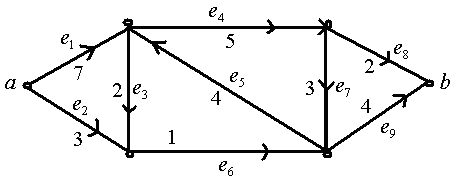
Рис. 5.28

В сети на рис. 5.28 примерами сечений являются , , .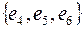

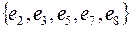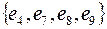Cечение называется простым, если при удалении любого его ребра оно перестает быть сечением. Так 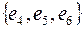 и 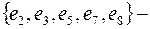простые сечения, а последнее не является таковым, можно из него убрать  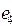и 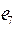,  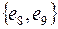образуют сечение, которое будет простым. Очевидно, для каждого ребра простого сечения можно указать простую цепь  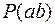в ассоциированном графе, которая проходит через данное ребро и не проходит через другие ребра этого сечения.

Замечание. Далее простую цепь в ассоциированном графе будем называть псевдоцепью.

Лемма о распаде сети. Если в связной сети удаляется простое сечение, то сеть распадается на две связные компоненты: содержащую вершину a, назовем ее левой, и содержащую вершину b, назовем ее правой.

Доказательство. Надо доказать, что при удалении простого сечения W ассоциированный граф распадается ровно на 2 связные компоненты: левую и правую.

Пусть 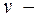произвольная вершина, надо показать, что она останется связанной псевдоцепью либо с вершиной 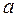, либо с вершиной .

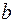Пусть 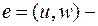ребро, принадлежащее W, соединим  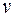псевдоцепью  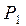с вершиной  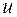так, чтобы  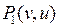не содержало концов ребер, входящих в W, это возможно в силу связности графа (рис. 5.29)

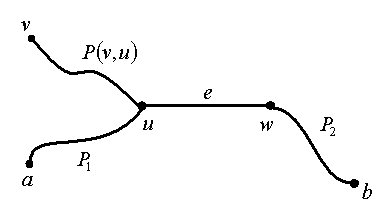
Рис. 5.29

Так как 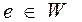, то существует простая цепь 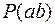, проходящая только через это ребро простого сечения:

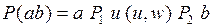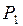, где  и 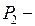последовательности ребер и вершин, не содержащие концов ребер из простого сечения.

Возможны 2 варианта:

1) 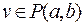, пусть 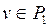, тогда  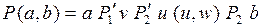и при удалении ребра  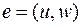вершина 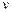окажется связанной с полюсом a (или 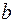, если ).

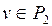2) 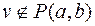, но тогда при удалении ребра  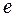вершина  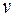будет связана с 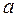псевдоцепью 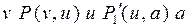, которая не содержит концов ребер из W.

Cогласно лемме, каждое ребро простого сечения связывает вершины из двух частей: левой и правой. Будем называть ребро прямым, если оно в сечении ориентировано слева направо (т. е. поток по нему идет из вершины 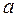в вершину ).

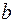Каждому простому сечению W припишем пропускную способность 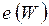, которая равна сумме пропускных способностей его прямых ребер. В примере (рис. 5.28) сечение  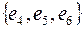имеет пропускную способность 5 + 1 = 6, а сечение  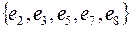имеет пропускную способность 3 + 2 + 3 + 2 = 10.

Теорема Форда и Фалкерсона. Максимальная величина потока 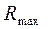 через сеть S равна минимальной из пропускных способностей  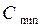ее простых сечений: .

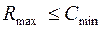Доказательство. Докажем сначала, что для любого потока и любого сечения .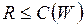

Просуммируем 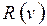 по всем вершинам левой относительно сечения W  компоненты сети.

.

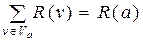C другой стороны, она равна сумме потоков, идущих по прямым ребрам сечения, минус сумма потоков, идущих по обратным ребрам сечения.

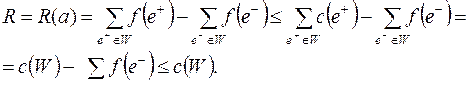
Здесь через 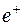 обозначены прямые ребра сечений 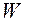, 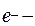обратные.

Так как поток и сечение были произвольные, то отсюда следует, что .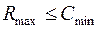

Доказательство того, что в сети можно создать поток величины 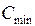 мы приводить не будем.