Решение уравнений кинетики с учетом всех групп запаздывающих нейтро­нов является довольно громоздким. Некоторое представление об относительной значимости установившегося и переходных членов уравнения (12.38) можно получить, рассматривая простой случай, когда имеется только одна группа за­паздывающих нейтронов, характеризуемых постоянной распада λ. Величину λ определим как средневзвешенное значение по всем группам запаздывающих нейтронов. Для случая одной группы запаздывающих нейтронов уравнение (12.36) принимает вид

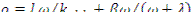                                                                                         (12.43)

где 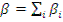  - суммарная доля запаздывающих нейтронов;  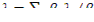- среднее значение постоянной распада осколков деления, излучающих запаздываю­щие нейтроны.

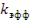Для реактора, работающего на тепловых нейтронах, в котором в качестве делящегося изотопа используется U²³⁵, суммарная доля запаздывающих ней­тронов =0,0064, а постоянная распада λ=0,077 с^-1 . Для упрощения дальнейших преобразований положим, что реактивность ρ настолько мала, что ≈1. То­гда уравнение (12.43) запишется так:

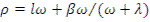                                                                                                     (12.44)

Полученное уравнение является квадратным уравнением относительно 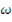 и может быть записано следующим образом:

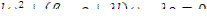
Отсюда

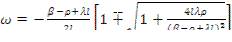                                                                                (12.45)

Корень квадратный вида 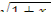при 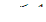 можно разложить в ряд Тейлора

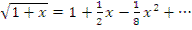
Если принять l=10^-3 с, ρ=0,003, то 4lλ р =4 10^-3 0,077 0,003 = 0,925 10^-6, откуда

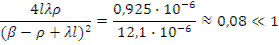
Тогда, ограничившись в разложении двумя первыми членами, выражение (12.45) можно представить в следующем виде:

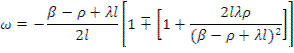
Отсюда

При определении 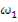 пренебрегли вторым членом в квадратных скобках по сравнению с единицей. Если учесть теперь, что  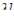=0,077 10^-3 , а

β—ρ=0,0064-0,0030=0,034 10^-1 , то произведением 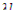 по сравнению с (β-ρ) также можно пренебречь, и решение относительно со окончательно будет иметь вид

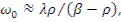                                                                                                           (12.46)                                                                                                                                                                                                                                                                                                                                                                                                                         

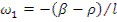                                                                                                            (12.47)

При положительном скачке реактивности и (β-ρ)>0 значение 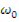 положи­тельно, а  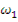 отрицательно.

Выражение (12.38), описывающее изменение плотности нейтронного потока во времени, с учетом одной средневзвешенной группы запаздывающих нейтро­нов примет вид

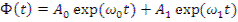                                                                               (12.48)

а концентрация предшественников запаздывающих нейтронов в соответствии с (12.31) будет выражаться соотношением

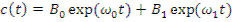                                                                                 (12.49)

Коэффициенты А и В в (12.48) и (12.49) являются постоянными интегриро­вания и определяются из начальных условий.

С учетом одной группы запаздывающих нейтронов уравнение (12.13).при­нимает вид

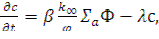                                                                                           (12.50)

в котором связаны величины Ф и с.

Подставляя в (12.50) вместо Ф и с их выражения, согласно (12.48) и (12.49), получаем

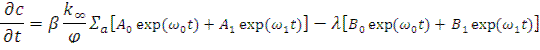
Дифференцируя теперь выражение (12.49), будем иметь

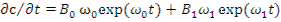
Из сравнения последних двух уравнений видно, что правые части их будут равны, если приравнять соответствующие коэффициенты при одинаковых экс­понентах:

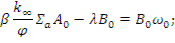
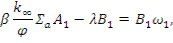
отсюда коэффициенты B ₀ и B₁будут равны:

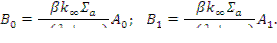
Подставляя в эти выражения вместо 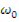 и 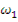 их значения в соответствии с (12.46) и (12.47) и пренебрегая величиной  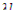по сравнению с величиной (β-ρ),

получаем:

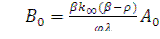                                                                                           (12.51)

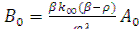                                                                                               (12.52)

Как видно из формул (12.51) и (12.52), связь между соответствующими по­стоянными А и В выражается посредством величин, определяющихся свойст­вами данного реактора, поэтому остается определить только две произвольные постоянные. Для этой цели требуются два начальных условия.

Условия в момент времени t =0 в соответствии с (12.48) и (12.49):        

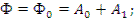                                                                                                       (12.53)                                                                                                                                                                                                                                                                                                                                                                                                                                                            

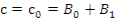                                                                                                              (12.54)

где Ф₀ и c₀ — соответственно плотность потока нейтронов и концентрация предшественников запаздывающих нейтронов до внесения возмущения.

Для нахождения связи между Ф₀ и c ₀ , учитывая, что при условии стацио­нарной работы реактора концентрация предшественников не должна меняться со временем, потребуем, чтобы в момент времени t =0 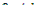 = 0 или, соглас­но (12.50),

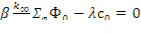                                                                                                   (12.55)

Из уравнения (12.55) следует, что

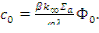                                                                                                                 (12.56)                                                                                                    

Подставив теперь в (12.54) вместо c₀ его выражение из (12.56), а вместо B₀ и B₁ - их выражения в соответствии с (12.51) и (12.52), будем иметь

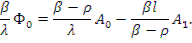
Используя (12.53), заменим в последнем выражении А₁  на (Ф₀ — A ₀ ). Тогда

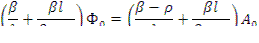
Второй член в скобках правой и левой частей, 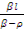, имеющий порядок

10^-3 , мал по сравнению с первыми, имеющими порядок 10^-1 , и им можно пре­небречь. С учетом этого:

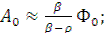                                                                                               (12.57)

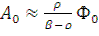                                            .                                             (12.58)                                     

Подставив этот результат, а также (12.46) и (12.47) в выражение (12.48), по­лучим формулу для плотности нейтронного потока в зависимости от времени

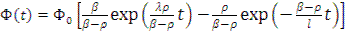                                                (12.59)

При положительном значении ρ и β-ρ>0 плотность нейтронного потока представляет собой разность двух членов, из которых положительный член растет со временем, а отрицательный быстро падает.

Для иллюстрации подставим в формулу (12.59) численные значения величин. Предположим, как и ранее, что l=10^-3 с, ρ=0,003, β=0,0064, λ=0,077 с^-1 , тогда

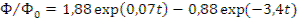                                                             (12.60)                                                                                                                                                                                                                                                                                                           

На рис. 12.3 сплошной линией показано изменение отношения Ф/Ф₀ по формуле (12.60). На этом же рисунке пунктирными линиями показано измене­ние каждого члена правой части формулы (12.60) в отдельности.

Кривая 1 соответствует изменению первого члена, а кривая 2 — изменению второго. Из рисунка видно, что второй член очень быстро убывает и в данном случае уже к исходу первой секунды вклад его составляет около 0,2% и им можно пренебречь. Поэтому по истечении очень малого промежутка времени (порядка секунды) изменение плотности нейтронного потока практически оп­ределяется первым членом, и можно записать, что

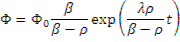
Из последнего выражения следует, что установившийся период реактора равен

                                                    (12.62)

Если подставить численные значения β, λ и ρ, которые использовались ра­нее, то получим

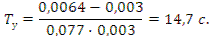
 Установившийся период реактора с уче­том запаздывающих нейтронов составляет 14,7 с. Для этих же условий, но без учета за­паздывающих нейтронов период равен 0,33 с. Таким образом, переходный процесс будет идти значительно медленней, чем без учета запаздывающих нейтронов.

При очень малых значениях реактивности (порядка сотых долей процента) в формуле (12.62) величиной р по сравнению с величи­ной ρ можно пренебречь и установившийся период реактора будет обратно пропорциона­лен реактивности

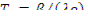
Величина 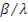 представляет собой средне­взвешенное время жизни запаздывающих нейтронов τ_зн , т.е.

Это выражение аналогично формуле (12.12), только вместо времени жизни мгновенных нейтронов здесь фигурирует время жизни запаздывающих нейтро­нов. Поэтому установившийся период реактора полностью определяется свой­ствами запаздывающих нейтронов.

Период реактора является очень важной эксплуатационной характеристикой и всегда контролируется в процессе работы аппарата, в особенности во время пуска реактора. Величина 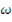, обратная периоду реактора, представляет собой скорость разгона аппарата. Чем больше период, тем меньше скорость разгона, и наоборот, с уменьшением периода реактора скорость разгона возрастает. При больших значениях реактивности период реактора мал и скорость разгона мо­жет оказаться настолько большой, что управление реактором будет невозмож­но. Если значение , то запаздывающие нейтроны практически не оказы­вают влияния на переходный процесс.

Вводится понятие так называемой мгновенной критичности [2], которая соответствует состоянию 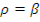. Это значит, что реактор критичен уже по отно­шению только к мгновенным нейтронам. А так как наряду с генерацией мгновенных нейтронов идет генерация и запаздывающих нейтронов, то реактор в целом надкритичен с положительной реактивностью 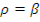, и разгон его идет очень быстро с периодом, определяемым мгновенными нейтронами. Таким об­разом, значение ρ всегда должно оставаться меньше β.

При положительном скачкообразном изменении реактивности и 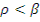 плот­ность нейтронного потока в первый момент времени после внесения возмуще­ния быстро возрастает, а затем скорость изменения плотности потока переходит постепенно к скорости, соответствующей установившемуся периоду реактора. Такой характер изменения плотности потока определяется тем, что мгновенные нейтроны реагируют на скачкообразное изменение реактивности за очень ко­роткий промежуток времени. Однако при  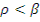дальнейшее быстрое возрастание плотности потока прекращается, так как реактор по отношению к мгновенным нейтронам подкритичен и последующее более плавное изменение обусловлено действием запаздывающих нейтронов.

Легко показать, что изменение плотности потока в первый момент времени после внесения возмущения обусловлено действием мгновенных нейтронов. Для этого выражение (12.59) продифференцируем по времени и возьмем произ­водную в момент t =0:

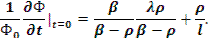
В полученном выражении левая часть представляет собой обратную величину периода. В этом легко убедиться, если продифференцировать обе части форму­лы (12.11). Тогда

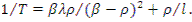
При небольших значениях ρ первый член в правой части мал по сравнению

со вторым и им можно пренебречь. В этом случае

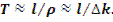
 Данный результат совпадает с формулой (12.12), когда все нейтроны только мгно­венные.

На рис. 12.4 показано изменение плот­ности потока нейтронов при скачкообраз­ном изменении реактивности для различ­ных значений р.

С увеличением реактивности возраста­ет первоначальный скачок плотности по­тока нейтронов и последующее устано­вившееся изменение потока идет быстрее. Случай ρ=0 соответствует стационарному режиму, плотность потока нейтронов не изменяется. При приближении ρ к β плот­ность потока возрастает катастрофически быстро, и реактор становится практически неуправляем.