Поскольку уравнения (12.13) и (12.25) есть линейные обыкновенные диффе­ренциальные уравнения первого порядка, возможно искать решение системы в

виде:

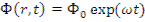                                                                                                    (12.30)

                                                                                                      (12.31)

Необходимо определить, при каких значениях параметра 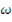, имеющего раз­мерность обратного периода, указанные решения удовлетворяют соответст­вующим уравнениям. Подставим (12.30) и (12.31) в уравнение (12.13):

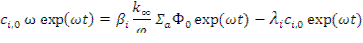
Из этого соотношения, сокращая на 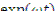, получаем

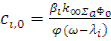                                                                                                           (12.32)

Подставив выражения (12.30) — (12.32) в уравнение (12.25), после элемен­тарных преобразований найдем

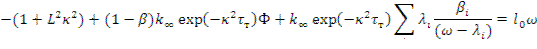
Разделив обе части уравнения на 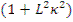, получим

                                                                                  (12.33)

где 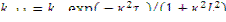 -эффективный коэффициент размножения;

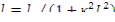- среднее время жизни теплового нейтрона в ограниченной среде с учетом утечки в тепловой области. По определению,  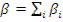и 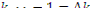. Тогда соотношение (12.33) можно записать так:

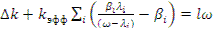                                                                                     (12.34)

Производя элементарные преобразования, получаем

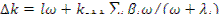                                                                                    (12.35)

Состояние реактора характеризуется еще реактивностью ρ, которая опре­деляется как отношение коэффициента избыточного размножения к эффектив­ному коэффициенту размножения [2], т.е.

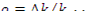
Нулевая реактивность соответствует критическому состоянию, положительная - надкритическому, отрицательная - подкритическому.

Запишем уравнение (12.35) через реактивность. Для этого разделим его члены на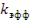

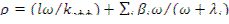                                                                                 (12.36)

Исключим из полученного уравнения 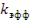  имея в виду, что 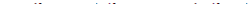. Отсюда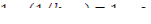

Тогда уравнение (12.36) примет следующий вид:

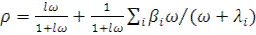                                                                           (12.37)

Полученное соотношение является алгебраическим уравнением седьмого порядка относительно 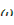 и связывает параметр  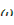с реактивностью реактора. Общий вид решения уравнения (12.37) показан на рис. 12.1.

Из графиков рис. 12.1 видно, что при учете шести групп запаздывающих нейтронов каждому значению ρ соответствует семь значений 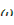. Легко видеть, что с увеличением ρ корни уравнения (12.37) асимптотически приближаются к значениям: .

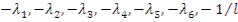На рис. 12.1 область, выделенная горизонтальными пунктирными линиями, ограничена значениями ρ=±1. Для расчета кинетики реакторов практически ин­тересна область | 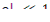. Из рисунка видно, что при любом положительном зна­чении ρ все корни, кроме cog, имеют отрицательные значения по порядку вели­чины, приближающейся к соответствующим значениям постоянных распада  ядер-предшественников, испускающих запаздывающие нейтроны. Отсюда следует, что временная зависимость плотности нейтронного потока может быть представлена в виде суммы экспонент

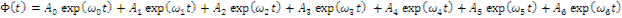 (12.38)

где 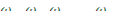 уравнения (12.37); A ₀ , А₁, А₂,.., А₆ - коэффици­енты, определяемые начальными условиями. В выражении (12.38) при положи­тельном скачке реактивности все члены, кроме первого, содержат экспоненты с отрицательными показателями. Поэтому по прошествии некоторого промежут­ка времени t (порядка 1/λ₁) в нем будет играть роль только первый член, а ос­тальные будут стремиться к нулю. В этом случае (12.38) примет вид

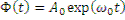                                                                                                                    (12.39)

Из определения периода реактора следует, что cuq представляет собой об­ратную величину периода реактора

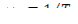                                                                                                                      (12.40)

где Т_у—установившийся период реактора [2].