Тригонометрическая форма представления синусоидально изменяющихся величин, рассмотренная нами, практически применима только для простейших электрических цепей, не содержащих большого числа контуров, источников, взаимных индуктивностей и т.п.
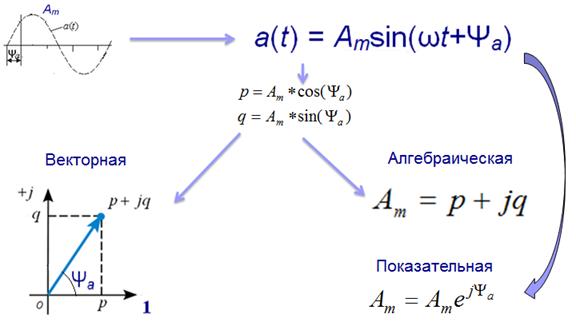
Расчет цепей переменного тока облегчается, если изображать синусоидальные величины векторами или комплексными числами. Такую возможность мы получаем благодаря тому, что между синусоидальной функцией и вращающимся вектором есть однозначное соответствие:
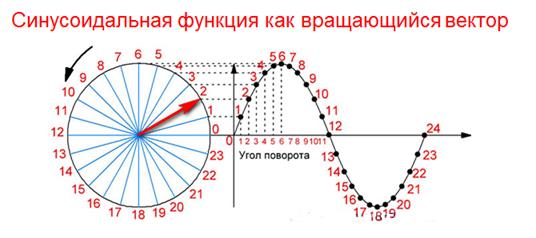
В цепи синусоидального тока все величины имеют одинаковую угловую скорость, поэтому если мы представим эти величины векторами, то окажется, что:
1. Все векторы вращаются с одинаковой угловой скоростью ω.
2. Каждый вектор характеризуется величиной (длиной) и углом поворота относительно вектора отсчета.
3. Любой вектор можно взять в качестве вектора отсчета и связать с ним систему отсчета
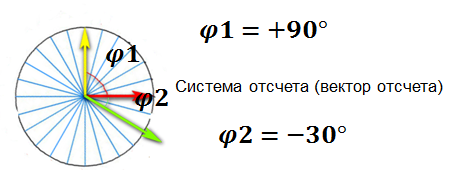
Таким образом, любая синусоидальная величина в цепи представляется вектором. Причем, размер величины равен длине вектора, а начальная фаза углу поворота.
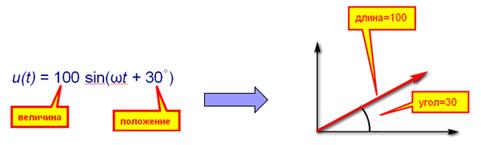
Вектор как комплексное число
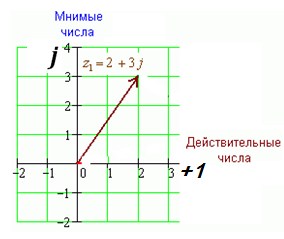
Комплексное число состоит из двух чисел – действительного и мнимого.

Комплексное число можно изобразить в виде вектора на комплексной плоскости. Таким образом устанавливается однозначная связь между комплексным числом и синусоидальной функцией
Формы представления комплексных чисел
Комплексные числа имеют несколько форм представления

Связь между формами комплексных чисел
Связь между формами комплексных чисел
Действия над комплексными числами
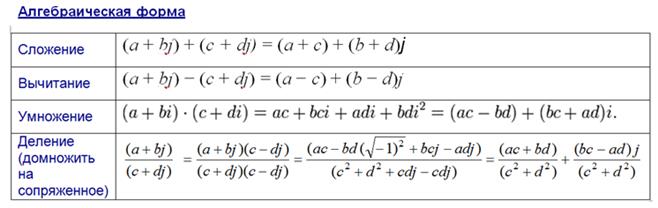
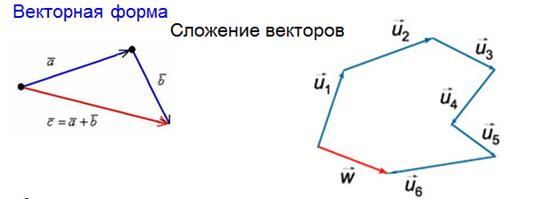
Обозначение величин
| Обозначения | Пояснения |
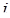 , , 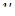 , , 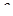
| мгновенные значения |
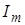 , , 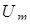 , , 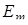
| амплитудные значения |
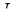 , , 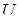 , , 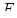
| действующие значения |
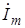 , , 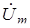 , , 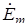
| комплексные амплитуды |
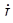 , , 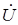 , , 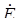
| комплексные действующие значения |
Синусоидальный ток в резисторе
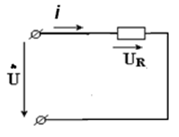
| 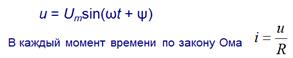 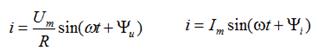
|
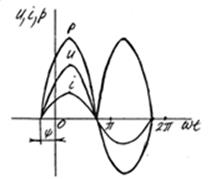
Выводы:
1. Функция тока тоже синусоидальная
2. Амплитудные значения связаны законом Ома следовательно действующие значения тоже связаны законом Ома
3. Начальная фаза тока равна начальной фазе напряжения
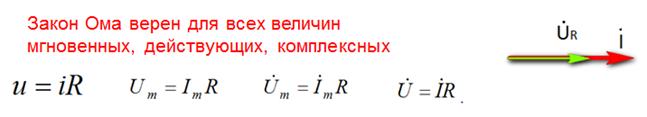
Синусоидальный ток в индуктивности
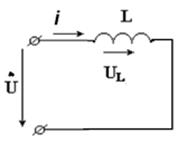
| !!! Закона Ома для мгновенных величин здесь нет |
При протекании переменного тока через индуктивность возбуждается ЭДС самоиндукции уравновешивающее соответствующее напряжение
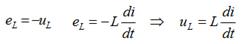
Поэтому
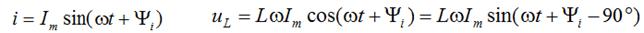
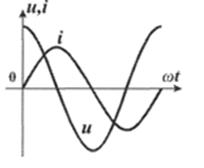
Выводы:
1. Функция тока тоже синусоидальная
2. Начальная фаза напряжения опережает ток на 90º.
3. Сопротивление индуктивности 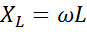
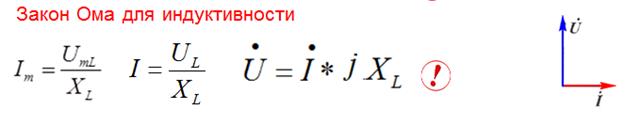
Дата: 2019-04-23, просмотров: 367.