Симметричный режим
Трехфазный приемник называют симметричным, если комплексные сопротивления всех фаз одинаковы. Если к симметричному трехфазному приемнику приложена симметричная система напряжений, то получается симметричная система токов. Режим трехфазной цепи, при котором трехфазные системы напряжений и токов симметричны, называется симметричным.
Примем, что в схеме рис. 1. 3 ZA = ZB = ZC.
Для расчета токов в фазах приемника используем закон Ома: 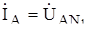 /ZA.
/ZA.
Обычно заданными являются напряжения источника питания, а не приемника. Для контура АN1NА (см. рис. 1.3) составим уравнение по второму закону Кирхгофа 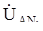 –
– 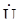 A = 0, поэтому
A = 0, поэтому 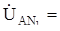
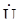 A, аналогично
A, аналогично 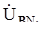 =
= 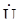 B =
B = 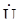 Ae–j120°,
Ae–j120°, 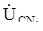 =
= 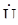 C =
C = 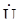 Aej120.
Aej120.
Напряжения на фазах приемника равны соответствующим напряжениям на фазах генератора, поэтому
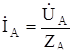 ;
; 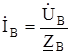 =
= 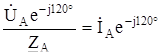 ;
; 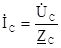 =
= 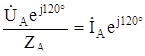 .
.
Токи в фазах приемника равны по величине и сдвинуты по фазе на 120º, поэтому расчет можно выполнить для одной фазы, обычно это фаза А приемника.
Ток в нейтральном проводе определяют, используя первый закон Кирхгофа:
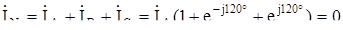 .
.
В симметричном режиме ток в нейтральном проводе равен нулю. К симметричным приемникам относятся трехфазные электродвигатели, трехфазные нагревательные устройства. При соединении этих приемников звездой нейтральный провод к нейтральной точке приемника не присоединяют.
Если в трехфазной цепи в симметричном режиме нейтральный провод отсутствует, то для расчета токов нейтральные точки генератора и приемника в схеме цепи можно соединить нейтральным проводом с сопротивлением 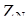 = 0. Это не изменит токи в фазах. Расчет токов выполняют для одной фазы.
= 0. Это не изменит токи в фазах. Расчет токов выполняют для одной фазы.
Аналитический расчет трехфазных цепей рекомендуется сопровождать построением векторных диаграмм.
Для трехфазных цепей чаще используют топографическую диаграмму. Она представляет собой диаграмму комплексных потенциалов точек электрической цепи. Напряжение между двумя любыми точками электрической цепи изображается вектором, соединяющим соответствующие точки диаграммы.
Точку электрической цепи, потенциал которой принят равным нулю, на топографической диаграмме помещают в начало координат. Для электрической цепи рис. 1.3. это нейтральная точка генератора N.
На рис. 1.5 приведены топографическая диаграмма напряжений и векторная диаграмма токов при симметричном режиме и индуктивном характере нагрузки (j>0) для цепи рис. 1.3.
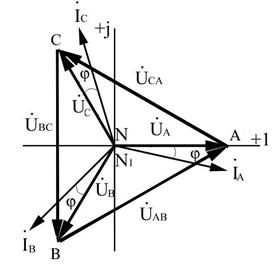
Рис. 1.5 Топографическая диаграмма напряжений и векторная диаграмма токов при симметричном режиме и индуктивном характере нагрузки (j>0) для цепи рис. 1.3
Концы векторов напряжений 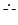 A ,
A , 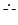 B,
B, 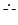 C соответствуют потенциалам точек А, В, С цепи рис. 1.3. В симметричном режиме точка N1 на диаграмме будет совпадать с точкой N, так как их потенциалы одинаковы. Направление векторов напряжений на топографической диаграмме противоположно порядку индексов напряжений, так как по правилу вычитания векторов вектор, равный разности двух векторов, соединяет концы этих векторов и направлен к уменьшаемому:
C соответствуют потенциалам точек А, В, С цепи рис. 1.3. В симметричном режиме точка N1 на диаграмме будет совпадать с точкой N, так как их потенциалы одинаковы. Направление векторов напряжений на топографической диаграмме противоположно порядку индексов напряжений, так как по правилу вычитания векторов вектор, равный разности двух векторов, соединяет концы этих векторов и направлен к уменьшаемому: 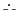 AB =
AB = 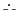 A –
A – 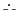 B. В приведенном выражении вектор
B. В приведенном выражении вектор 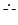 A — уменьшаемое.
A — уменьшаемое.
1.4.2. Несимметричный режим
Рассмотрим расчет токов в трехфазной цепи, схема которой представлена на рис. 1.6.
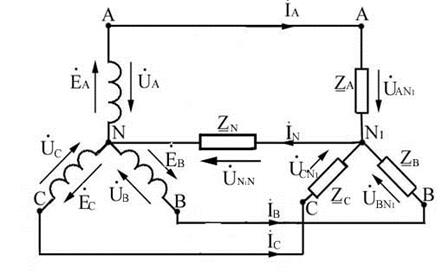
Рис. 1.6 Трехфазная несимметричная цепь при соединении генератора и приемника звездой
Примем, что ZA¹ZB¹ZC, то есть приемник несимметричный. Фазные напряжения источника питания 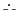 А,
А, 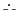 B,
B, 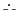 C известны.
C известны.
Так как при несимметричном режиме по нейтральному проводу пойдет ток 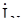 и, в общем случае, появится напряжение
и, в общем случае, появится напряжение 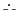 N1N между нейтральными точками приемника и генератора, то фазные напряжения и токи приемника зависят от сопротивления ZN нейтрального провода. Рассмотрим три случая:
N1N между нейтральными точками приемника и генератора, то фазные напряжения и токи приемника зависят от сопротивления ZN нейтрального провода. Рассмотрим три случая:
1. ZN = 0, то есть сопротивление нейтрального провода пренебрежимо мало.
Для контура АN1NА (см. рис. 1.6) по второму закону Кирхгофа 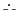 AN1 +
AN1 + 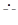 N1N -
N1N - 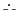 A = 0.
A = 0.
Так как 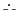 N1N = ZN
N1N = ZN 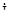 = 0, то
= 0, то 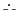 AN1 =
AN1 = 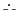 A, аналогично
A, аналогично 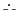 BN1 =
BN1 = 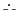 B,
B, 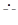 CN1 =
CN1 = 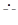 C, то есть напряжения на фазах приемника равны напряжениям на фазах генератора.
C, то есть напряжения на фазах приемника равны напряжениям на фазах генератора.
Токи в фазах приемника определяем по закону Ома:
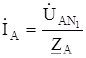 =
= 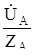 ;
; 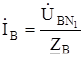 =
= 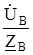 ;
; 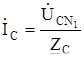 =
= 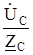 .
.
Ток в нейтральном проводе 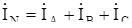 .
.
2. ZN¹0, поэтому 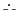 N1N = ZN
N1N = ZN 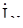 ¹0.
¹0.
По второму закону Кирхгофа напряжения на фазах приемника
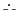 AN1 =
AN1 = 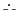 A -
A - 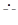 N1N ;
N1N ; 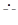 BN1 =
BN1 = 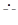 B -
B - 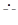 N1N;
N1N; 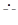 CN1 =
CN1 = 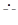 C -
C - 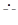 N1N.
N1N.
Напряжение между двумя узлами N1 и N схемы рис. 1.6 определим, используя метод двух узлов:
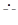 N1N =
N1N = 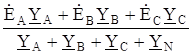 ,
,
где YA, YB, YC, YN - проводимости ветвей.
Так как для трехфазного генератора 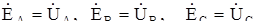
то формула для определения напряжения между нейтральными точками приемника и источника принимает вид:
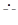 N1N =
N1N = 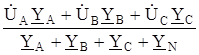 . (1.1)
. (1.1)
Токи в фазах приемника находим по закону Ома:
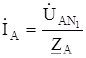 =
= 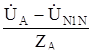 ;
; 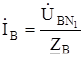 =
= 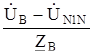 ;
; 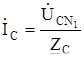 =
= 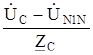 .
.
Ток в нейтральном проводе находят или по закону Ома: 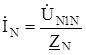 , или по первому закону Кирхгофа:
, или по первому закону Кирхгофа: 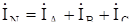 .
.
В симметричной трехфазной цепи YA = YB = YC и 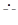 A +
A + 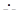 B +
B + 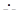 C = 0, поэтому напряжение
C = 0, поэтому напряжение 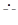 N1N по (1.1) равно нулю.
N1N по (1.1) равно нулю.
3. ZN = ¥, то есть нейтральный провод отсутствует.
Так как приемник несимметричный, то между нейтральными точками приемника и генератора будет напряжение 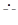 N1N. Полагая в (1.1) YN = 0, имеем
N1N. Полагая в (1.1) YN = 0, имеем
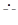 N1N =
N1N = 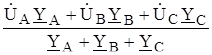 (1.2)
(1.2)
Напряжения на фазах приемника находим по второму закону Кирхгофа:
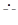 AN1 =
AN1 = 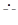 A -
A - 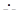 N1N ;
N1N ; 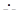 BN1 =
BN1 = 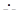 B -
B - 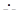 N1N;
N1N; 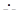 CN1 =
CN1 = 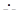 C -
C - 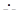 N1N.
N1N.
После этого найдем токи по закону Ома:
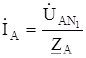 ;
; 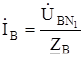 ;
; 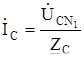 .
.
В связи с отсутствием нейтрального провода
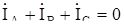 .
.
Построим топографическую диаграмму напряжений трехфазной цепи рис. 1.6.
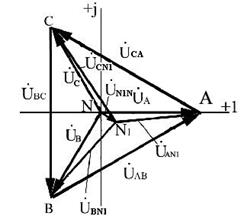
Положение точки N1 на диаграмме определяется значением вектора  N1N. Топографическая диаграмма наглядно показывает, что напряжения на фазах приемника
N1N. Топографическая диаграмма наглядно показывает, что напряжения на фазах приемника 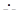 AN1,
AN1, 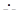 BN1,
BN1, 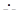 CN1 различны по величине из-за наличия напряжения
CN1 различны по величине из-за наличия напряжения  N1N. Так как все приемники рассчитаны на стандартное (номинальное) напряжение, то их эксплуатация в этом случае невозможна.
N1N. Так как все приемники рассчитаны на стандартное (номинальное) напряжение, то их эксплуатация в этом случае невозможна.
Для питания несимметричного трехфазного приемника необходимо наличие нейтрального провода с достаточно малым сопротивлением ZN, чтобы падение напряжения в нем 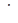 N1N = ZN
N1N = ZN 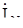 было незначительным. В этом случае фазные напряжения приемника равны фазным напряжениям генератора, которые симметричны.
было незначительным. В этом случае фазные напряжения приемника равны фазным напряжениям генератора, которые симметричны.
Несимметрию в трехфазных цепях создают однофазные приемники (электросварочные аппараты, однофазные двигатели, электрические лампы и различные бытовые приборы). При соединении таких приемников звездой обязательно используют нейтральный провод.
Если на выводах несимметричного трехфазного приемника, соединенного звездой без нейтрального провода, заданы линейные напряжения, то можно выразить фазные напряжения приемника через линейные, используя уравнение (1.2)
 AN1 =
AN1 =  A-
A-  N1N =
N1N =  A-
A- 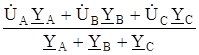 =
=
= 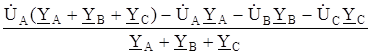 .
.
Проводим преобразования в числителе последнего выражения и учитываем, что  A-
A-  B =
B =  AB и
AB и  A-
A-  С =
С =  АC = –
АC = –  СА .
СА .
Получаем  AN1 =
AN1 = 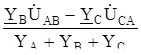 .
.
Выполняя аналогичные математические действия для нахождения напряжений на фазах В и С приемника, или используя круговую перестановку индексов АВСА и т. д., получим:
 BN1 =
BN1 = 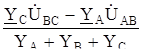 ;
;
 CN1 =
CN1 = 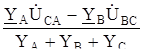 .
.
После этого находят токи, используя закон Ома.
Соединение треугольником
При соединении обмоток генератора треугольником конец первой фазы соединяют с началом второй, конец второй – с началом третьей, конец третьей – с началом первой. Аналогично поступают с фазами приемника. Общие точки каждой пары фазных обмоток генератора и общие точки каждой пары ветвей приемника соединяют линейными проводами.
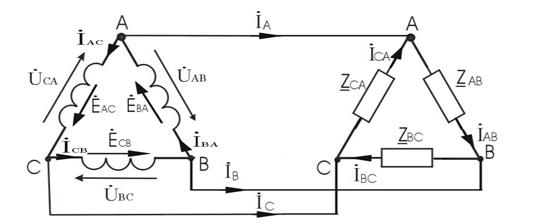
Сумма ЭДС, действующих в контуре треугольника генератора, в любой момент времени равна нулю, так как эти ЭДС равны по величине и сдвинуты по фазе на 120º. Поэтому при отсутствии нагрузки, то есть в режиме холостого хода, в обмотках генератора, соединенного треугольником, токи равны нулю.
Сопротивления фазных обмоток генератора малы и их принимают равными нулю, поэтому фазные напряжения генератора равны фазным ЭДС: 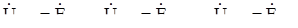 . Система фазных ЭДС генератора симметрична, поэтому напряжения
. Система фазных ЭДС генератора симметрична, поэтому напряжения  AB ,
AB ,  BC,
BC,  CA равны по величине и сдвинуты по фазе относительно друг друга на 120º.
CA равны по величине и сдвинуты по фазе относительно друг друга на 120º.
Каждая фаза генератора и каждая фаза приемника включены между двумя линейными проводами, поэтому фазные напряжения генератора, как и фазные напряжения приемника, равны линейным напряжениям:
UФ = UЛ.
Положительные направления токов в линейных проводах выбирают от источника питания к приемнику.
Положительные направления фазных токов в приемнике 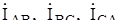 соответствуют положительным направлениям линейных напряжений
соответствуют положительным направлениям линейных напряжений  AB ,
AB ,  BC,
BC,  CA, то есть направлению АВСА.
CA, то есть направлению АВСА.
ZAB, ZBC, ZCA — сопротивления фаз приемника.
Токи в фазах приемника находят по закону Ома:
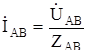 ;
; 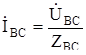 ;
; 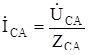 .
.
Линейные токи определяют через фазные токи, используя первый закон Кирхгофа. Для узла А приемника (рис. 1.8):  , откуда
, откуда 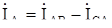 , аналогично
, аналогично 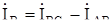 ,
, 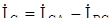 .
.
Линейные токи равны разностям соответствующих фазных токов. Сложив последние три уравнения, получим 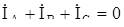 . Сумма линейных токов равна нулю.
. Сумма линейных токов равна нулю.
При симметричном режиме ZAB = ZBC = ZCA. Расчет фазного тока приемника достаточно выполнить для одной фазы, обычно это фаза АВ. 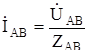 . Токи в других фазах будут равны по величине и сдвинуты по фазе на 120° к току
. Токи в других фазах будут равны по величине и сдвинуты по фазе на 120° к току 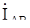 , то есть
, то есть 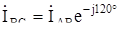 ,
, 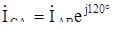 .
.
Для определения соотношения между линейными и фазными токами в симметричном режиме построим векторные диаграммы напряжений и токов (рис. 1.9).
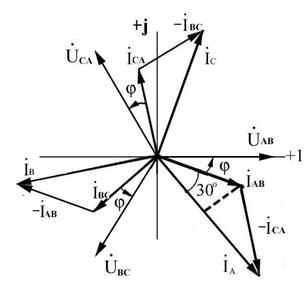
Рис. 1.9 Векторные диаграммы напряжений и токов при симметричном режиме и индуктивном характере нагрузки (j>0) для схемы рис. 1.8
При построении диаграммы напряжений принято, что начальная фаза yUAB напряжения  AB равна нулю. Характер нагрузки - индуктивный, поэтому фазные токи отстают от соответствующих фазных напряжений на угол j. Для построения векторов линейных токов использованы выражения
AB равна нулю. Характер нагрузки - индуктивный, поэтому фазные токи отстают от соответствующих фазных напряжений на угол j. Для построения векторов линейных токов использованы выражения 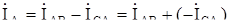 ,
, 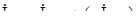 ,
, 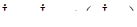 .
.
Из вершины тупого угла равнобедренного треугольника со сторонами 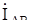 ,
, 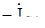 ,
, 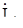 опустим перпендикуляр на вектор
опустим перпендикуляр на вектор 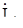 . Так как тупой угол между векторами двух фазных токов равен 120°, то острый угол равен 30°. Следовательно, из прямоугольного треугольника
. Так как тупой угол между векторами двух фазных токов равен 120°, то острый угол равен 30°. Следовательно, из прямоугольного треугольника
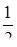 IA = IABcos30° = IAB
IA = IABcos30° = IAB 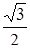 , или Iл =
, или Iл = 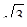 Iф.
Iф.
При симметричном режиме линейные токи больше фазных в 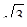 раз. Кроме того, из векторной диаграммы видно, что линейные токи отстают от соответствующих фазных токов на 30°. В комплексной форме записи
раз. Кроме того, из векторной диаграммы видно, что линейные токи отстают от соответствующих фазных токов на 30°. В комплексной форме записи 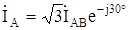 ,
, 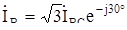 ,
, 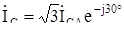 .
.
При несимметричном режиме ZAB¹ZBC¹ZCA. Фазные токи
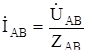 ;
; 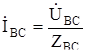 ;
; 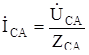
будут различны по величине и в общем случае сдвинуты относительно напряжений на разные углы. Линейные токи 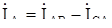 ,
, 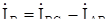 ,
, 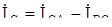 будут также различны по величине. Напряжения на фазах приемника останутся неизменными, в этом преимущество соединения фаз приемника треугольником.
будут также различны по величине. Напряжения на фазах приемника останутся неизменными, в этом преимущество соединения фаз приемника треугольником.
Трехфазный приемник соединяют треугольником, если его фазы рассчитаны на напряжение равное линейному напряжению трехфазной цепи.
Дата: 2019-04-23, просмотров: 510.