Поверхностное натяжение растворов обычно отличается от поверхностного натяжения растворителя. При растворении какого-либо вещества в растворителе возможно следующее (рис. 1):
· растворение вещества в растворителе не изменяет его поверхностного натяжения (рис. 1, прямая 2);
· повышает поверхностное натяжение растворителя (рис. 1, кривая 1);
· понижает поверхностное натяжение растворителя (рис. 1, кривая 3).
| σ0 |
| σ |
| С |
| 1 |
| 2 |
| 3 |
Рис. 1. Зависимости поверхностного натяжения от концентрации.
1 – поверхностно-инактивные вещества (ПИВ), 2 – поверхностно-неактивные вещества (ПНВ), 3 – поверхностно-активные вещества (ПАВ).
Поскольку поверхностная энергия в силу второго закона начала термодинамики стремится к минимуму, то в случае, когда растворенное вещество понижает поверхностное натяжение растворителя, концентрация этого вещества в поверхностном слое должна быть больше, чем в объеме раствора. И наоборот, когда растворенное вещество повышает поверхностное натяжение, поверхностный слой должен содержать меньше растворенного вещества, чем весь объем раствора. Таким образом, на границе раздела жидкость-газ наблюдается явление увеличения или уменьшения концентрации растворенного вещества. Самопроизвольное изменение концентрации вещества в поверхностном слое, отнесенное к единице поверхности, называется адсорбцией, обозначается через Г и выражается в моль/м2 или моль/кг. Если Г>0, адсорбцию называют положительной (растворенного вещества в поверхностном слое больше, чем в объеме), если Г<0 – отрицательной (растворенного вещества в поверхностном слое меньше, чем в объеме).
Если растворенное вещество не изменяет поверхностного натяжения, то Г=0, и вещество равномерно распределяется между поверхностным слоем и объемом раствора.
Все растворимые вещества по их способности адсорбироваться на границе раздела жидкость-газ делятся на две группы: поверхностно-активные (ПАВ) и поверхностно-инактивные вещества (ПИВ). ПАВ должны обладать меньшим поверхностным натяжением, чем растворитель, сравнительно малой растворимостью, а также способностью резко изменять свойства поверхности жидкости в результате образования тонких мономолекулярных адсорбционных слоев. К поверхностно-активным веществам относятся органические вещества, молекулы которых состоят из участков с резко различными свойствами. Одна часть молекул – полярная группа, другая – неполярная часть, состоящая из углеводородного радикала. К полярным группам относятся: -ОН, -СООН, -NH2, -SO2H и др. Полярные группы хорошо гидратируются, они и определяют сродство ПАВ к воде. Углеводородный радикал гидрофобен, т. е. понижает растворимость ПАВ в воде. При взаимодействии ПАВ с водой молекулы их погружаются в воду своими гидрофильными (полярными) группами, гидрофобная же углеводородная цепь располагается выше уровня воды. Выталкивающее действие воды на гидрофобную часть молекул ПАВ способствует накоплению их в поверхностном слое жидкости, т. е. их положительной адсорбции.
Поверхностно-инактивные вещества обладают следующими характерными особенностями: большим по сравнению с растворителем поверхностным натяжением и более высокой растворимостью. К таким веществам относятся все неорганические электролиты: кислоты, щелочи, соли, а также некоторые органические соединения, например муравьиная НСООН и аминоуксусная Н2NCH2COOH кислоты. Адсорбция поверхностно-инактивных веществ отрицательная.
Математическая зависимость между поверхностным натяжением (Н/м), концентрацией растворенного вещества С (моль/м3) и адсорбцией Г (моль/м2) была установлена Гиббсом и выражается следующей формулой:
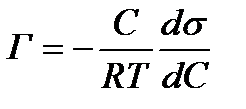 (1)
(1)
ds/dC – изменение поверхностного натяжения раствора с изменением концентрации; R – универсальная газовая постоянная; Т – температура.
Из уравнения Гиббса видно, что адсорбция положительна, если ds/dC<0, т. е. когда при повышении концентрации поверхностное натяжение понижается. Если ds/dC>0, то концентрация растворенного вещества в поверхностном слое будет меньше, чем в объеме раствора: Г<0. Когда ds/dC=0, то Г=0, т.е. адсорбции нет.
Величина ds/dC является мерой способности вещества понижать поверхностную энергию; она называется поверхностной активностью. Поверхностную активность определяют, измеряя поверхностное натяжение для разных концентраций растворов ПАВ при постоянной температуре. Строят изотерму поверхностного натяжения в виде кривой s=f(C) (рис.2, кривая 1). Используя уравнение Гиббса, получают зависимость Г от концентрации раствора при постоянной температуре, т. е. изотерму адсорбции Г=f(С) (рис. 2, кривая 2).
| С' |
| σ, Г |
| С |
| 2 |
| 1 |
| Г∞ |
| ∆σ |
| σ |
| σ0 |
Рис. 2. Зависимость поверхностного натяжения (1) и адсорбции (2) от концентрации ПАВ.
Значение ds/dC и С в уравнении (1) находят с помощью изотермы поверхностного натяжения (рис. 2, кривая 1); в приближенных расчетах ds/dC заменяют величиной Ds/DC:
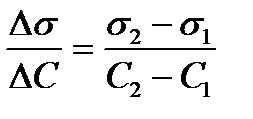 (2)
(2)
тогда:
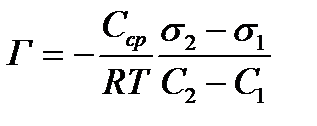 (3)
(3)
На основе графиков изотермы поверхностного натяжения и уравнения Гиббса вычисляют удельную адсорбцию Г двумя способами:
1 способ:
а) Находят значения 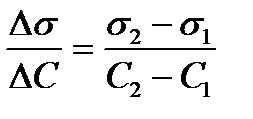 для растворов 4-5 концентраций, где
для растворов 4-5 концентраций, где
s2 – поверхностное натяжение раствора, s1 – поверхностное натяжение воды; С2 – концентрация раствора, С1=0 (т.е. все расчеты проводят относительно воды). Подставляют найденные значения в уравнение 3, в котором
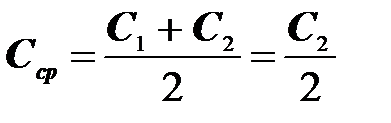 (4)
(4)
б) Находят значения Ds/DC для растворов 4-5 концентраций, как показано на рис. 3а. Для этого на начальном, наиболее крутом участке изотермы через равные интервалы концентраций берут ряд значений С1, С2, С3 и находят соответствующие значения s1, s2, s3 Рассчитывают разности Ds1=s2-s1, Ds2=s3-s2 и DС1=С2-С1, DС2=С3-С2. Подставляют их в уравнение (3).
| 1 |
| 2 |
| 3 |
| σ3 |
| σ2 |
| σ1 |
| σ |
| σ0 |
| С |
| С1 |
| С2 |
| С3 |
| а |
| 0 |
| Z |
| σ |
| σ0 |
| С |
| С |
| б |
| 0 |
Рис.3. Графические методы определения величины ds/dC: а) - первый способ;
б) - второй способ.
2 способ:
Из 5-6 произвольных точек на начальном участке изотермы поверхностного натяжения проводят касательные и горизонтальные линии до пересечения с осью ординат рис. 3б. Отрезки оси ординат, ограниченные горизонтальными линиями, касательными и обозначаемые Z, имеют следующее математическое выражение: Z= -С(ds/dC).
Величину Z измеряют в единицах поверхностного натяжения. При подстановке Z в уравнение Гиббса получают:
Г=Z/RT (5)
Определив числовые значения отрезков Z для каждой из взятых на кривой точек, находят величину Г для соответствующих этим точкам концентраций. Строят график изотермы адсорбции ПАВ (рис.2, кривая 2).
Кривая изотермы адсорбции показывает, что накопление избытка ПАВ на границе жидкость-газ стремится к некоторому пределу Г¥. Адсорбционный слой достигает насыщения. Изотерма адсорбции описывается уравнением Ленгмюра. При малой концентрации молекулы ПАВ на поверхности располагаются плашмя к поверхности (рис. 4а), что отвечает большей энергии взаимодействия с водой.
При большей концентрации в результате отталкивания углеводородные части молекул ПАВ поднимаются вверх (рис. 4б). При полном заполнении мономолекулярного слоя молекулы образуют более плотную упаковку. При этом полярные группы обращены к воде, а неполярные углеводородные радикалы располагаются вертикально к поверхности, образуя так называемый «частокол Ленгмюра» (рис. 4в).
| б |
| в |
| а |
| вода |
| газ |
Рис. 4. Расположение адсорбируемых молекул в ненасыщенном поверхностном слое (а и б) и в насыщенном (в); кружком обозначена гидрофильная часть молекул, линией гидрофобная углеводородная часть.
Каждая молекула занимает минимальную площадь на поверхности. Такое состояние адсорбционного слоя отвечает предельной адсорбции Г¥. Уравнение Ленгмюра имеет вид:
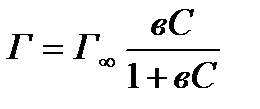 (6)
(6)
где Г¥ - предельная адсорбция, (моль/м2); в - константа равновесия, равная отношению констант скоростей процессов адсорбции и десорбции.
Для того чтобы найти константы уравнения Ленгмюра, последнее преобразуют путем деления единицы на обе его части:
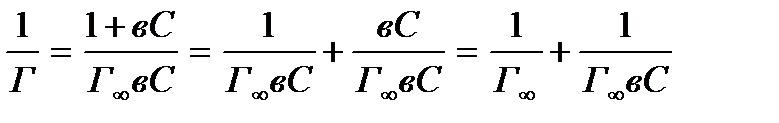
Если обозначить 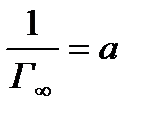 и
и 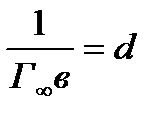 , то получаем уравнение прямой:
, то получаем уравнение прямой:
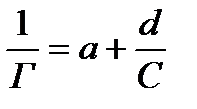 (7)
(7)
При значительном разбросе точек затрудняется выбор правильного наклона прямой. От этого будет зависеть точность определения величин а и d. В таких случаях применяют метод наименьших квадратов, который позволяет проверить линейность зависимости у=f(x), где у=1/Г, а х=1/С. Вычисленные таким путем величины а и d наиболее близки к их истинным значениям. Предельную адсорбцию находят из равенства:
Г¥=1/а (8)
Адсорбционную константу в уравнения Ленгмюра определяют графически следующим образом. На графике 1/Г=f(1/С) вверх от точки пересечения прямой с осью ординат откладывают отрезок, равный а (рис.5).
Через полученную точку А¢ проводят горизонтальную линию до пересечения с прямой зависимости 1/Г=f(1/С). Из полученной точки Д¢ опускают перпендикуляр на ось абсцисс (точка Д). Отрезок ОД представляет собой величину, равную в. По величине отрезка ОД, выраженной в единицах 1/С, находят численное значение константы:
в=ОД (9)
Размерность в обратная размерности концентрации. Численно константа в равна величине, обратной концентрации, при которой достигается 1/2 предельной адсорбции.
| 1/Г |
| 1/С |
| Д' |
| а |
| О |
| Д |
| А |
| А' |
Рис.5. График 1/Г – 1/С.
Как следствие из теории Ленгмюра принимается, что при достижении предела адсорбции на границе раздела раствор-газ образуется насыщенный монослой из молекул ПАВ, ориентированных перпендикулярно к поверхности водной фазы и плотно прижатых друг к другу. На этом основано вычисление размеров молекул ПАВ. Зная величину Г¥, находят площадь (м2) поперечного сечения полярной группы (S0) и длину d (м) молекулы ПАВ:
S0=1/(Г¥Na) (10)
d=(Г¥М)/r (11)
где Na- постоянная Авогадро, Na = 6,02×1023 моль-1; М – молекулярная масса ПАВ, кг/моль; r - плотность ПАВ, кг/м3.
Значения М и r для некоторых веществ приведены в таблице 1 (см. приложение).
Методы определения поверхностного натяжения
На практике наиболее часто используют статические или полустатические методы, позволяющие измерять равновесные значения поверхностного натяжения жидкостей. К статическим относятся методы капиллярного поднятия жидкости и висячей (лежащей) капли. Полустатическими являются методы максимального давления в капле (пузырьке), отрыва кольца или пластины и сталагмометрический метод.
Метод капиллярного поднятия
В основе метода лежит зависимость высоты поднятия жидкости h в узком капилляре от ее поверхностного натяжения. В соответствии с уравнением Лапласа избыточное давление связано с высотой h жидкости в капилляре соотношениями: Dp=2s/rм и Dp=Dρgh
rм – радиус кривизны мениска жидкости в капилляре;
Dρ – разность плотностей жидкости и газовой фазы;
g – ускорение свободного падения.
Вводя так называемую капиллярную постоянную а: а2=2s/(Dρg)=rмh
и учитывая угол смачивания θ жидкостью стенок капилляра радиусом r получаем: s=Dρgrh/(2cosθ)=a2Dρg/(2cosθ). Это соотношение известно как уравнение Жюрена. Таким образом, для определения поверхностного натяжения жидкостей этим методом экспериментально находят высоту поднятия h, радиус капилляра и угол смачивания θ. Метод капиллярного поднятия является одним из наиболее точных (относительная погрешность менее 0,01 %).
Дата: 2019-03-05, просмотров: 395.