Формула прямоугольников.
Пусть отрезок [a,b] разбит на n равных частей длины h=(b-a)/n, и в качестве точек ξk выбраны средние точки соответствующих отрезков: ξ k = a + h ( k – 1/2) ( k =1,2,…, n ). В этом случае выражение для интегральной суммы примет вид:
In = ( f (ξ1) + f (ξ2) + … + f (ξ n ))( b - a )/ n (7.1)
Если функция f(x) интегрируема на отрезке [a,b], то
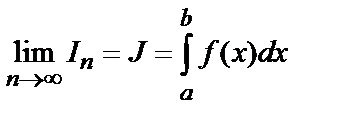(7.2)
Согласно этой формуле выражение для интеграла J можно записать в виде J=In + αn, причем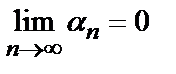 
=0. Пренебрегая величиной an , получают приближенную формулу для вычисления интеграла J, которую и называют формулой прямоугольников:
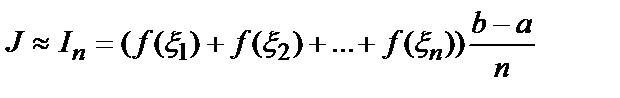(7.3)
Таким образом, интеграл J – это площадь фигуры криволинейной трапеции, а интегральная сумма, которой приближенно аппроксимируется интеграл, – площадь фигуры, составленной из прямоугольников.
| y=f(x) |
| y |
| O |
| a |
| b |
| x |
.
Вид ступенчатой фигуры показан на рисунке.
Формула трапеций.
Предположим, что отрезок [a,b] разбит на n равных частей длины h=(b-a)/n точками xk=a+kh (k=0,1,2,…,n, x0=a, xn=b). При этом, на каждом из отрезков [xk-1, xk] определим линейную функцию такую, что в граничных точках она принимает те же значения, что и функция f(x). Обобщая эту линейную функцию на n отрезков, можно выписать линейную функцию gn(x):
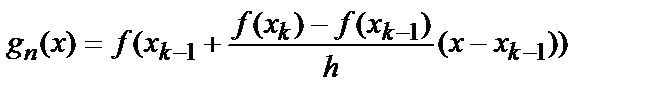) (7.4)
x Î [ xk -1 , xk ], k =1,2,…, n
Ее график представляет собой ломаную линию, начальная, конечная и угловые точки которой принадлежат также графику функции f(x).
| y=f(x) |
| y |
| O |
| a |
| b |
| x |
С увеличением n число общих точек графика растет и ломаная y=gn(x) приближается к линии y=f(x).
Интеграл равен площади фигуры, ограниченной графиком функции gn(x), осью х и вертикальными линиями x=xk-1, x=xk. В этом случае фигура является трапецией и, соответственно, полученная формула показывает площадь этой трапеции.
Переходя ко всему отрезку [a,b]:
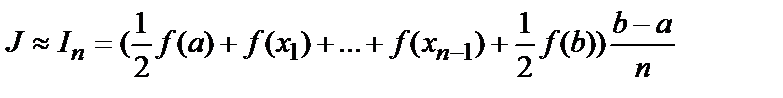(7.5)
Формула трапеций имеет второй порядок точности.
Формула Симпсона.
Идея замены графика функции f(x) на отрезке [xk-1, xk] линейной функций была использована Симпсоном, который предложил в качестве функции gn(x) использовать полином второго порядка. Тогда интеграл J будет равен:
J » In=(f(a)+4f(x1)+2f(x2)+…+2f(xn-2)+4f(xn-1)+f(b))(b-a)/(3n)
Единственное условие для возможности применения формулы Симпсона для приближенного расчета интеграла – это четное число отрезков разбиения, то есть n-четно.
| y=f(x) |
| y |
| O |
| a |
| b |
| x |
На данном рисунке количество частей разбиении исходного отрезка равно четырем – четное число.
Поскольку аппроксимирующая функция более гладкая по сравнению с другими, то порядок формулы равен 4-м.
Пример 7.1.
Найти интеграл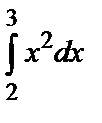 
по формулам при n=10:
а) Ньютона-Лейбница; б) прямоугольников; в) трапеций; г) Симпсона.
Решение.
Приведем графическую интерпретацию поставленной задачи.
| y=x2 |
| y |
| O |
| 1 |
| 2 |
| x |
| 2 |
Требуется найти площадь фигуры, ограниченной слева прямой х=2, справа – прямой х=3, снизу – осью абсцисс, а сверху – графиком функции y=x2.
А) Используя формулу Ньютона-Лейбница, получается:
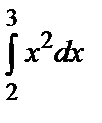=33/3 – 23/3 = 19/3 = 6,3333
Б) Для наглядности решение поставленной задачи по формуле прямоугольников приведем в виде таблицы:
| X | K | Ξk | f(ξk) |
| 2 | 0 |
|
|
| 2,1 | 1 | 2,05 | 4,2025 |
| 2,2 | 2 | 2,15 | 4,6225 |
| 2,3 | 3 | 2,25 | 5,0625 |
| 2,4 | 4 | 2,35 | 5,5225 |
| 2,5 | 5 | 2,45 | 6,0025 |
| 2,6 | 6 | 2,55 | 6,5025 |
| 2,7 | 7 | 2,65 | 7,0225 |
| 2,8 | 8 | 2,75 | 7,5625 |
| 2,9 | 9 | 2,85 | 8,1225 |
| 3 | 10 | 2,95 | 8,7025 |
| S= |
63,325
h=(3-2)/10=
0,1
I=h*S=
6,3325
Ошибка расчета составит: Er=|6,3333-6,3325|=0,0005.
В) Аналогично представим расчет по формуле трапеций в виде таблицы:
| X | K | f(x) |
| 2 | 0 | 4 |
| 2,1 | 1 | 4,41 |
| 2,2 | 2 | 4,84 |
| 2,3 | 3 | 5,29 |
| 2,4 | 4 | 5,76 |
| 2,5 | 5 | 6,25 |
| 2,6 | 6 | 6,76 |
| 2,7 | 7 | 7,29 |
| 2,8 | 8 | 7,84 |
| 2,9 | 9 | 8,41 |
| 3 | 10 | 9 |
| h=0,1 | I= |
6,335 |
Ошибка расчета составит: Er=|6,3333-6,3350|=0,0020.
Г) Таблица для формулы Симпсона:
| X | K | f(x) |
| 2 | 0 | 4 |
| 2,1 | 1 | 4,41 |
| 2,2 | 2 | 4,84 |
| 2,3 | 3 | 5,29 |
| 2,4 | 4 | 5,76 |
| 2,5 | 5 | 6,25 |
| 2,6 | 6 | 6,76 |
| 2,7 | 7 | 7,29 |
| 2,8 | 8 | 7,84 |
| 2,9 | 9 | 8,41 |
| 3 | 10 | 9 |
| h=0,1 | I= |
6,33333 |
Ошибка расчета составит: Er=|6,3333-6,3333|=0,0000.
Как видно из приведенного примера, наилучшее приближение к значению интеграла, найденного по формуле Ньютона-Лейбница, имеет формула Симпсона.
Дата: 2019-03-05, просмотров: 234.
