Пакет MathCad не имеет универсальных средств аналитического решения обыкновенных дифференциальных уравнений, однако иногда можно рассчитать аналитические решения некоторых уравнений на MathCad в соответствии с известными алгоритмами.
Один из подобных случаев – если уравнение позволяет разделять переменные, тогда можно найти аналитическое решение, путем использования оператора символьного интегрирования.
Когда аналитического решения найти нет возможности, то для численного решения обыкновенных дифференциальных уравнений используются встроенные функции для различных видов уравнений, дополнительные условия и методы решения.
Подобные функции находятся в категории Differential Equation Solving библиотеки встроенных функций. Одни из них используются в составе группы решения Given, а другие без нее – все параметры задачи передаются в виде аргументов. Использование того или иного способа зависит от конкретных целей – при использовании группы решения запись уравнений более привычна и наглядна, а отдельную функцию удобно записывать в составе других функций и программ.
Наиболее распространенной функцией для решения задачи Коши является функция
OdeSolve (x,b)
где х – независимая переменная интегрирования, а b – верхняя граница отрезка интегрирования [a,b] (естественно, что начальные условия задаются в точке а). По умолчанию для решения уравнений функция OdeSolve использует Fixed – метод Рунге-Кутты с фиксированным шагом интегрирования, но через контекстное меню его можно поменять на Adaptive –метод Рунге-Кутты с переменным шагом интегрирования, изменяемым в зависимости от скорости изменения функции решения, или Stiff – метод, адаптированный для решения жестких уравнений и систем.
Функцию OdeSolve можно использовать и для решения систем дифференциальных уравнений. К тому же функция применима и для решения дифференциального уравнения высшего порядка, которое может быть переведено в систему дифференциальных уравнений несложным преобразованием.
Решать системы дифференциальных уравнений можно и без группы решений. В MathCad для этого приспособлены несколько функций, схожих по синтаксису, но каждая из них использует свой метод. Для простых систем не играет большой роли, какой метод использовать, поскольку решение выдается моментально и с высокой точностью. Иначе для сложных систем – выбор метод является важной составляющей точного и быстрого решения.
Так, функция, являющаяся методом Рунге-Кутты с переменным шагом решения дифференциальных уравнений:
Rkadapt (y,a,b,n,D)
где y – вектор начальных условий (число);
a, b – концы отрезка интегрирования;
n – количество отрезков, на которые разбивается отрезок интегрирования; чем больше n, тем точнее найденное решение, но дольше время счета.
D=D(x,y) – векторная функция, элементы которой содержат правые части уравнений системы.
Пример 6.5.
Определить численное решение дифференциального уравнения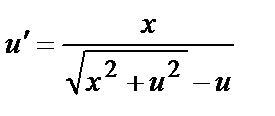 
на [0,1] и начальным условием: u(0)= - 0,5. Сравнить его с аналитическим решением.
Решение.
Вначале надо задать диапазон расчета аналитической функции y(x), вид ее определен в примере 6.1:
Чтобы применить функцию Odesolve, надо ввести расчетный блок, задаваемый Given:
Отметим, что функция OdeSolve считает функцию u численно, но не имеет возможности выдать массив данных, она лишь может выдать значение функции u в конкретных точках, при этом можно строить график функции. Покажем, что решение, получаемое функцией OdeSolve, совпадает с аналитическим решением y(x):
Пример 6.6.
Определить численное решение дифференциального уравнения методом Рунге-Кутты с автоматическим изменением шага 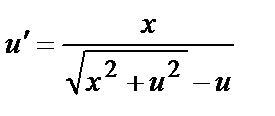на [0,1] и начальным условием: u(0)= - 0,5. Сравнить его с аналитическим решением.
Решение.
Вначале надо задать начальное значение y вектор правых частей D, при этом следует иметь в виду, что хоть в нашем случае y – одна единственная функция, но указываться она должна как массив с одним (нулевым) элементом (по умолчанию переменная ORIGIN =0):
а далее запустить функцию Rkadapt c верными аргументами:
.
В переменную G будут записаны значения массива данных:
Первый столбец – точки разбиения отрезка [0,1] на 10 частей, второй столбец – значения функции y(x)ю Нижеследующий график иллюстрирует значения рассчитанной функции:
Видно, что два последних графика совпадают друг с другом.
Пример 6.7.
Найти решение системы в MathCad:
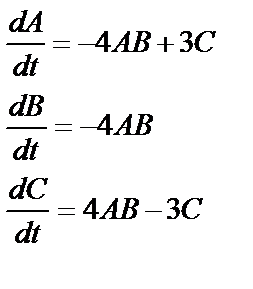
c начальными данными: A0=0,03; B0=0,04; C0=0,01 при времени от 0 до 3 мин., с шагом 0,5.
Решение.
Решение будем искать фиксированным методом Рунге-Кутты
Введем начальные данные и систему дифференциальных уравнений:
Рассчитанные данные по функциям A, B, C находятся, соответственно в столбцах 1,2,3.
Представим графики их изменения в одной системе координат:
По полученному рисунку видно, что функции, описывающие поведение первого и третьего дифференциального уравнений взаимно симметричны, то есть функции А и С. Этот результат является аналогичным результату, полученному путем решения этой системы дифференциальных уравнений в пакете MS Office Excel.
Задания для лабораторной работы №6:
Дана кинетическая схема некоторого процесса:
A + B (k1)àC
C + B (k2)àD
C (k3)àD+E
A+D (k4)à B
Начальные условия:
A(0)=0,00N; B(0)=N*2/1000; C(0)=(N+5)/100; D(0) = 0,000(N+3); E(0)=0;
k1=4,
k2=3,
k3=N/10,
k4=5.
Задание 1.
Выписать систему дифференциальных уравнений, каждое из которых представляет собой скорость изменения концентрации отдельного вещества в течение процесса.
Задание 2.
Найти решение системы методом Эйлера на отрезке по времени [0,2]:
А) с шагом 0,5;
Б) с шагом 0,25.
Задание 3.
Найти решение системы методом Рунге-Кутта 4-ого порядка на отрезке по времени [0,2] с шагом 0,5.
Определить величину погрешности и аппроксимации для функции A(t), принимая за аналитическое решение – решение, полученное методом Рунге-Кутта, а за численное решение – решение, полученное методом Эйлера.
Задание 4.
Построить в одной координатной плоскости два графика для функции А(t): решение системы ДУ методом Эйлера и методом Рунге-Кутта.
Задание 5 .
Построить в пакете MathCad таблицу, представляющую решение системы дифференциальных уравнений, описывающих химический процесс. Использовать методы rkfixed и Rkadapt.
Задание 6.
Создать графики функций А и С в одной координатной плоскости, в качестве основы принять таблицу, построенную методом rkfixed.
Задание 7.
Подготовить печатный экземпляр работы с выполненными заданиями.
Контрольные вопросы
1. Какая задача называется задачей Коши?
2. Соблюдение каких условий требуется для решения задачи Коши?
3. Опишите суть метода ломаных Эйлера.
4. Что такое точность метода?
5. Дайте определение разностной схемы метода.
6. Что такое порядок метода?
7. Что такое точность метода?
8. Дайте определение погрешности аппроксимации и погрешности решения.
9.. В чем недостаток и преимущество метода Эйлера?
10. Каков порядок метода Рунге-Кутты?
Дата: 2019-03-05, просмотров: 251.
