Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Используется для повышения точности получаемого разностного решения задачи Коши (5.1)-(5.2). Расчетные формулы разностной схемы имеют несколько иной вид. Разностное уравнение:

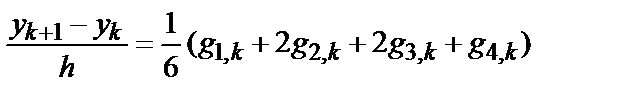           (6.14)

g_1,k = f(x_k,y_k                

g_2,k = f(x_k + h/2,y_k + h/2*g_1,k)                                                        (6.15)

g_3,k = f(x_k + h/2,y_k + h/2*g_2,k)

g_4,k = f(x_k + h,y_k + h*g_3,k)         

 

Формулы (5.15) обеспечивают точность четвертого порядка относительно h как в аппроксимации, так и в погрешности решения.

Формулу (5.14) можно переписать следующим образом:

 y_k+1 = y_k + h/6(g_1,k + 2g_2,k + 2g_3,k + g_4,k)                 (6.16)

Пример 6.3.

Определить решение дифференциального уравнения

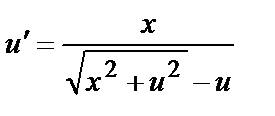 методом Рунге-Кутты 4-ого порядка точности на отрезке [0,1] с шагом h=0,5 и начальным условием: u(0)= - 0,5. Сравнить его с частным аналитическим решением уравнения. Найти погрешность решения z.

Решение.

Его общее решение имеет вид: .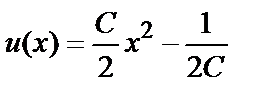

 

Определим решение методом Эйлера с шагом 0,5:

y(0)=u(0)= - 0,5

g_1,0 = f(x₀,y₀)=  0/( 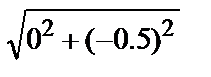 - (-0,5))=0           

g_2,0 = f(x₀ + h/2,y₀ + h/2*g_1,0) = 0,25/( 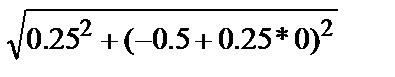-(-0.5+0.25*0))= 0,236068

g_3,0 = f(x₀ + h/2,y₀ + h/2*g_2,0)= 0,25/( 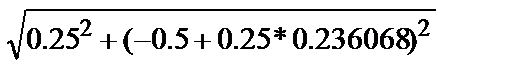 - (-0.5+0.25*0.236068))= 0,263741

g_4,0 = f(x₀ + h,y₀ + h*g_3,0)= 0,5/( 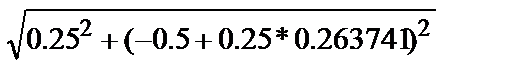 -       (-0.5+0.25*0.263741))= 0,505545

 

y(0,5) = y(0)+h( g_1,0 + 2g_2,0 +2 g_3,0 + g_4,0 )/6= -0,37457

g_1,1 = 0,500344

g_2,1 = 0,72123

g_3,1 = 0,773984

g_4,1 = 1,012499

 

y(1,0) = y(0,5)+h( g_1,1 + 2g_2,1 +2 g_3,1 + g_4,1 )/6= 0,000703

 

Расчетная таблица имеет вид:

x	g1	g2	g3	g4	y_R-K	u_analit	z	Psi
0	0	0,236	0,264	0,506	-0,5	-0,5	0	0,25
0,5	0,500	0,721	0,774	1,012	-0,375	-0,375	0,0004	0,250
1					0,001	0	0,0007

 

Аналитическое решение дает значения: u(0)=-0,5; u(0,5)= -0,375; u(1,0)= 0

Z = max|z_k| = max{0,0.00043, 0.000703}=0.000703

y = max|y_k| = max{0.25; 0.249656}=0.25

 

Соответствие метода Рунге-Кутта и аналитического решения показано на рисунке.

 

 

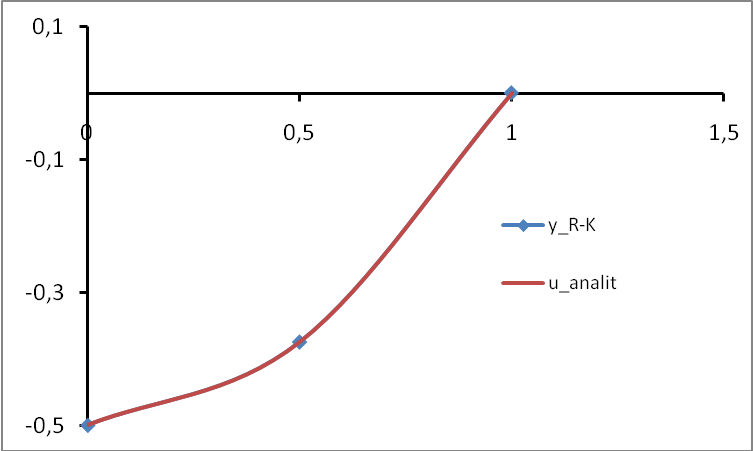
По нему видно, что аналитическое решение очень хорошо согласуется с полученными расчетными значениями, то есть расчетная кривая близка к аналитическому решению и, поэтому,  иногда за аналитическое решение принимается кривая, полученная методом Рунге-Кутты или, вообще говоря, методом высшего порядка.

Пример 6.4.

Дана кинетическая схема процесса

A + B (k1)àC

C (k2)àА

Начальные условия: A₀=0,03; B₀=0,04; C₀=0,01, k1=4, k2=3

а) выписать систему дифференциальных уравнений, каждое из которых представляет собой скорость изменения концентрации отдельного вещества в течение процесса;

б) найти решение системы методом Эйлера 1-ого порядка точности на отрезке по времени [0,3] с шагом 0,5;

в) найти решение системы методом Рунге-Кутта 4-ого порядка точности на отрезке по времени [0,3] с шагом 0,5;

г) сравнить кривые зависимости концентрации вещества А от времени, полученные двумя методами.

Решение.

а) По этой кинетической схеме можно составить систему дифференциальных уравнений:

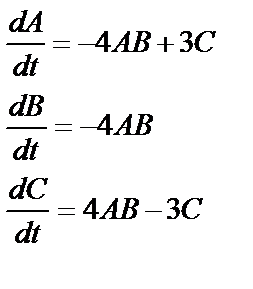
С начальными данными: A₀=0,03; B₀=0,04; C₀=0,01.

б) Все расчеты, связанные с методом Эйлера удобно вести в пакете Excel. Для этого необходимо составить расчетную таблицу. Оформим формулы, соответствующие расчету значений всех функций при времени t=0,5:

 

B3 | = B2+$A$3*(-4*$B2*$C2+3*$D2)

C3 | = C2+$A$3*(-4*$B2*$C2)

D3 | = D2+$A$3*(4*$B2*$C2-3*$D2)

Однако, такой расчет дает значение в ячейке D3 отрицательное число, что противоречит условию неотрицательности концентрации, поэтому формулу в ячейке D3 необходимо заменить на следующую:

D3 | = ЕСЛИ(D2+$A$3*(4*$B2*$C2-3*$D2)<0;0;D2+$A$3* (4*$B2* $C2 -3*$D2))

Это изменение позволит исправить ситуацию с отрицательными значениями концентраций веществ. Вообще говоря, условие неотрицательности концентраций могут быть использованы для всех веществ: А, В и С.

Тогда таблица Excel будет иметь вид:

 

 

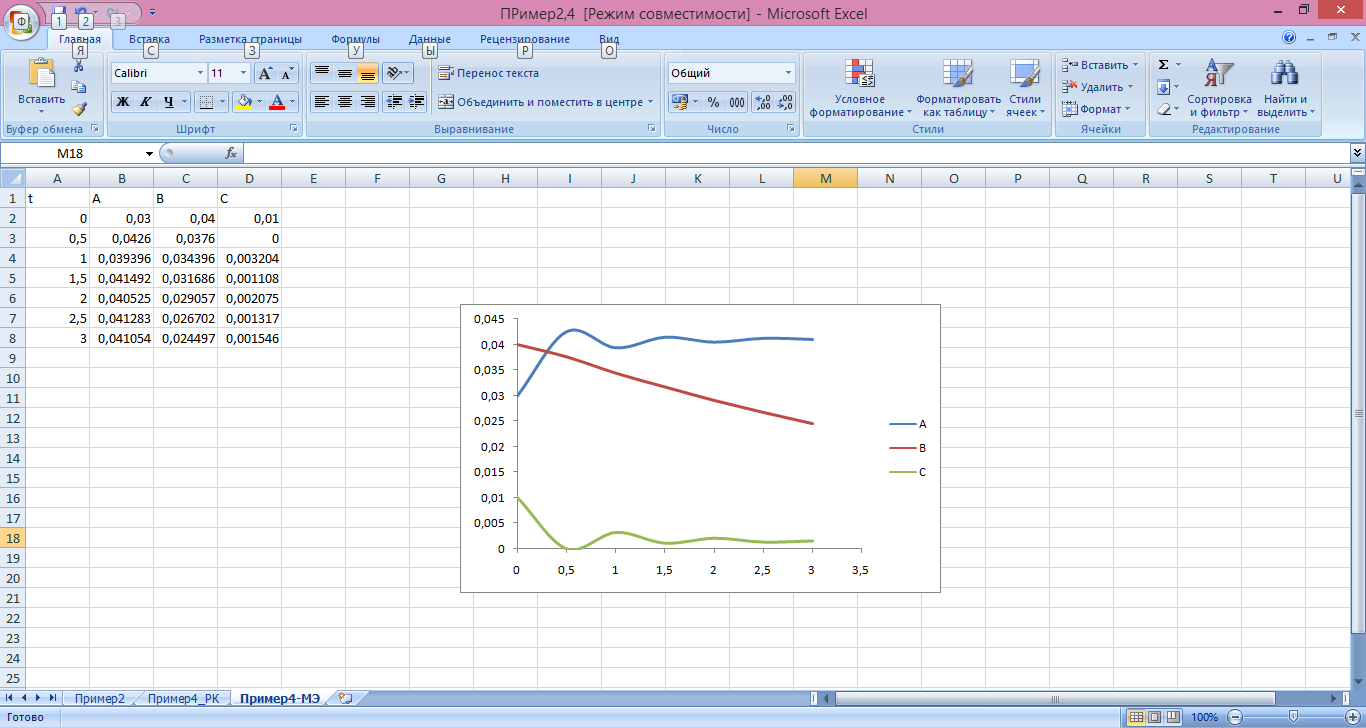
Если провести анализ полученных значений и, собственно, системы дифференциальных уравнений, приведенной в пункте а), то видно, что с увеличением времени процесса, концентрация вещества В постепенно уменьшается, об этом же и свидетельствует дифференциальное уравнение dB/dt, оно всюду отрицательно, т.е. отрицательна скорость изменения концентрации вещества, следовательно, оно уменьшается.

Вещества А и С ведут себя с точностью до наоборот, что также видно по их дифференциальным уравнениям. Для этих веществ можно выписать балансовое уравнение:

A(t)+C(t) = A(0) + C(0) = const

Если вновь посмотреть на систему дифференциальных уравнений, то можно заметить, что

dA/dt + dC/dt = 0

то есть суммарная концентрация веществ А и С постоянна и неизменна во времени. Фактически это означает, что если концентрация вещества А увеличивается, то падает концентрация вещества С, и наоборот.

Приведем графики изменения концентраций всех веществ в одной координатной плоскости:

 

 

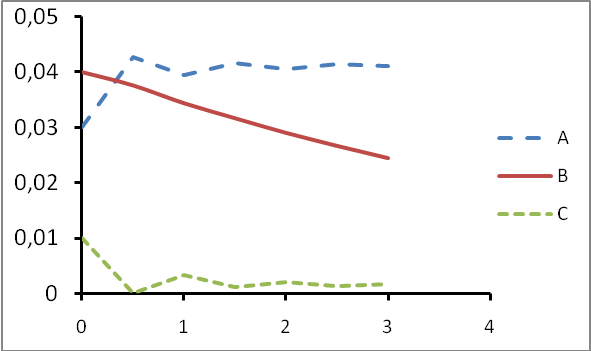
Рисунок свидетельствует обо всех выводах, полученных путем анализа системы дифференциальных уравнений, описывающих заданную кинетическую схему процесса.

Осью симметрии для кривых, характеризующих концентрации веществ А и С, является их средняя суммарная концентрация, равная:

s = (A(0) + C(0))/2 = 0,02

в) Составим расчетные таблицы, для этого внесем в ячейки B3, C3, D3, E3,F3 следующие формулы:

B3 | = -4*$F2*$F11 + 3*$F20

С3|=-4*($F2+0,5/2*B3)*($F11+0,5/2*B12)+3*($F20+0,5/2*B21)

D3|=-4*($F2+0,5/2*C3)*($F11+0,5/2*C12)+3*($F20+0,5/2*C21)

E3|=-4*($F2+0,5*D3)*($F11+0,5*D12)+3*($F20+0,5*D21)

F3|=F2+0,5/6*(B3+2*C3+2*D3+E3)

Аналогично будут выглядеть формулы в ячейках, используемых для расчета коэффициентов вещества В – это ячейки B12, C12, D12, E12 и F12:

B12 | = -4*$F2*$F11

С12|=-4*($F2+0,5/2*B3)*($F11+0,5/2*B12)

D12|=-4*($F2+0,5/2*C3)*($F11+0,5/2*C12)

E12|=-4*($F2+0,5*D3)*($F11+0,5*D12)

F12|=F11+0,5/6*(B12+2*C12+2*D12+E12)

 

Формулы, находящиеся в ячейках B21, C21, D21, E21, F21:

B21 | = 4*$F2*$F11 - 3*$F20

С21|=4*($F2+0,5/2*B3)*($F11+0,5/2*B12)-3*($F20+0,5/2*B21)

D21|=4*($F2+0,5/2*C3)*($F11+0,5/2*C12)-3*($F20+0,5/2*C21)

E21|=4*($F2+0,5*D3)*($F11+0,5*D12)-3*($F20+0,5*D21)

F21|=F20+0,5/6*(B21+2*C21+2*D21+E21)

 

Таблица в Excel будет иметь вид, показанный на нижеследующем рисунке. В ней для расчета значений каждого вещества используются свои коэффициенты g_1, g₂, g₃, g₄.

 

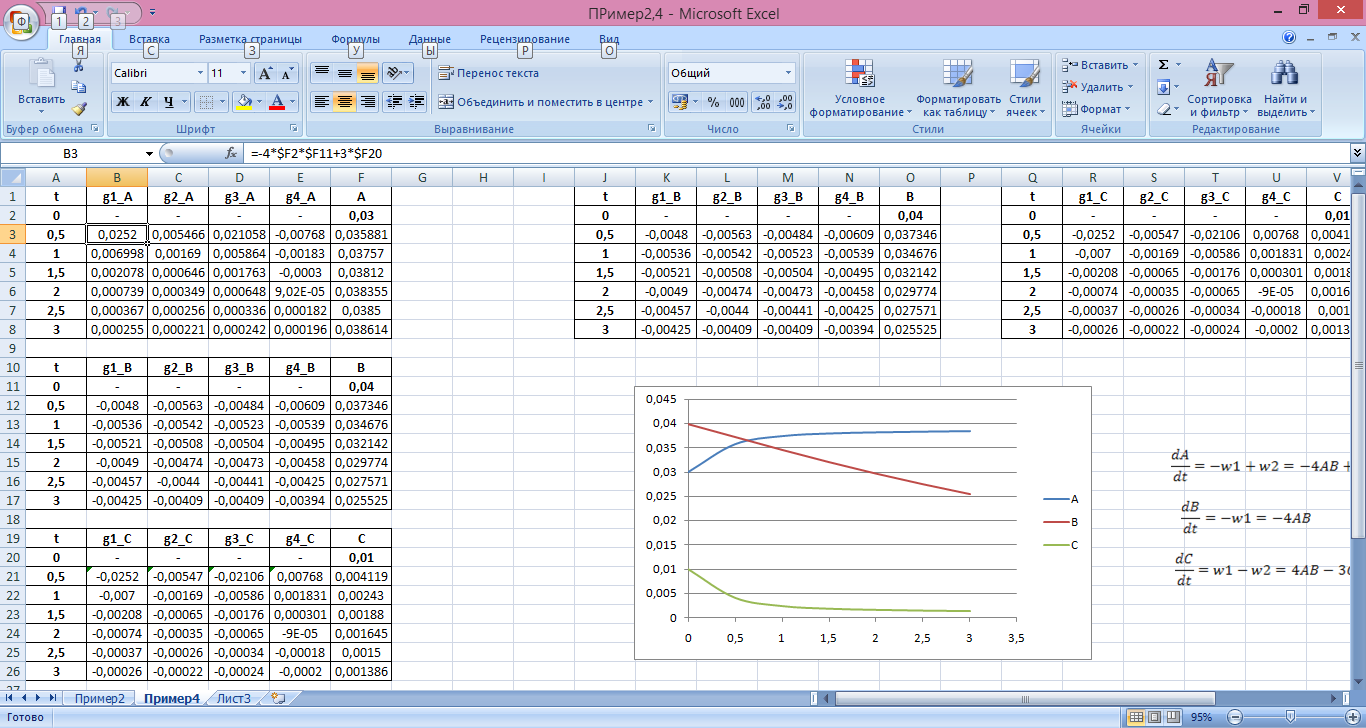
По расчетным таблицам можно построить графики изменения концентраций веществ А, В и С в одной координатной плоскости:

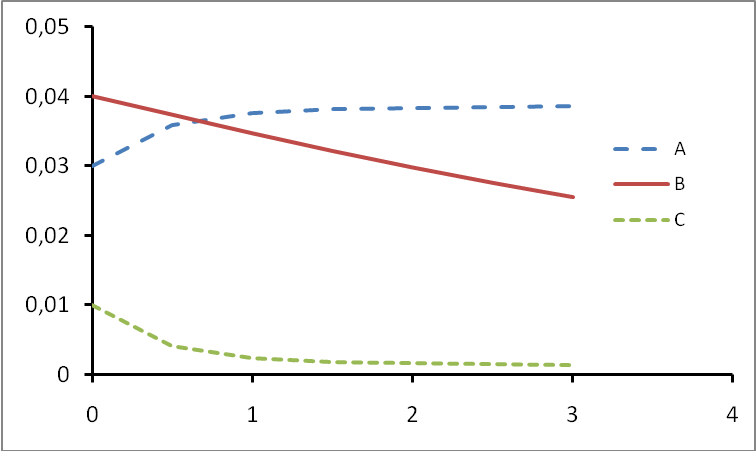
Полученный рисунок также свидетельствует  об адекватности всех полученных выводов из анализа системы дифференциальных уравнений. Явно прослеживается симметрия между графиками, характеризующими изменение концентрации веществ А и С, причем осью симметрии является число

s = (A(0) + C(0))/2 = 0,02

также как при использовании метода Эйлера.

Ниспадающий вид кривой по изменению концентрации вещества В аналогичен полученному выше методом Эйлера.

Можно сделать вывод, что полученные численными методами зависимости изменения концентраций участвующих в процессе веществ внешне схожи друг с другом, но разнятся значениями.

Так, можно отметить, что наблюдавшаяся отрицательность концентрации вещества С при использовании метода Эйлера устранена с использованием метода Рунге-Кутты. Это является следствием высокой точности последнего метода и можно утверждать, что именно такое поведение концентрации вещества С допустимо в данном случае.

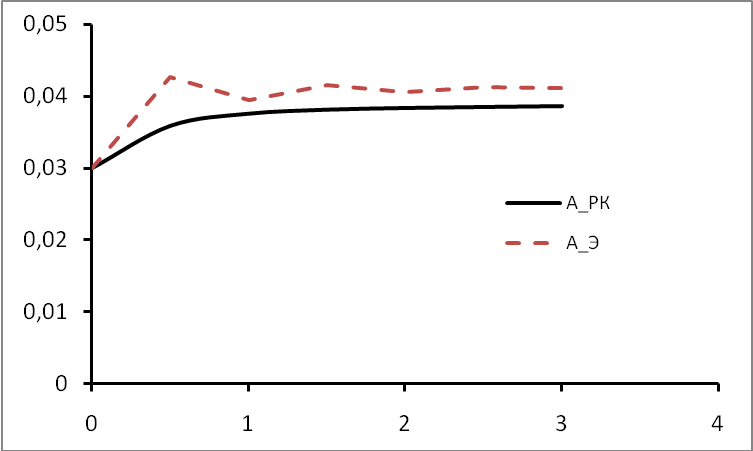
г) Сравнение методов.

Прежде чем перейти непосредственно к построению зависимости изменения концентрации вещества А, полученной двумя численными методами, построим в одной координатной плоскости решения примеров 6.1 и 6.3 совместно.

 

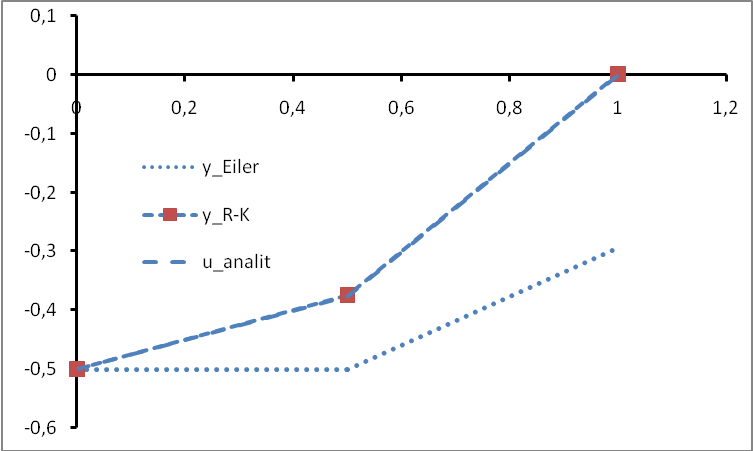
Как видно по рисунку, метод Эйлера не точно аппроксимирует аналитическое решение задачи (поскольку он первого порядка точности), а метод Рунге-Кутты очень хорошо согласуется с аналитическим решением (его точность четвертого порядка).

Этот результат является важным доказательством того, что при исследовании сложных химических процессов получение необходимых зависимостей лучше вести методом Рунге-Кутты.