Методы финансовых вычислений, базирующиеся на понятии временной стоимости денег, являются важными элементами  финансового анализа и используются в различных его разделах. Наиболее интенсивно они применяются для оценки инвестиционных проектов, в операциях на рынке ценных бумаг, в ссудозаемных операциях, в оценке бизнеса и др.

Переход к рыночной экономике  сопровождается появлением  задач эффективного вложения денежных средств. Деньги приобретают  временную ценность, которую  можно рассматривать в двух аспектах. Первый аспект связан с обесценением денежной наличности с течением времени.  Второй аспект связан с обращением капитала (денежных средств).

Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы PV с условием, что через некоторое время t будет возвращена большая сумма FV. Как известно, результативность подобной сделки может быть охарактеризована двояко: либо с помощью абсолютного показателя - прироста (FV - PV), либо путем расчета некоторого относительного показателя. Абсолютные показатели чаще всего не подходят для подобной оценки ввиду их несопоставимости в пространственно-временном аспекте. Поэтому пользуются специальным коэффициентом - ставкой. Этот показатель рассчитывается как отношение приращения исходной суммы к базовой величине, в качестве которой, очевидно, можно взять либо РV, либо FV. Таким образом, ставка рассчитывается по одной из двух формул:

В финансовых вычислениях первый показатель имеет еще названия "процентная ставка", "процент", "рост", "ставка процента", "норма прибыли", "доходность", а второй - "учетная ставка", "дисконтная ставка", "дисконт". Очевидно, что обе ставки взаимосвязаны, т.е., зная один показатель, можно рассчитать другой:

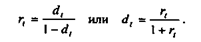
Оба показателя могут выражаться либо в долях единицы, либо в процентах. Различие в этих формулах состоит в том, какая величина берется за базу сравнения: в формуле (2.10.1) - исходная сумма, в формуле (2.10.2) - возвращаемая сумма.

Как же соотносятся между собой эти показатели? Очевидно, что r_t > d_t, а степень расхождения зависит от уровня процентных ставок, имеющих место в конкретный момент времени. Так, если r_t = 8%, d_t = 7,4%, то расхождение сравнительно невелико; если r_t = 80%, то d_t = 44,4%, т.е. ставки существенно различаются по величине.

В прогнозных расчетах (например, при оценке инвестиционных проектов), как правило, имеют дело с процентной ставкой, хотя обычно это не оговаривается. Объяснение этому может быть, например, таким. Во-первых, анализ инвестиционных проектов, основанный на формализованных алгоритмах, может выполняться лишь в относительно стабильной экономике, когда уровни процентных ставок невелики и сравнительно предсказуемы в том смысле, что их значения не могут измениться в несколько раз или на порядок, как это имело место в России в переходный период от централизованно планируемой к рыночной экономике. Если вероятна значительная вариабельность процентных ставок, должны применяться другие методы анализа и принятия решений, основанные главным образом на неформализованных критериях. При разумных значениях ставок расхождения между процентной и дисконтной ставками, как мы видели, относительно невелики, поэтому в прогнозных расчетах вполне может быть использована любая из них. Во-вторых, прогнозные расчеты не требуют какой-то повышенной точности, поскольку результатами таких расчетов являются ориентиры, а не "точные" оценки. Поэтому исходя из логики подобных расчетов, предполагающих их многовариантность, а также использование вероятностных оценок и имитационных моделей, излишняя точность не требуется.

Итак, в любой простейшей финансовой сделке всегда присутствуют три величины, две из которых заданы, а одна является искомой.

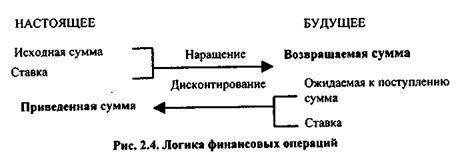
Процесс, в котором заданы исходная сумма и ставка (процентная или учетная), в финансовых вычислениях называется процессом наращения, искомая величина - наращенной суммой, а используемая в операции ставка - ставкой наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется процессом дисконтирования, искомая величина - приведенной суммой, а используемая в операции ставка - ставкой дисконтирования. В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором - о движении от будущего к настоящему (см. рис. 2.4).

Экономический смысл финансовой операции, задаваемой формулой (2.10.1), состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Поскольку из формулы (2.10.1):

FV = PV + PV ∙ r_t,

и PV ∙ r_t > 0, то видно, что время генерирует деньги.

На практике доходность является величиной непостоянной, зависящей главным образом от степени риска, ассоциируемого с данным видом бизнеса, в который сделано инвестирование капитала. Связь здесь прямо пропорциональная: чем рискованнее бизнес, тем выше значение доходности. Наименее рискованны вложения в государственные ценные бумаги или в государственный банк, однако доходность операции в этом случае относительно невысока.

Величина FV показывает как бы будущую стоимость сегодняшней величины PV при заданном уровне доходности.

Поскольку из формулы (2.10.2):

PV = FV ∙ (l - d_t)

и (1 - d_t) < 1, вновь приходим к выводу, что время генерирует деньги.

Экономический смысл дисконтирования заключается во временном упорядочении денежных потоков различных временных периодов. Одна из интерпретаций ставки, используемой для дисконтирования, такова: ставка показывает, какой ежегодный процент возврата хочет (или может) иметь инвестор на инвестируемый им капитал. В этом случае искомая величина PV показывает как бы текущую, сегодняшнюю стоимость будущей величины FV.

Пример 2.14. Предприятие получило кредит на один год в размере 5 тыс. руб. с условием возврата 10 тыс. руб. В этом случае процентная ставка равна 100%, а дисконт - 50%:

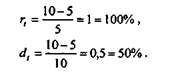
 Процентные ставки и методы их начисления

Ссудозаемные операции, составляющие основу коммерческих вычислений, имеют давнюю историю. Именно в этих операциях и проявляется прежде всего необходимость учета временной ценности денег. Несмотря на то что в основе расчетов при анализе эффективности ссудозаемных операций заложены простейшие на первый взгляд схемы начисления процентов, эти расчеты многообразны ввиду вариабельности условий финансовых контрактов в отношении частоты и способов начисления, а также вариантов предоставления и погашения ссуд.