Летняя сессия
1. Числовая последовательность. Способы задания числовой последовательности. Предел числовой последовательности. Число е.
2. Приращение аргумента и приращение функции. Понятие производной функции. Таблица производных. Сложная функция. Производная сложной функции.
3. Касательная к графику функции, ее уравнение. Геометрический смысл производной. Нормаль, угловой коэффициент нормали.
4. Производные высших порядков. Физический смысл первой и второй производной.
5. Теорема Вейерштрасса. Правило нахождения наибольшего и наименьшего значений функции.
6. Возрастающая и убывающая функции. Признак возрастания и убывания функции. Правило нахождения промежутков монотонности функции. Точки экстремума и экстремумы функции. Правило нахождения экстремумов функции.
7. Выпуклость и вогнутость кривой. Точки перегиба. Правило нахождения точек перегиба.
8. Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица неопределенных интегралов.
9. Определенный интеграл, его основные свойства. Формула Ньютона-Лейбница. Геометрический и физический смысл определенного интеграла.
10. Аксиомы стереометрии и их простейшие следствия.
11. Взаимное расположение прямых в пространстве. Пересекающиеся, параллельные, скрещивающиеся прямые. Признак скрещивающихся прямых.
12. Взаимное расположение прямой и плоскости. Параллельность прямой и плоскости.
13. Взаимное расположение двух плоскостей. Параллельность плоскостей.
14. Перпендикулярность скрещивающихся прямых. Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости. Перпендикуляр и наклонная. Два перпендикуляра к плоскости. Перпендикуляр к двум плоскостям. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Расстояние от точки до плоскости.
15. Двугранный угол и его измерение. Угол между плоскостями. Перпендикулярные плоскости. Признак перпендикулярности двух плоскостей.
16. Параллельная проекция и ее свойства. Ортогональная проекция и ее свойства. Симметрия относительно плоскости. Изображение пространственных фигур. Площадь проекции плоской фигуры.
17. Скалярные и векторные величины. Вектор. Модуль вектора. Нулевой вектор. Равные векторы. Одинаково направленные и противонаправленные векторы. Единичный вектор. Орт. Угол между двумя векторами. Ортогональные векторы. Противоположные векторы.
18. Сложение векторов. Правило треугольника, правило параллелограмма, правило многоугольника. Вычитание векторов. Умножение вектора на число.
19. Коллинеарные векторы, признак коллинеарности векторов. Разложение вектора на плоскости по двум неколлинеарным векторам. Координаты вектора. Прямоугольная система координат на плоскости.
20. Компланарные векторы, правило параллелепипеда. Разложение вектора в пространстве по трем некомпланарным векторам. Координаты вектора. Прямоугольная система координат в пространстве.
21. Действия над векторами, заданными своими координатами: сложение, вычитание векторов, умножение вектора на число. Нахождение координат вектора по координатам его начала и конца. Длина вектора. Формула расстояния между двумя точками. Скалярное произведение двух векторов. Необходимое и достаточное условие взаимной перпендикулярности двух векторов. Скалярный квадрат вектора. Скалярное умножение векторов. Нахождение угла между векторами.
22. Уравнение окружности. Уравнение сферы. Уравнение прямой. Уравнение плоскости.
23. Многогранные углы. Многогранная поверхность. Многогранник. Развертка. Сечение многогранника. Основные правила построения сечений. Сечения пирамиды и параллелепипеда.
24. Призма. Прямая и наклонная призма. Правильная призма. Перпендикулярное сечение призмы. Параллелепипед. Наклонный, прямой, прямоугольный параллелепипед. Измерения прямоугольного параллелепипеда. Куб, измерения куба. Площадь поверхности призмы. Объем призмы, прямоугольного и наклонного параллелепипеда, куба.
25. Пирамида. Правильная пирамида. Усеченная пирамида. Правильная усеченная пирамида. Апофема. Площадь поверхности пирамиды и усеченной пирамиды. Объем пирамиды и усеченной пирамиды.
26. Правильные многогранники, их свойства и развертки.
27. Цилиндр. Сечения цилиндра плоскостями. Вписанная и описанная призмы. Площадь поверхности цилиндра. Объем цилиндра.
28. Конус. Сечения конуса плоскостями. Усеченный конус. Вписанная и описанная пирамиды. Площадь поверхности конуса и усеченного конуса. Объем конуса и усеченного конуса.
29. Сфера. Шар и его части. Площадь сферы. Объем шара. Плоскость, касательная к сфере. Вписанные и описанные многогранники.
30. Понятие об объеме пространственного тела. Свойства объема. Интегральная формула объема. Равновеликие тела.
ОЦЕНОЧНОЕ СРЕДСТВО № 26
ПЕРЕЧЕНЬ ЗАДАЧ ДЛЯ ЭКЗАМЕНА
Часть 1
1. Доказать равенство:
.
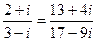2. Решить следующее логарифмическое неравенство:
.
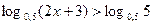3. Решить квадратное уравнение во множестве комплексных чисел:
.
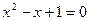4. Найти значение числового выражения:
.
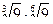5. Исследовать функцию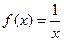 
, 
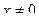, на четность и нечетность.
6. Найти значение числового выражения:
.
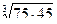7. Найти значение числового выражения:
.
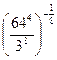8. Решить следующее логарифмическое неравенство:
.
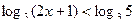9. Решить следующее логарифмическое уравнение:
.
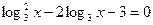10. Вычислить:
.
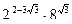11. Решить следующее показательное уравнение:
.
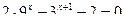12. Вычислить:
.
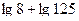13. Вычислить:
.
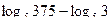14. Решить следующее показательное уравнение:
.
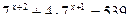15. Решить следующее показательное неравенство:
.
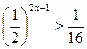16. Вычислить:
.
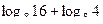17. Найти область определения функции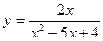 
.
18. Вычислить:
.
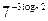19. Вычислить:
.
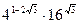20. Исследовать функцию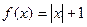 
на четность и нечетность.
21. Найти обратную функцию для функции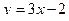 
.
22. Решить следующее показательное уравнение:
.
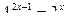23. Найти область определения функции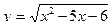 
.
24. Решить следующее показательное уравнение:
.
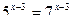25. Решить следующее показательное неравенство:
.
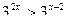26. Решить следующее логарифмическое уравнение:
.
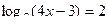27. Решить следующее логарифмическое уравнение:
.
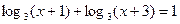28. Решить квадратное неравенство:
.
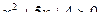29. Решить квадратное неравенство:
.
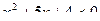30. С помощью преобразований графиков построить график функции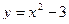 
.
31. Решить неравенство методом интервалов:
.
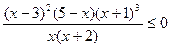32. С помощью преобразований графиков построить график функции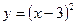 
.
33. Доказать тождество:
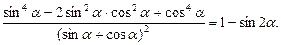
34. Решить неравенство методом интервалов:
.
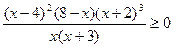35. Дано: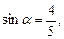 
, 
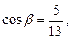
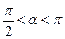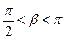. Найти: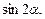 
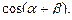
36. Найти комплексно-сопряженное число для числа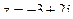 
и построить эти числа на комплексной плоскости.
37. Дано: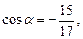 
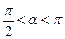. Найти: 
.
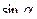38. Найти комплексно-сопряженное число для числа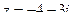 
и построить эти числа на комплексной плоскости.
39. Упростить выражение:
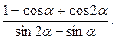
40. Перечислить свойства функции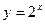 
и построить ее график.
41. Упростить выражение:
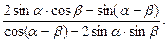
42. Перечислить свойства функции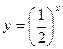 
и построить ее график.
43. Упростить выражение:
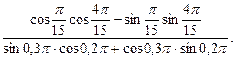
44. Перечислить свойства функции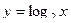 
и построить ее график.
45. Упростить выражение:
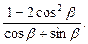
46. Перечислить свойства функции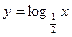 
и построить ее график.
47. Найти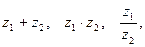 
если 
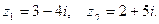
48. Упростить выражение:
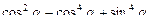
49. Найти числовое значение выражения:
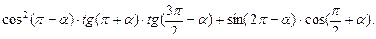
50. Решить квадратное уравнение во множестве комплексных чисел:
.
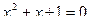51. Найти значение выражения:
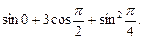
52. Представить в тригонометрической форме комплексное число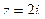 
53. Найт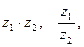и 
если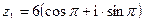 
, 
.
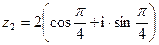54. Построить в одной системе координат графики функци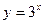й 
и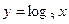 
.
55. Составить треугольник Паскаля до n=9. Найти разложение выражения (a+b)9.
56. Решить квадратное уравнение во множестве комплексных чисел:
.
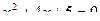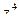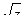57. Найти 
, 
если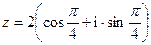 
.
58. Построить в одной системе координат графики функци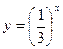й 
и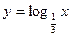 
.
59. Вычислить:
.
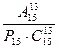60. Построить в одной системе координат графики функци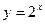й 
и .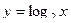
61. Найти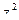 
, если 
.
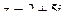62. Записать в виде бесконечной периодической дроби следующие числа:
15; 5,03;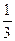 
; 
; 
.
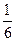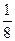63. В одной корзине находятся 5 белых и 10 черных шаров. Найти вероятность того, что вынутый наугад шар окажется черным.
64. Построить в одной системе координат графики функци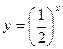й и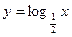 
.
65. Могут ли синус и косинус одного и того же числа быть равными соответственно:
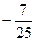и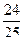 
.
66. В одной корзине находятся 5 белых и 10 черных шаров. Найти вероятность того, что вынутый наугад шар окажется черным.
67. Могут ли синус и косинус одного и того же числа быть равными соответственно:
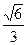и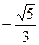 
.
68. Могут ли тангенс и котангенс одного и того же числа быть равными соответственно:
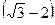и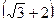 
.
69. Могут ли тангенс и котангенс одного и того же числа быть равными соответственно:
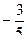и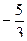 
.
70. Могут ли тангенс и котангенс одного и того же числа быть равными соответственно:
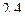и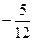 
.
Часть 2
71. n-й член числовой последовательности выражается формулой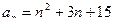 
. Найти 3-й член этой последовательности. Являются ли числа 7 и 19 членами этой последовательности, и если являются, то каковы их порядковые номера?
72. Вычислить площадь фигуры, ограниченной линиями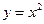 
, 
, 
, 
.
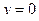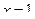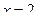73. Найти производную функции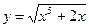 
.
74. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом 45о, если его проекция – правильный треугольник со стороной а.
75. Точка движется прямолинейно по закону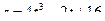 
. Вычислить скорость и ускорение точки в момент времени 
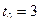с.
76. Три латунных куба с ребрами 3 см, 4 см и 5 см переплавлены в один куб. Какое ребро у этого куба?
77. Скорость движения точки изменяется по закону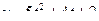 
(м/с). Найти путь s, пройденный точкой за 4 с от начала движения.
78. Если каждое ребро куба увеличить на 2 см, то его объем увеличится на 98 см3. Чему равно ребро куба?
79. Составить уравнение касательной к линии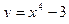 
, проходящей через точку А (1; –2).
80. Концы данного отрезка длиной 125 см отстоят от плоскости на 100 см и 56 см. Найти длину его проекции.
81. Найти производную четвертого порядка следующей функции: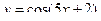 
.
82. Отрезок длиной 10 см пересекает плоскость, концы его удалены от плоскости на расстояние 5 см и 3 см. Найти длину проекции отрезка на плоскость.
83. Вычислить определенный интеграл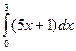 
.
84. Из некоторой точки, находящейся на расстоянии 6 см от плоскости, проведена к ней наклонная, равная 10 см. Найти ее проекцию на данную плоскость.
85. Исследовать функцию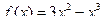 
и построить ее график.
86. Из некоторой точки проведены к данной плоскости перпендикуляр, длина которого равна а, и наклонная. Угол между ними равен 45о. Найти длину наклонной.
87. Вычислить значение производной следующих функций в точке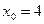 
:
а)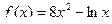 
; б)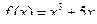 
.
88. Измерения прямоугольного параллелепипеда 15 м, 50 м и 36 м. Найти ребро равновеликого ему куба.
89. Найти производную функции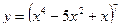 
.
90. В банку, диаметр основания которой 18 см, опущен камень, вследствие чего уровень воды в банке поднялся на 3 см. Найти объем камня.
91. Найти производную функции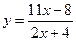 
.
92. В правильной усеченной четырехугольной пирамиде стороны верхнего и нижнего оснований равны 6 и 10 см, двугранный угол при ребре нижнего основания равен 450. Найти объем этой пирамиды.
93. Найти производную функции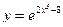 
.
94. В правильной усеченной четырехугольной пирамиде стороны верхнего и нижнего оснований равны 6 и 10 см, двугранный угол при ребре нижнего основания равен 450. Найти площадь боковой и полной поверхности.
95. Найти производную функции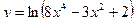 
.
96. Диаметры оснований усеченного конуса равны 6 и 10 см, его образующая наклонена к плоскости основания под углом 450. Найти объем этого конуса.
97. Найти неопределенный интеграл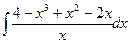 
.
98. Диаметры оснований усеченного конуса равны 6 и 10 см, его образующая наклонена к плоскости основания под углом 450. Найти площадь боковой и полной поверхности.
99. Решить тригонометрическое уравнение:
.
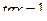100. Сфера задана уравнением: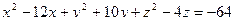 
.
Привести уравнение сферы к общему виду и найти объем шара, ограниченного этой сферой.
101. Найти производную функции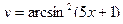 
.
102. Сфера задана уравнением: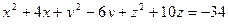 
.
Привести уравнение сферы к общему виду и найти объем шара, ограниченного этой сферой.
103. На отрезке [–10; 10] найти наибольшее и наименьшее значение функции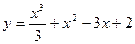 
.
104. Сфера задана уравнением: .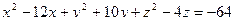
Привести уравнение сферы к общему виду и найти площадь этой сферы.
105. Найти производную функции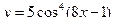 
.
106. Сфера задана уравнением: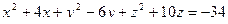 
.
Привести уравнение сферы к общему виду и найти площадь этой сферы.
107. Найти промежутки монотонности функции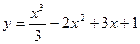 
.
108. В правильной четырехугольной призме сторона основания 4 м, боковое ребро 7 м. Найти боковую и полную поверхности призмы.
109. Вычислить определенный интеграл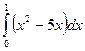 
.
110. В правильной четырехугольной пирамиде сторона основания 5 м, апофема 6 м. Найти боковую и полную поверхности пирамиды.
111. Найти неопределенный интеграл 
.
112. Осевое сечение конуса – равнобедренный треугольник с основанием 8 см и боковой стороной 5 см. Найти объем конуса.
113. Найти точки экстремума и экстремумы функции .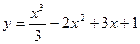
114. Площадь осевого сечения цилиндра равна 24 см2, высота цилиндра равна 6 см. Найти объем цилиндра.
115. Вычислить площадь фигуры, ограниченной линиями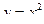 
, 
, 
, 
.
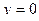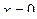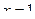116. Измерения прямоугольного параллелепипеда 2, 3 и 6 см. Найти радиус описанного около него шара.
117. Найти производную функции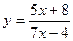 
.
118. Радиусы оснований усеченного конуса равны 4 и 1 см, образующая 5 см. Найти его высоту.
119. Найти производную функции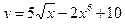 
.
120. Радиус основания конуса 3 м, высота 4 м. Найти образующую и площадь осевого сечения.
121. Решить тригонометрическое уравнение:
.
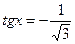122. Радиус основания цилиндра 4 м, высота 6 м. Найти диагональ осевого сечения.
123. Вычислить определенный интеграл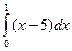 
.
124. Построить сечение куба ABCDA1 B1 C1 D1 плоскостью, проходящей через диагональ AD1 грани AA1 D1 D и середину M ребра BB1.
125. Решить тригонометрическое уравнение:
.
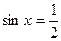126. Высота правильной четырехугольной пирамиды равна 7 м, а сторона основания равна 8 м. Найти боковое ребро и боковую поверхность.
127. Решить тригонометрическое уравнение:
.
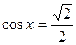128. Измерения прямоугольного параллелепипеда равны 6, 4 и 12 м. Найти диагональ параллелепипеда.
129. Вычислить определенный интеграл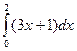 
.
130. В правильной четырехугольной призме площадь основания равна 144 см2, а высота равна 14 см. Найти диагональ этой призмы.
131. Решить тригонометрическое уравнение:
.
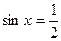132. Двугранный угол равен 45о. На одной грани дана точка на расстоянии а от другой грани. Найти расстояние от этой точки до ребра.
133. Решить тригонометрическое уравнение:
.
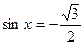134. При каких m и n векторы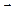 
(6; –18; n) и 
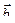(5; m; 10) коллинеарны?
135. Решить тригонометрическое уравнение:
.
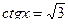136. Известно, что 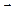(9; –2; 1) и 
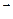(4; 3; 0).
Найти: 1)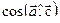 
;
2) 
;
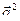3) координаты векторов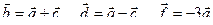 
.
137. Решить тригонометрическое уравнение:
.
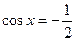138. Измерения прямоугольного параллелепипеда 2, 3 и 6 см. Найдите радиус описанного около него шара.
139. Найти неопределенный интеграл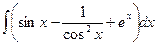 
.
140. Двугранный угол равен 30о. На одной грани дана точка на расстоянии а от другой грани. Найти расстояние от этой точки до ребра.
141. Вычислить определенный интеграл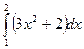 
.
142. При каких m и n векторы 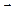(12; –6; n) и 
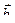(6; m; 5) коллинеарны?
143. Двугранный угол равен 60о. На одной грани дана точка на расстоянии а от другой грани. Найти расстояние от этой точки до ребра.
144. Найти производную функции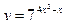 
.
145. При каких m и n векторы 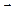(4; –10; n) и 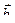(2; m; 6) коллинеарны?
Перечень рекомендуемых учебных изданий,
Дата: 2019-03-05, просмотров: 299.
