Зимняя сессия

1. Основные понятия комбинаторики. Перестановки, размещения, сочетания. Треугольник Паскаля. Бином Ньютона, свойства биноминальных коэффициентов. Формулы сокращенного умножения для старших степеней.

2. Событие. Вероятность события.

3. Натуральные, целые и рациональные числа. Десятичные дроби. Иррациональные числа. Действительные числа.

4. Комплексные числа. Действительная и мнимая часть, модуль и аргумент комплексного числа. Равные комплексные числа. Комплексно-сопряженные числа. Геометрическая интерпретация комплексных чисел. Решение квадратных уравнений при отрицательном дискриминанте.

5. Действия над комплексными числами в алгебраической форме. Степени мнимой единицы.

6. Полярные координаты точки на плоскости. Соотношения, связывающие полярные и прямоугольные координаты. Тригонометрическая форма комплексного числа. Переход от алгебраической формы записи комплексного числа к тригонометрической и обратно. Действия над комплексными числами, заданными в тригонометрической форме.

7. Числовая функция. Область определения и множество значений функции. Способы задания функции. График функции.

8. Монотонность, ограниченность, четность и нечетность, периодичность функции.

9. Преобразования графиков функций: построение графиков функций , , , .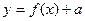

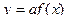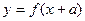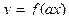10. Обратные функции. Область определения и множество значений обратной функции. График обратной функции.

11. Корень натуральной степени из числа и его свойства.

12. Степень с рациональным показателем, степень с действительным показателем и их свойства.

13. Логарифм числа. Основное логарифмическое тождество. Логарифмирование. Десятичный логарифм. Натуральный логарифм. Число е.

14. Основные свойства логарифмов. Формула перехода от одного основания логарифма к другому основанию.

15. Степенная функция, ее свойства и график.

16. Показательная функция, ее свойства и график.

17. Логарифмическая функция, ее свойства и график.

18. Радианная мера угла. Соотношения между градусной и радианной мерами угла. Синус, косинус, тангенс, котангенс острого угла и прямоугольный треугольник. Тригонометрические функции числового аргумента.

19. Знаки, периодичность, четность и нечетность тригонометрических функций. Основные тригонометрические тождества. Значения тригонометрических функций для некоторых углов.

20. Формулы приведения.

21. Формулы сложения. Формулы суммы и разности одноименных тригонометрических функций.

22. Формулы двойного и половинного аргументов.

23. Функция 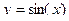, ее свойства и график.

24. Функция 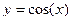, ее свойства и график.

25. Функция 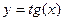, ее свойства и график.

26. Функция 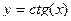, ее свойства и график.

27. Арксинус, арккосинус, арктангенс, арккотангенс числа.

28. Функция арксинус, ее свойства и график. Функция арктангенс, ее свойства и график.

29. Функция арккосинус, ее свойства и график. Функция арккотангенс, ее свойства и график.

30. Простейшие тригонометрические уравнения, их решение.

ОЦЕНОЧНОЕ СРЕДСТВО № 25