Задачи принятия решений, возникающие при управлении системами, как правило, являются многокритериальными, т.к. работа системы обычно описывается несколькими свойствами – локальными критериями.

Пусть f₁ … f_q  – критерии по которым оценивается эффективность работы системы. Каждый из q критериев зависит от вектора n  параметров. x = {x₁ … x_n} и взаимная важность критериев описывается коэффициентом относительной важности (весами) γ₁ … γ_q.

Критерии f₁ … f_q  образует вектор критериев 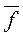, а коэффициент  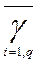- весовой вектор .

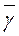Критерии f_i, например, количество и качество вырабатываемой продукции – локальные.

Каждое альтернативное решение u (конкретное значение управляющего воздействия) характеризуется присущей ему векторной оценкой (значением векторного критерия х)

.

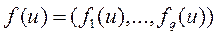Для производственной системы, состоящей из производственных подсистем (агрегаты, установки, цеха, отделы, участки и т.д.) вектор входных параметров x = {x₁ … x_n} может описывать режимные параметры, управляющие воздействием, вектор выходных параметров (в том числе и критерий оценки) – как результаты функционирования систем.

Каждый локальный критерий связан со значениями входных воздействий. Эти зависимости может описывать система моделей объекта.

Задачу принятия решений можно сформулировать следующим образом. Найти вектор управляющих воздействий 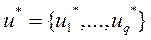, обеспечивающий такие значения локальных критериев, которые удовлетворяют лицо, принимающее решение.

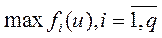
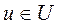
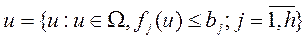
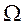 - исходное множество управлений

Принятие решений для вывода наилучшей из альтернатив

Процесс принятия решений может возникать в одной из следующих ситуаций:

1. Принятие решений в условиях определенности, когда данные известны точно

2. Принятие решений в условиях риска, когда данные можно описать с помощью вероятностных распределений

3. Принятие решений в условиях неопределенности, когда данным нельзя приписать весовые коэффициенты, которые представляли бы степень их значимости в процессе принятия решений.

Метод анализа иерархий

Этот метод является одним из подходов к принятию решений в условиях определенности, когда для идей, чувств, эмоций определяются некоторые количественные показатели, обеспечивающие числовую шкалу предпочтений для возможных альтернативных решений.

В случае, когда альтернативные решения можно связать между собой точными линейными функциями применяются методы линейного программирования.

Общая структура метода анализа иерархий может включать несколько иерархических уровней со своими критериями.

Если есть n критериев на заданном уровне иерархии, то составляется матрица А размерности n x n, называемая матрицей парных сравнений, отражающая суждение лица, принимающего решение, относительно важности разных критериев. Парное сравнение выполняется таким образом, что критерий в i-ой строке ( 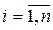) оценивается относительно каждого из критериев, представленных n столбцами.

Обозначим через a_ij элемент матрицы А, находящийся на пересечении i-ой строки и j-го столбца. В методе анализа иерархий для определения относительных весовых коэффициентов, оценивающих альтернативные решения, используются целые числа от 1 до 9. При этом 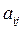 = 1 означает, что i-й и j-й критерии равнозначны, 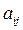= 5 отражает мнение, что i-й критерий значительно важнее j-го, а 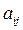= 9 означает, что i-й критерий чрезвычайно важнее j-го.

Согласованность таких обозначений обуславливается следующим условием: если 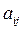 = k, то .

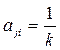Кроме этого, все диагональные элементы 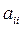 матрицы А должны быть равны 1, поскольку выражают оценку критерия относительно самого себя.

Например, матрица сравнения А имеет вид:

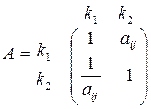                                              (1)

Относительные веса критериев k1 и k2 определяются в виде средних значений элементов соответствующих строк нормализованной матрицы А, полученной путем деления элементов каждого столбца матрицы А на сумму элементов этого же столбца, т.е. получаем нормализованную матрицу N. Для матрицы сравнения А из (1) получим матрицу N:

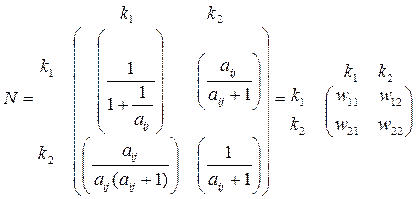          (2)

Средние значения элементов строк матрицы N определяют следующим образом:

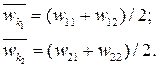
Столбцы матрицы N будут одинаковы, когда лицо принимающее решение, проявляет идеальную согласованность в определении элементов матрицы А.

Согласованность означает, что решение будет согласованно с определениями парных сравнений критериев или альтернатив.

С математической точки зрения согласованность матрицы А означает, что

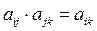для всех i, j и k.

Свойство согласованности требует линейной зависимости столбцов (и строк) матрицы А. В частности, столбцы любой матрицы сравнений размерностью 2х2 являются зависимыми и, следовательно, такая матрица всегда будет согласована.

Не все матрицы сравнений (для нескольких альтернативных решений) являются согласованными, поскольку строятся на основе субъективизма ЛПР.

Для определения «допустимости» уровня согласованности определяется соответствующая количественная мера для матрицы А.

Выше было сказано, что идеально согласованная матрица сравнений порождает нормализованную матрицу N, у которой все столбцы одинаковые.

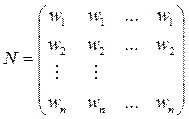                                  (3)

Для определения матрицы А из N необходимо разделить элементы i-го столбца матрицы N на w_i (обратная процедура)

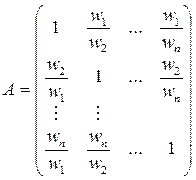                                  (4)

Согласованность матрицы определяется равенством всех ее столбцов:

            (5)

В векторном виде матрица А будет согласованной тогда и только тогда когда

A·w = n·w, где w – вектор-столбец

относительных весов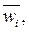

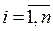
Если матрица А не будет согласованной, то относительный вес 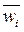 аппроксимируется средним значением n элементов i-ой строки нормализованной матрицы N.

Обозначив через 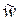 вычисленную оценку (среднее значение) можно показать, что

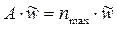                                         (6)

где .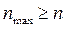

В этом случае, чем ближе n_max к n, тем более согласованной является матрица сравнения А.

Вычисляется коэффициент согласованности

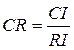,                                            (7)

где 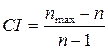 – коэффициент согласованности матрицы А           (8)

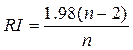 – стохастический коэффициент согласованности (9)

1.98 – критический коэффициент значимости.

Стохастический коэффициент согласованности RI определяется эмпирическим путем как среднее значение коэффициента CI для большой выборки генерированных случайным образом матриц сравнения А.

Если CR ≤ 0.1, то уровень несогласованности является приемлемым. Иначе, ЛПР рекомендуется проверить элементы парного сравнения 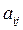 матрицы А для получения более согласованной матрицы.

n_max вычисляется из матричного уравнения.

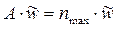, так как

,

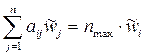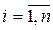
Так как 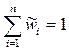, то

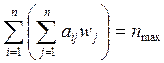
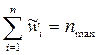,                  (10)

т.е. n_max можно определить путем вычисления вектор-столбца 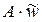 с последующим суммированием его элементов.