Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Традиционным представлением о математической модели является ее восприятие как инструмента для прогнозирования последствий альтер­нативных действий с целью выбора наиболее предпочтительного. Однако значительно важнее то, что моделирование — это метод, повышающий эффективность суждений и решений. Математические модели использу­ются для формализации целей, присущих большинству экономических систем, и имеющихся ограничений, налагаемых действующими экономи­ческими законами.

Однако имеется большое количество проблем, не поддающихся аде­кватному моделированию, например: защита окружающей среды от за­грязнений, предотвращение преступности, управление развитием и ростом городов, и т. п., - они характеризуются неясностью и противоречивостью целей, альтернатив развития, диктуемых нестабильными политическими и социальными факторами.

Математические модели многофункциональны, их основные функ­ции характеризуют широту области их применения:

1. модели являются важным средством осмысления действительности (графические, масштабные, сетевые модели);

2. модели выступают своеобразным средством общения, поскольку в сжатой, точной форме позволяют организовать диалог;

3. модели выполняют функцию обучения и тренажа (обучающие программы, имитационные игры на ЭВМ, использующие принципиально отличные от реальных стимулы и мотивы принятия решений);

4. модели широко используются как инструмент прогнозирования и планирования, позволяя рассмотреть значительное число альтернатив и оценить возможные последствия от принятия того или иного решения;

4. моделирование является основным методом оптимизации управленческих решений, отображая или воспроизводя условия развития исследуемого процесса;

5. применение моделей как средства построения экспериментов позволяет осуществлять управление процессом экспериментирования с большей простотой и меньшими затратами, чем если бы эксперимент проводился с реальной системой, получая, зачастую, больше полезной информации о поведении системы в условиях широкого спектра изменяющихся факторов внешней среды.

Экономико-математическая модель — это совокупность матема­тических выражений, описывающих экономические объекты, процессы и явления, исследование которых позволяет получить необходимую инфор­мацию для реализации целей управления, моделируемой системой.

Экономико-математическая модель, как правило, включает три ос­новные составные части:

1)целевую функцию, или функционал модели — математическое выражение цели;

2)систему функциональных ограничений, определяющих пределы изменения исследуемых характеристик объектов, процессов или явлений;

3)систему параметров модели, фиксирующих условия проведения модельного эксперимента (система норм, нормативов, временные параметры реального времени и (или) системного времени, начальные условия и т. п.).

В общем виде статическая экономико-математическая модель сис­темы может быть записана в виде:

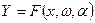              (2.7)

где х — экзогенные переменные, или управления, управляемые перемен­ные, факторы, входы;

ω - неуправляемые переменные, или возмущения;

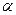 - параметры системы; любые действительные числа;

Y— эндогенные, или зависимые переменные, отклики;

F — определяет вид функциональной зависимости, играет роль оператора преобразования.

Пусть, например, F — линейный оператор. Тогда по определению линейного оператора при х = х₁ + х₂

,

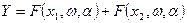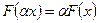
где х₁, х₂- любые функции,

 - действительное число.

Линейным оператором является оператор тождественного преобра­зования, дифференцирования, интегрирования, правого сдвига, левого сдвига, суммирования, скалярный оператор.

При изучении экономической системы в движении уравнение модели примет вид:

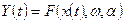(2.8)

При этом часто используют две концепции построения динамических моделей: без учета лагов, или запаздываний между входами и выходами — так называемые динамические безынерционные модели; и с учетом лагов — инерционные динамические модели. Безынерционные иначе называют кинематическими. Следует подчеркнуть, что кинематическая модель от­личается от динамической тем, что переходные процессы в системе, обу­словленные ее инерционными и демпфирующими свойствами, не учиты­ваются. В информативном отношении они менее содержательны, чем ди­намические. В английском языке для описания таких систем служат тер­мины «dinamic» и «dinamical».

Классификация моделей

Модели классифицируются по временному признаку и по математическому аппарату. По временному признаку математические модели классифицируют на:

1) статические;

2) динамические.

Статические модели предназначены для описания стационарных процессов, т.е. процессов, которые в явном виде не зависят от времени. Условно-статические модели – статические на отрезках времени.

Динамические модели служат для описания нестационарных процессов, т.е. процессов, которые имеют явную зависимость от времени.

Статические модели бывают:

1) аналитические (уравнение зависимости в явном виде);

2) статические статистические (модели дисперсионного, корреляционного, регрессионного анализа);

3) феноменологические (внешний вид регрессионных моделей, однако коэффициенты проставляет сам специалист).

Динамические модели бывают:

1) детерминированные (аналитические);

2) вероятностные (стохастические).

Динамические детерминированные модели имеют вид обыкновенных дифференциальных уравнений первого порядка.

Стохастические модели имеют вид обыкновенных дифференциальных уравнений первого порядка с Винеровской добавкой:

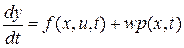
По математическому аппарату математические модели делятся на:

1) детерминированные (аналитические);

2) вероятностные (статистические).

Детерминированные модели могут описываться с помощью аппарата математического анализа конструктивных теорий функций.

Вероятностные модели – могут описываться с помощью теории вероятности, математической статистики и теории случайных процессов.

Статические статистические модели – описывают стационарные процессы методиками регрессионного и дисперсионного анализа, причем регрессионные полиномы имеют вид не более второго порядка.

Статические детерминированные модели – описывают стационарные процессы с помощью теории множеств или аппарата алгебры.

Динамические статистические модели описывают нестационарные процессы с помощью математического аппарата теории случайных процессов и описываются в виде стохастических дифференциальных уравнений.

Динамические детерминированные модели описывают нестационарные процессы в объектах с помощью математического аппарата дифференциальных и интегральных уравнений.

Уравнения в частных производных служат для моделирования в целях исследования объекта. Но для разработки систем оптимального управления объектами такие модели не подходят из-за медленной сходимости метода сеток (метод решения дифференциальных уравнений в частных производных).

При классификации экономико-математических моделей учитыва­ются различные признаки, каждый служит определенной цели. Некоторые типовые группы моделей, которые могут быть положены в основу системы классификации:

• статические и динамические;

• детерминированные и стохастические;

• дискретные и непрерывные;

• линейные и нелинейные;

• балансовые модели;

• имитационные модели;

• модели математического программирования;

• модели, основанные на теории графов;

• модели, основанные на теории вероятностей и математической статистике.

При моделировании сложной системы исследователь обычно иссле­дует совокупность нескольких моделей из числа разновидностей, упомянутых выше. Любая система может быть представлена различными способа­ми, отличающимися по сложности и в деталях. По мере того, как исследо­ватель глубже анализирует и познает проблему, простые модели сменяют­ся все более сложными.

 

Методика моделирования

Основой успешной методики моделирования является многоэтапный процесс отработки модели. Обычно начинают с более простой модели, по­степенно совершенствуя ее, добиваясь, чтобы она отражала моделируемую систему более точно. До тех пор, пока модель поддается математическому описанию, исследователь может получать все новые ее модификации, де­тализируя и конкретизируя исходные предпосылки. Когда же модель ста­новится неуправляемой, проектировщик прибегает к ее упрощению и ис­пользует более общие абстракции. Процесс моделирования, таким обра­зом, носит эволюционный характер и осуществляется в соответствии со следующими этапами.

Этапы моделирования:       

1.анализ проблемы и определение общей задачи исследования;

2.декомпозиция общей задачи на ряд более простых подзадач, образующих взаимосвязанный комплекс;

3.определение четко сформулированных целей и их упорядочение;

4.поиск аналогий или принятие решений о способе построения подмоделей;

5.выбор системы экзогенных и эндогенных переменных, необходимых параметров;

6.запись очевидных соотношений между ними;

7.анализ полученной модели и начало эволюционного конструирования: расширение или упрощение модели.

Упростить модель можно, выполнив одну из перечисленных ниже операций:

• превращение переменных величин в константы;

• превращение вероятностных факторов в детерминированные;

• исключение некоторых переменных или их объединение;

• использование предположений о линейном характере зависимостей между переменными;

• введение жестких исходных предпосылок и ограничений;

• уменьшение количества степеней свободы путем наложения более жестких граничных условий.

Расширение модели предполагает обратное.

Заметим, что не существует надежных и эффективных рецептов отно­сительно того, как следует осуществлять процесс моделирования, поэтому процесс разработки модели зачастую носит эвристический характер, что да­ет возможность исследователю проявить свои творческие способности.

Творческий характер процесса моделирования определяет разнооб­разие критериев оценки качества модели. С точки зрения разработчика «хорошей» моделью является нетривиальная, мощная и изящная модель. Нетривиальная модель позволяет проникнуть в сущность поведения системы и вскрыть детали, не очевидные при непосредственном наблюдении. Мощная позволяет получить множество таких нетривиальных выводов. Изящная имеет достаточно простую структуру и реализуемость. С точки зрения пользователей, которые проявляют больше прагматизма при оценке модели, «хорошая» модель — это модель релевантная, точная, результа­тивная, экономичная. Модель является релевантной (от англ. relevance — уместность), если она соответствует поставленной перед ней цели; точной, если ее результаты достоверны; результативной, если полученные ре­зультаты дают продуктивные выводы; и экономичной, если эффект от ис­пользования полученных результатов превосходят затраты на ее разработ­ку и реализацию.

В любом случае исследователь должен обосновывать необходимость использования конкретно применяемой модели.

Обоснование модели предполагает выполнение следующих проце­дур:

1. верификация, проведение которой убеждает в том, что модель ведет себя так, как было задумано;

2. оценка адекватности — проверка соответствия между поведением модели и поведением реальной системы;

3. проблемный анализ — формулировка значимых выводов на основе результатов, полученных в ходе моделирования.

Как показывает опыт, наибольшая обоснованность модели дости­ гается:

• использованием здравого смысла и логики;

• максимальным использованием эмпирических данных;

• проверкой правильности исходных предположений и корректности преобразований от входа к выходу;

• применением на стадии доводки модели контрольных испытаний модели, подтверждающих работоспособность модели;

• сравнением соответствия входов и выходов модели и реальной системы (если они доступны) с использованием статистических методов и испытаний типа теста Тьюринга;

• проведением, когда это целесообразно, натурных или полевых испытаний модели или ее подмоделей;

• проведением анализа чувствительности модели по отношению к изменяющимся внешним условиям;

• сравнением результатов модельных прогнозов с результатами функционирования реальной системы, которая подвергалась моделированию.

ПРЕЗЕНТАЦИЯ 2