Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Вероятность достижения цели действия сил за заданное число шагов (или за заданное время) опреде­ляется как вероятность того, что система за п шагов перейдет в некоторые состояния.

Обозначим через [А_r] множество состояний системы, переход в которые означает достижение цели действий. В частном случае это может быть и одно состояние. Показатель эффективности Э(п) будет равен

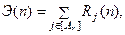                                                                            (24)

где символом j Î [А _r] обозначается суммирование по всем со­стояниям из множества [А_r], а R_j(n) – вероятность перехода системы в состояние А_j через n шагов, если до первого шага были известны вероятности нахождения системы в каждом из «начальных» состояний p_j⁽⁰⁾.

Так, для условий примера 1 будем иметь

Э(п) = R₄ (п).

Допустим, что в условиях примера 2 дополнительным пока­зателем эффективности является вероятность поражения всех ко­раблей охранения. Этот показатель будет равен

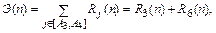
Вероятность того, что цель действия сил будет достигнута именно на п- м шаге определим для случая, когда множество состояний [А _r], означающих достижение цели действий, является поглощающим. При этом функция Э(п)  [см. формулу (24)] является неубывающей функцией аргумента п. Искомая вероятность

                                         Э'(п) = Э(п) – Э(п – 1).                                 (25)

Так, в примере 5 вероятность получения на КП сообщения именно при п-й его передаче с подводной лодки будет равна

Э'(п) = W(п) – W(п – 1).

Математическое ожидание числа шагов, необ­ходимых для достижения цели действий определим для случая дискретной цепи с невосстанавливаемым ущербом, ко­гда матрица перехода имеет одно поглощающее состояние или одну группу поглощающих состояний [А _r].

Поставим следующую задачу. Система начинает функциониро­вать из состояния А_i. Функционирование системы прекращается или при первом достижении системой множества поглощающих состояний [А _r], или же, если необходимые состояния не достигну­ты, после осуществления заданного числа шагов процесса N.

Необходимо определить математическое ожидание 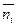(N) числа шагов до прекращения функционирования системы.

Обозначим через W_i (п) вероятность того, что искомые состоя­ния будут достигнуты после п шагов процесса при условии, что процесс начат из состояния А_i :

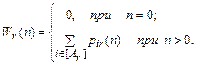
Вероятность того, что система прекратит функционирование именно на п-м шаге процесса (при п = 1, 2, ... , N – 1) равна вероятности достижения системой состояний [А_r] именно на п-м шаге [см. формулу (25)], т. е.

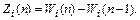
Система осуществит все N шагов в том случае, если за преды­дущие (N – 1) шагов необходимые состояния не будут достигнуты. Вероятность этого события

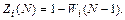
Поэтому искомое математическое ожидание числа шагов системы будет равно

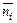(N)=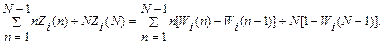

Перегруппируем члены суммы, приведем подобные:

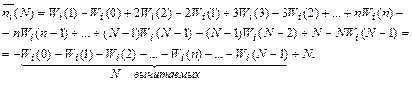
Еще раз перегруппируем члены, окончательно получим

                                          

(26)

                                (26)

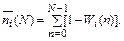
Для того чтобы определить математическое ожидание 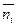 числа шагов до достижения поставленной цели (т. е. одного из состояния [А_r]) необходимо в формуле (26) снять ограничение по N, т. е. положить N = ¥. Тогда

                                            

(27)

                                     (27)

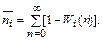
* Для определения 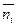 использована разработанная академиком А. Н. Кол­могоровым методика расчета математического ожидания числа попаданий, необ­ходимого для поражения цели.

При однородной цепи часто оказывается возможным получить конечные выражения для вычисления 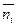. В общем же случае процедура вы­числения  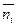на ЭВМ предусматривает прекращение суммирова­ния на N-м шаге при выполнении условия

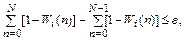
где e – малое положительное число, характеризующее требуемую точность расчетов.

Рассмотрим пример.

Пример 9. В условиях примера 7, «а» и «б» определить мате­матическое ожидание числа шагов до достижения конечного со­стояния А_т из состояния А₁ (пример 7, а) и из состояния А₁ и А₂ (пример 7, 6).

а) Предварительно найдем W₁(п) – вероятность достижения состояния А₂ из состояния А₁ за п шагов:

      

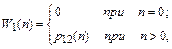
где                         p₁₂(n) = 1 – p₁₁ⁿ.

Тогда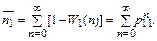            

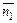(28)

Таким образом,  есть сумма членов бесконечно убывающей геометрической прогрессии.

Поэтому 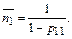                                                                      (28)

В условиях примера 7, а  математическое ожидание числа шагов равно

                                                 

(29)

                                             (29)

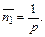
б) Первоначально определим вероятности W₁(п) и W₂(п) до­стижения состояния А₃ за п шагов из состояний А₁ и А₂ соответ­ственно:

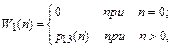
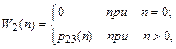
где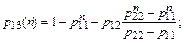            

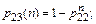
р₁₁ = 1 – р' – р" ; р₁₂ = р" ; р₂₂ = 1 – р"' ; р₂₃ = р"'.

После этого для определения 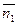 и 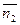 могут быть получены сле­дующие выражения:

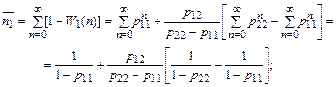(30)

                 (30)

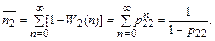(31)

                                                     (31)

Подставим в полученные выражения (30), (31) исход­ные данные из примера 7, б. Тогда

 ; .

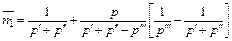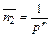Во всех рассмотренных выше случаях предполагалось, что мо­делируемый процесс достоверно начинается из состояния А_i. В том же случае, когда задано распределение начальных состоя­ний, будем иметь

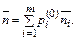(32)

                                                                                           (32)

где p_i⁽⁰⁾ – вероятности нахождения системы в i-х начальных состояниях, т – количество состояний, 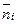- математическое ожидание количества шагов до достижения поставленной цели, если процесс начат из состояния А_i, 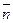- математическое ожидание количества шагов до достижения поставленной цели, если задано распределение вероятностей начала процесса из возможных состоя­ний.

Математическое ожидание времени, необходи­мого для достижения цели действий определяется из выражения

                                               

(33)

                                                (33)

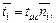
если известно состояние А_i  системы, при котором начинается процесс, и

                                            

(34)

                                              (34)

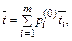
если задано распределение начальных состояний системы.

В этих выражениях t_ш – математическое ожидание промежут­ка времени между очередными шагами процесса.

Математическое ожидание ущерба, причиняе­мого противнику или своим силам за заданное число шагов процесса определяется по-разному для двух различных случаев:

1)  оценивается ущерб, причиняемый каким-то элементам системы;

2)  оценивается ущерб, причиняемый элемен­там, не входящим непосредственно в состав системы.

Методы вычислений рассмотрим на примерах.

Пример 10. Планируется ряд последовательных ударов авиа­ции по конвою, состоящему из т транспортов и эскорта. В каж­дом ударе принимает участие одинаковое число самолетов, исполь­зующих одно и то же оружие. До удара авиации конвой подвергся удару подводных лодок; распределение числа пораженных ими транспортов задано. Цель ударов авиации – поражение максимально возможного числа транспортов. Цель моделирования – определение зависимо­сти причиняемого противнику ущерба от числа ударов для обосно­вания потребного ресурса авиации.

Показателем эффективности ударов является математическое ожидание числа пораженных транспортов. Моделируемый процесс представляет собой дискретную цепь Маркова.

Системой является конвой, который в результате каждого удара может находиться в одном из т+1 состояний А₀, А₁, А₂, …, А_j, …, А_m, чему соответ­ствует 0, 1, ..., j , ..., т потерянных транспортов (для упрощения этого примера принимается, что каждому из состояний конвоя соответствует некоторое среднее число пораженных кораблей эскорта). Шагом про­цесса является очередной удар авиации, моментом шага – время нанесения удара.

Рассматриваемая цепь является цепью с невосстанавливаемым ущербом. Матрица перехода такой цепи имеет уже рассмотрен­ный выше вид верхней треугольной матрицы:

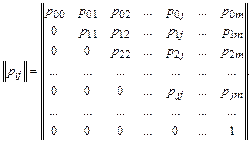(35)

                                          (35)

Задан вектор-строка начальных состояний

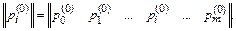
Найдем способ определения показателя эффективности – матема­тического ожидания числа пораженных транспортов – с помощью известных матрицы ||р _{i , j} || и вектора-строки ||р _i⁽⁰⁾||.

Обратим внимание, что ущерб, причиняемый противнику, – это пораженные транспорты конвоя. Они являются элементом мо­делируемой системы. Таким образом, имеет место первый из рас­сматриваемых случаев.

Используя методы, изложенные ранее, опреде­лим матрицу переходов за п шагов

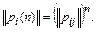
а затем учтем начальное состояние системы и получим вектор-строку

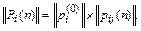
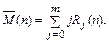(36)

Искомое математическое ожидание числа пораженных транспор­тов будет равно

                                                                                    (36)

Пример 11. В условиях примера 10 требуется определить математическое ожидание числа своих самолетов, поражаемых средствами ПВО конвоя.

В данном случае оценивается ущерб, наносимый элементам, не входящим непосредственно в систему, т. е. имеет место второй из рассматриваемых случаев. Дополним матрицу перехода (35) матрицей ущерба

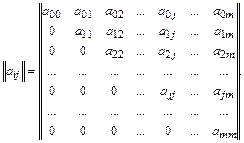(37)

                                            (37)

Параметр а_ij есть математическое ожидание числа своих са­молетов, потеря которых сопутствует переходу системы из состоя­ния A_i  в состояние A_j. Иначе говоря, с вероятностью р _ij  матема­тическое ожидание числа потерянных при очередном ударе само­летов равно а_ij, если только очередной удар начат из состоя­ния A_i.

Параметры а_ij  определяются с помощью моделей, порядок разработки которых рассматривается в книге Вентцель Е. С. «Исследование операций» (М., «Советское Радио», 1972).

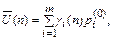(38)

Математическое ожидание ущерба (в данном случае числа по­терянных самолетов) будет равно 

                                                                                   (38)

где g_i(п) – математическое ожидание ущерба за п шагов процес­са, если процесс начат из состояния A_i.

Параметр g_i(п) определяется из рекуррентного соотношения

                                  

(39)

                            (39)

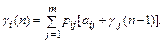
Смысл полученного выражения следующий: если система свой п-й шаг начала из состояния A_i, то с вероятностью р _ij  она перей­дет в состояние A_j (j= 1, 2, ... , т). При этом ущерб будет ра­вен сумме ущерба на п-м шаге (т. е. а_ij) и ущерба за п – 1 шагов, начинаемых из состояния A_j (т. е. g_i (п –1)).

Формула (38) может использоваться для опреде­ления не только своего ущерба, но и ущерба, причиняемого противнику. Так, в рассмотренном примере по этой формуле можно оценить потери истребительной авиации ПВО конвоя. Для этого при расчетах по формуле (38) вместо матрицы ||а_ij|| своих потерь должна ис­пользоваться матрица ||а_ij¢|| математического ожидания числа ис­требителей, теряемых противником при переходе системы из со­стояния A_i  в состояние A_j.

В области экономики рассмотренный метод используется для оценки дохода или ущерба предприятий, отраслей хозяйства.

В заключение рассмотрения вопроса о методах определения показателей эффективности дискретных цепей Маркова отметим, что рассмотренные выше показатели являются лишь наиболее часто употребляемыми в оперативно-тактической области, но отнюдь не единственными.

 

Подготовка к моделированию процессов боевых действий

методами теории дискретных цепей Маркова

Специфической особенностью методов теории дискретных це­пей Маркова является сравнительная простота разработки стан­дартных процедур для вычисления показателей эффективности на ЭВМ.

Если определены матрицы переходов ||р _{i , j}^(k)||; вектор-строка на­чальных состояний ||р _i⁽⁰⁾||, матрица ущерба ||а_{i , j} ||, то вычисление показателей эффективности может быть осуществлено с помощью заранее подготовленных процедур.

Подготовка к моделированию процессов боевых действий, описываемых дискретными цепями Маркова, производится на основании опера­тивно-тактической постановки задачи.

Целесообразна следующая последовательность операций при подготовке к моделированию:

1. Определить основной и дополнительные показатели эффек­тивности.

2. Разработать замысел моделирования: определить потребные варианты расчетов; параметры управления для каждого из вари­антов; рациональную последовательность смены 'вариантов.

3. Дать формализованное описание моделируемого процесса с целью определить:

- что есть система;

- каковы возможные состояния системы;

- что есть шаг процесса, и в какие моменты времени осуществ­ляются шаги;

- в какие состояния способна переходить система за один шаг из каждого своего состояния.

Если окажется, что в рамках поставленной задачи имеет ме­сто последействие (т. е. зависимость исхода очередного шага от пре­дыстории процесса), то следует откорректировать постановку задачи, увеличить число состояний так, чтобы добиться «марковости» про­цесса.

Полезно завершить формализованное описание задачи разра­боткой графа переходов цепи Маркова за один шаг. Всякий граф состоит из вершин и дуг. Вершины обозначают состояния системы, дуги – все возможные направления переходов из каждого состоя­ния системы за один шаг. Вершины обозначаются кружками, дуги стрелками. Если система в результате одного шага способна оста­ваться в данном состоянии, это обозначается стрелкой, выходящей из соответствующего кружка и входящей в него же. Рядом со стрелками записываются вероятности соответствующих переходов системы.

4. Разработать матрицы перехода ||р _{i , j}^(k)|| для всех п шагов и, при необходимости, матрицы ущерба ||а_{i , j} ||. Заполнять эти матрицы целесообразно, используя граф.

5. Определить значения исходных данных.

Примеры решения задач по моделированию процессов

боевых действий методами теории дискретных цепей Маркова

и определению показателей эффективности [4]

Пример 12. По групповой надводной цели противника, состоящей из трех однотипных кораблей, предполагается нанести последовательно удары: сначала один удар авиацией, а затем один удар ракетными катерами. Вероятности исходов удара авиацией:

- не поражена ни одна цель из двух или из трех – 0,05;

- поражены 3 цели из 3-х – 0,15;

- поражены 2 цели из 3-х – 0,30, 2 цели из 2-х – 0,35;

- поражена 1 цель из 3-х – 0,50; 1 цель из 2-х – 0,60; 1 цель из 1-й – 0,80.

Вероятности исходов удара ракетными катерами:

- не поражена ни одна цель – 0,10;

- поражены 3 цели из 3-х – 0,20;

- поражены 2 цели из 3-х – 0,30, 2 цели из 2-х – 0,40;

- поражена 1 цель из 3-х – 0,40; 1 цель из 2-х – 0,55; 1 цель из 1-й – 0,70.

Разработать математическую модель для определения значений показателей эффективности после нанесения по противнику ударов авиацией и ракетными катерами:

- вероятность поражения трех целей;

- вероятность поражения не менее двух целей;

- математическое ожидание числа пораженных целей;

Решение:

1. Цель удара – уничтожение всех кораблей противника. Цель моделирования - определения значений показателей эффективности после нанесения по противнику ударов сначала авиацией, а затем ракетными катерами. Шаг процесса - нанесение удара по противнику авиацией или ракетными катерами. В систему входят три корабля противника. Состояние системы до удара и после каждого удара будет характеризоваться числом объектов, сохранивших боеспособность к последующему удару. В данной задаче состояниями системы будут состояния, показанные на рисунке:

- А₀ – ни один корабль противника не поражен;

- А₁ – поражен один корабль противника;

- А₂ – поражены два корабля противника;

- А₃ – поражены три корабля противника.

Начальным состоянием будем считать состояние А₀, в котором система находится до нанесения ударов с вероятностью 1. Процесс нанесения последовательных ударов может быть ин­терпретирован как дискретная цепь Маркова с невосстанавливаемым ущербом. Граф переходов системы представлен на рисунке 3.4.4.

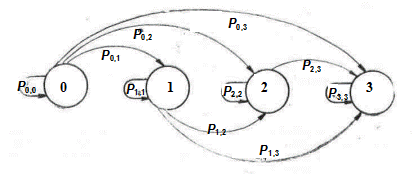
Рис. 3.4.4. Графическое представление модели задачи

В соответствии с заданными вероятностями исходов ударов матрицы переходов при нанесении удара авиацией и удара ракетны­ми катерами имеют следующий вид:

 

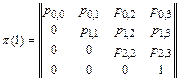
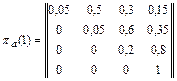
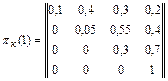
Для определения вероятностей исходов Р _ij(2) за два удара необхо­димо перемножить матрицы p_а(1) и p_к(1) в заданной последовательности нане­сения ударов.

.

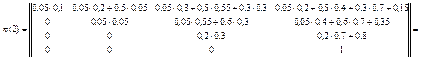
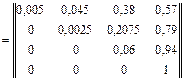После нахождения вероятностей Р_1j(2) всех возможных переходов из первого состояния в одно из трех состояний (j = 2, 3, 4) за два удара определяются значения показателей эффектив­ности:

- вероятность поражения трех целей p₀₃(2) = 0,57;

- вероятность поражения не менее двух целей 

p₀₂(2) + p₀₃(2)=0,38 + 0,57 = 0,95;

- математическое ожидание числа пораженных целей М(2) при нанесении удара сначала авиацией, а затем ракетными катерами вычисляется по следующей формуле, в которой m – количество пораженных целей противника: М(2) = 2,92 корабля:

=

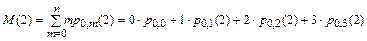= 0×0,005 + 1×0,045 + 2×0,38 + 3×0,57 = 0,045 + 0,76 + 1,71 = 2,515.

Пример 13. Решить ту же задачу, но с другими исходными данными: известны лишь вероятности уничтожения одного корабля противника авиацией p_а = 0,5 и ракетными катерами p_к = 0,6, а вероятности исходов удара необходимо вычислить, если вероятности поражения одного корабля противника авиацией и ракетными катерами не изменяются с уничтожением 1-го или 2-х кораблей из трех.

Решение:

 Определим элементы матрицы переходов при нанесении удара авиацией:

p_0,0а(1) = (1 – p_а)³ = 0,125– вероятность не поражения ни одного из трех кораблей за один удар;     

p_0,1а(1) = 3 p_а (1 – p_а) (1 – p_а) = 0,375 – вероятность поражения одного из трех кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_0,2а(1) =3 p_а × p_а(1 – p_а) = 0,375 – вероятность поражения двух кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_0,3а(1) = p_а × p_а × p_а = 0,125 – вероятность поражения двух кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_1,1а(1) = (1 – p_а)² = 0,25 – вероятность того, что если до нанесения удара один корабль был поражен, а два не поражены, то после удара так все и осталось.

P_1,2а(1) =2 p_а(1 – p_а) = 0,5 – вероятность перехода за один удар в состояние, когда поражены два из трех кораблей при условии, что до нанесения удара один корабль был уже поражен, а два еще не поражены.

P_1,3а(1) = p_а × p_а = 0, 25 – вероятность перехода за один удар в состояние, когда поражены все три корабля при условии, что до нанесения удара один корабль был уже поражен, а два еще не поражены.

P_2,2а(1) =1 – p_а = 0,5 – вероятность остаться за один удар в том же состоянии что и до удара, когда уже поражены два из трех кораблей , а один еще не поражен.

P_2,3а(1) = p_а = 0,5 – вероятность перехода за один удар в состояние, когда поражены все три корабля при условии, что до нанесения удара два корабля были уже поражены, а один еще не поражен.

Определим элементы матрицы переходов при нанесении удара ракетными катерами:

    p_0,0к(1) = (1 – p_к)³ = 0,064 – вероятность не поражения ни одного из трех кораблей за один удар;     

p_0,1к(1) = 3 p_к (1 – p_к) (1 – p_к) = 0,288 – вероятность поражения одного из трех кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_0,2к(1) =3 p_к × p_к(1 – p_к) = 0,432 – вероятность поражения двух кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_0,3к(1) = p_к × p_к × p_к = 0,216 – вероятность поражения двух кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_1,1к(1) = (1 – p_к)² = 0,16 – вероятность того, что если до нанесения удара один корабль был поражен, а два не поражены, то после удара так все и осталось.

P_1,2к(1) =2 p_к(1 – p_к) = 0,48 – вероятность перехода за один удар в состояние, когда поражены два из трех кораблей при условии, что до нанесения удара один корабль был уже поражен, а два еще не поражены.

P_1,3к(1) = p_к × p_к = 0, 36 – вероятность перехода за один удар в состояние, когда поражены все три корабля при условии, что до нанесения удара один корабль был уже поражен, а два еще не поражены.

P_2,2к(1) =1 – p_к = 0,4 – вероятность остаться за один удар в том же состоянии что и до удара, когда уже поражены два из трех кораблей , а один еще не поражен.

P_2,3к(1) = p_к = 0,6 – вероятность перехода за один удар в состояние, когда поражены все три корабля при условии, что до нанесения удара два корабля были уже поражены, а один еще не поражен.

 

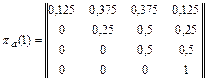
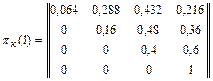
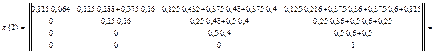
p(2)=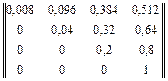

После нахождения вероятностей Р_1j(2) всех возможных переходов из первого состояния в одно из трех состояний (j = 2, 3, 4) за два удара определяются значения показателей эффектив­ности:

- вероятность поражения трех целей p₀₃(2) = 0,512

- вероятность поражения не менее двух целей p₀₂(2) + p₀₃(2)=0,384+ 0,512 = 0,896;

- математическое ожидание числа пораженных целей М(2) при нанесении удара сначала авиацией, а затем ракетными катерами вычисляется по следующей формуле, в которой m – количество пораженных целей противника: М(2) = 2,4 корабля:

=

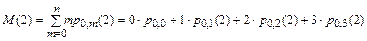= 0×0,008 + 1×0,096 + 2×0,384 + 3×0,512 = 0,096 + 0,768 + 1,536 = 2,4.

 

Пример 14. Решить ту же задачу (что и в примере 13), но считать, что вероятности поражения одного корабля противника авиацией и ракетными катерами изменяются с уничтожением 1-го или 2-х кораблей из трех:

– вероятности поражения одного корабля противника авиацией при условии, что все три корабля противника боеспособны: p_а(1/3) = 0,2,

– вероятности поражения одного корабля противника авиацией при условии, что два корабля противника боеспособны, а один уничтожен: p_а(1/2) = 0,3,

– вероятности поражения одного корабля противника авиацией при условии, что один корабль противника боеспособен, а два уничтожены: p_а(1/1) = 0,4;

– вероятности поражения одного корабля противника ракетными катерами при условии, что все три корабля противника боеспособны: p_к(1/3) = 0,25,

– вероятности поражения одного корабля противника ракетными катерами при условии, что два корабля противника боеспособны, а один уничтожен: p_к(1/2) = 0,35,

– вероятности поражения одного корабля противника ракетными катерами при условии, что один корабль противника боеспособен, а два уничтожены: p_к(1/1) = 0,45.

Решение:

Определим элементы матрицы переходов при нанесении удара авиацией:

p_0,0а(1) = (1 – p_а(1/3))³ = 0,8³=0,512 – вероятность не поражения ни одного из трех кораблей за один удар;     

p_0,1а(1) = 3 p_а(1/3) (1 – p_а(1/3)) (1 – p_а(1/3)) = 3×0,2×0,64=0,384 – вероятность поражения одного из трех кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_0,2а(1) =3 p_а(1/3) × p_а(1/3) (1 – p_а(1/3)) = 3×0,04×0,8=0,096 – вероятность поражения двух кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_0,3а(1) = p_а(1/3) × p_а(1/3) × p_а(1/3) = 0,2³=0,008 – вероятность поражения двух кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_1,1а(1) = (1 – p_а(1/2))² = 0,7² = 0,49 – вероятность того, что если до нанесения удара один корабль был поражен, а два не поражены, то после удара так все и осталось.

P_1,2а(1) =2 p_а(1/2) (1 – p_а(1/2)) = 2×0,3×0,7=0,42 – вероятность перехода за один удар в состояние, когда поражены два из трех кораблей при условии, что до нанесения удара один корабль был уже поражен, а два еще не поражены.

P_1,3а(1) = p_а(1/2) × p_а(1/2) = 0,3² = 0,09 – вероятность перехода за один удар в состояние, когда поражены все три корабля при условии, что до нанесения удара один корабль был уже поражен, а два еще не поражены.

P_2,2а(1) =1 – p_а(1/1) = 0,6 – вероятность остаться за один удар в том же состоянии что и до удара, когда уже поражены два из трех кораблей , а один еще не поражен.

P_2,3а(1) = p_а(1/1) = 0,4 – вероятность перехода за один удар в состояние, когда поражены все три корабля при условии, что до нанесения удара два корабля были уже поражены, а один еще не поражен.

 

Определим элементы матрицы переходов при нанесении удара ракетными катерами:

    p_0,0к(1) = (1 – p_к(1/3))³ = 0,75³=0,421875 – вероятность не поражения ни одного из трех кораблей за один удар;     

p_0,1к(1) = 3 p_к(1/3) (1 – p_к(1/3)) (1 – p_к) = 3×0,25×0,75²=0,421875 – вероятность поражения одного из трех кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_0,2к(1) =3 p_к(1/3) × p_к(1/3) (1 – p_к(1/3)) = 3×0,25²×0,75=0,140625 – вероятность поражения двух кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_0,3к(1) = p_к(1/3) × p_к(1/3) × p_к(1/3) = 0,25³=0,015625 – вероятность поражения двух кораблей за один удар при боеспособности всех трех кораблей до нанесения удара;

p_1,1к(1) = (1 – p_к(1/2))² = 0,65²=0,4225 – вероятность того, что если до нанесения удара один корабль был поражен, а два не поражены, то после удара так все и осталось.

P_1,2к(1) =2 p_к(1/2) (1 – p_к(1/2)) =2×0,35×0,65=0,455 – вероятность перехода за один удар в состояние, когда поражены два из трех кораблей при условии, что до нанесения удара один корабль был уже поражен, а два еще не поражены.

P_1,3к(1) = p_к(1/2) × p_к(1/2) = 0, 35² = 0,1225 – вероятность перехода за один удар в состояние, когда поражены все три корабля при условии, что до нанесения удара один корабль был уже поражен, а два еще не поражены.

P_2,2к(1) =1 – p_к(1/1) = 0,55 – вероятность остаться за один удар в том же состоянии что и до удара, когда уже поражены два из трех кораблей , а один еще не поражен.

P_2,3к(1) = p_к(1/1) = 0,45 – вероятность перехода за один удар в состояние, когда поражены все три корабля при условии, что до нанесения удара два корабля были уже поражены, а один еще не поражен.

В соответствии с рассчитанными вероятностями исходов ударов матрицы переходов при нанесении удара авиацией и удара ракетны­ми катерами, а также матрица переходов за два шага имеют следующий вид:

 

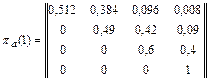
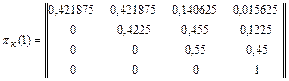
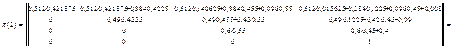
p(2)=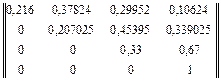

- вероятность поражения трех целей  p₀₃(2) = 0,10624;

- вероятность поражения не менее двух целей 

p₀₂(2) + p₀₃(2)=0,29952 + 0,10624= 0,40576;

- математическое ожидание числа пораженных целей М(2) при нанесении удара сначала авиацией, а затем ракетными катерами вычисляется по следующей формуле, в которой m – количество пораженных целей противника: М(2) = 1,29636 корабля:

=

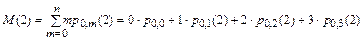= 0×0,216 + 1×0,37824 + 2×0,29952 + 3×0,10624 = 0,37824 + 0,59904 + 0,31872 = 1,29636.

Пример 15. При наличии всего двух кораблей противника определить оценку математического ожидания числа ударов только авиацией, необходимого для поражения обоих кораблей противника, если вероятность уничтожения за один удар одного корабля противника из двух боеспособных до нанесения удара p_а(1/2) = 0,3, а вероятность уничтожения за один удар одного корабля противника при пораженном втором корабле p_а(1/1) = 0,4.

Решение:

Т. к. p_0,0(n) + p_0,1(n) + p_0,2(n) =1, то 1 – p_0,2(n) = p_0,0(n) + p_0,1(n). Т. е. после одного удара возможна только одна из трех ситуаций (состояний системы): не поражен ни один корабль (вероятность p_0,0(1)); один корабль поражен, а второй боеспособен (вероятность p_0,1(1)); оба корабля поражены (вероятность p_0,2(1)). Матрица переходов за один шаг выглядит так:

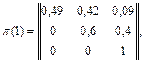
где p_0,0(1) = (1 – p_а(1/2))² = 0,49 – вероятность не поражения ни одного из двух кораблей за один удар;     

p_0,1(1) = p_а(1/2) (1 – p_а(1/2)) + p_а(1/2) (1 – p_а(1/2)) = 0,42 – вероятность поражения одного из двух кораблей за один удар при непораженном другом корабле;

p_1,1(1) = 1 – p_а(1/1) = 0,6 – вероятность того, что если до нанесения удара один корабль был поражен, а другой не поражен, то после удара так все и осталось.

1 – p_а(1/2) – вероятность не поражения одного корабля из двух боеспособных за один удар;

(1 – p_а(1/2))² – вероятность не поражения обоих кораблей за один удар;

p_а (1 – p_а(1/2)) – вероятность не поражения первого корабля при поражении второго;

p_а (1 – p_а(1/2)) – вероятность не поражения второго корабля при поражении первого.

Формула, для вычисления оценки математического ожидания числа (среднего числа) ударов, необходимого для поражения обоих кораблей противника, выглядит следующим образом:

.

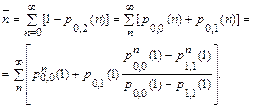
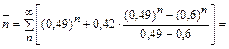
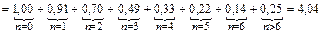Подставляя в формулу значения вероятностей соответствующих переходов системы, получим:

Ответ: Оценка математического ожидания числа ударов авиацией по кораблям противника, необходимого для поражения обоих кораблей при заданных условных вероятностях поражения одного корабля 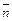= 4,04 ударов.

 

Упражнения:

1. По групповой надводной цели противника, состоящей из трех однотипных кораблей, предполагается нанести последовательно удары: сначала один удар ракетными катерами, а затем один удар авиацией. Вероятности исходов удара авиацией:

- не поражена ни одна цель из одной, из двух или из трех – 0,08;

- поражены 3 цели из 3-х – 0,15;

- поражены 2 цели из 3-х – 0,32, 2 цели из 2-х – 0,33;

- поражена 1 цель из 3-х – 0,45; 1 цель из 2-х – 0,59; 1 цель из 1-й – 0,92.

Вероятности исходов удара ракетными катерами:

- не поражена ни одна цель из одной, из двух или из трех – 0,08;

- поражены 3 цели из 3-х – 0,21;

- поражены 2 цели из 3-х – 0,31, 2 цели из 2-х – 0,35;

- поражена 1 цель из 3-х – 0,40; 1 цель из 2-х – 0,57; 1 цель из 1-й – 0,98.

Разработать математическую модель для определения значений показателей эффективности после нанесения по противнику ударов ракетными катерами и авиацией:

- вероятность поражения трех целей;

- вероятность поражения не менее двух целей;

- математическое ожидание числа пораженных целей.

Определить, какая очередность применения ударов более эффективна: сначала катера, затем авиация, или сначала авиация, а потом катера.

2. Решить ту же задачу, но с другими исходными данными: известны лишь вероятности уничтожения одного корабля противника авиацией p_а = 0,5 и ракетными катерами p_к = 0,55, а вероятности исходов удара необходимо вычислить, если вероятности поражения одного корабля противника авиацией и ракетными катерами не изменяются с уничтожением 1-го или 2-х кораблей из трех.

3. Решить ту же задачу (что и 2), но считать, что вероятности поражения одного корабля противника авиацией и ракетными катерами изменяются с уничтожением 1-го или 2-х кораблей из трех:

– вероятности поражения одного корабля противника авиацией при условии, что все три корабля противника боеспособны: p_а(1/3) = 0,25,

– вероятности поражения одного корабля противника авиацией при условии, что два корабля противника боеспособны, а один уничтожен: p_а(1/2) = 0,35,

– вероятности поражения одного корабля противника авиацией при условии, что один корабль противника боеспособен, а два уничтожены: p_а(1/1) = 0,45;

– вероятности поражения одного корабля противника ракетными катерами при условии, что все три корабля противника боеспособны: p_к(1/3) = 0,30,

– вероятности поражения одного корабля противника ракетными катерами при условии, что два корабля противника боеспособны, а один уничтожен: p_к(1/2) = 0,35,

– вероятности поражения одного корабля противника ракетными катерами при условии, что один корабль противника боеспособен, а два уничтожены: p_к(1/1) = 0,40.

4. При наличии всего двух кораблей противника определить оценку математического ожидания числа ударов только авиацией, необходимого для поражения обоих кораблей противника, если вероятность уничтожения одного корабля противника p_а(1/2) = p_а(1/1) = 0,5.

Контрольные вопросы:

1. Дать определение случайного процесса и динамики боя.

2. Дать определение стационарного и нестационарного процессов.

3. Дать определение Марковского случайного процесса.

4. Приведите примеры оперативно-тактических ситуаций, для моделирования которых могут быть использованы дискретные цепи Маркова.

5. Что должен выявить исследователь при постановке задачи для ее решения методами теории дискретных цепей Маркова?

6. Каким образом не Марковский процесс можно представить как Марковский?

7. Сформулировать правило определения элементов обстановки, которые должны включаться в понятие система при постановке задачи для ее решения методами теории дискретных цепей Маркова.

8. Перечислить показатели эффективности, вычисляемые методами теории дискретных цепей Маркова.

9. Дать определение однородной и неоднородной цепи Маркова.

10. Сформулировать правило вычисления матрицы переходов за n шагов.

11. Какова должна быть сумма элементов строки матрицы переходов?

12. Как вычислить значение элемента матрицы, являющейся произведением двух квадратных матриц?

13. Дать определение дискретной цепи Маркова с невосстанавливаемым ущербом.

14. За счет чего упрощаются формулы для вычисления элементов матрицы переходов за n шагов в дискретной цепи Маркова с невосстанавливаемым ущербом?

15. Какие дискретные цепи Маркова называются эргодическими?

16. Дать определение стационарного режима эргодической цепи Маркова.

17. В чем заключается метод определения предельных вероятностей переходов в эргодической цепи Маркова?

18. Как определяется вероятность достижения цели за заданное число шагов?

19. Как определяется вероятность достижения цели на заданном шаге?

20. Как вычисляется математическое ожидание числа шагов, необходимых для достижения цели?

21. Как вычисляется математическое ожидание времени, необходимого для достижения цели?

22. Как вычисляется математическое ожидание ущерба, наносимого нами противнику или противником нам, за заданное число шагов?

23. Приведите последовательность операций, выполняемых при подготовке к моделированию процессов боевых действий методами теории дискретных цепей Маркова.