И несколько шагов

Основу математической модели цепи Маркова составляют мат­рицы вероятностей переходов системы в возможные состояния за каждый из шагов. В дальнейшем для краткости будем называть их просто матрицами переходов.

Рассмотрим свойства матрицы перехода за один шаг. Обозна­чим через 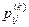 вероятности того, что система, которая перед оче­редным (k-м) шагом была в состоянии А_i, в результате k -го шага перейдет в состояние А_j (i = 1, 2, ... , m; j = 1, 2, ... , m).

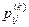Если вероятности переходов меняются от шага к шагу, цепь Маркова называется неоднородной.

Если же вероятности 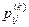одинаковы для всех шагов, цепь Маркова называется однородной. В этом случае вероятности перехода принято обозначать .

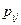Матрица вероятностей переходов за один шаг имеет следующий вид:

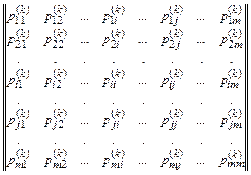
Как видно, матрица вероятностей переходов квадратная, т. е. число строк равняется числу столбцов. Каждый элемент i-й строки матрицы (i = 1, 2, . . . , т) есть вероятность того, что система, которая до k-го шага была в состоянии A_i, после k-го шага перейдет в состоя­ние, номер которого соответствует номеру столбца матрицы.

Например:

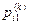– вероятность того, в ре­зультате k-го шага система перейдет из состояния A_i в состояние A₁;

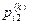– вероятность того, в ре­зультате k-го шага система перейдет из состояния A_i в состояние A₂;

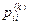– вероятность того, в ре­зультате k-го шага система перейдет из состояния A_i в состояние A_i (т. е. вероятность того, что система останется в состоянии A_i);

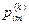– вероятность того, в ре­зультате k-го шага система перейдет из состояния A_i в состояние A_m;

Так как система в результате k-го шага обязательно должна оказаться в одном из т состояний, то сумма вероятностей каждой из строк равняется единице:

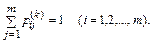
Это свойство часто используется для проверки правильности за­полнения матрицы переходов.

Элементы j-го столбца матрицы переходов (j = 1, 2, ... , т) представляют собой условные вероятности перехода системы в ре­зультате k-го шага в состояния А_j, вычисленные при условии, что перед k-м шагом система находилась в состоянии A_i.

В зависимости от особенностей процесса некоторые из вероят­ностей 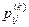 могут быть равны нулю, что означает невозможность перехода системы на k-м шаге из состояния A_i в состояние А_j.

Знание матрицы перехода за один шаг позволяет определить элементы р _ij(п) матрицы переходов за п шагов.

· Через р _ij(п) обозначается вероятность того, что система, бывшая перед первым шагом в состоянии A_i, в результате п шагов (т. е. после п шагов) процесса перейдет в состояние А_j.

Матрица переходов за п шагов определяется в результате по­следовательного матричного перемножения п матриц.

Обозначим через p_k или 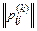 матрицу переходов для k-го ша­га, а через p(п) или  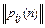– матрицу переходов в результате п шагов.

Символически матричное произведение для неоднородной цепи записывается следующим образом:

p(п)= p₁×p₂×…×p_k×…×p_n

или

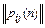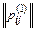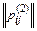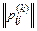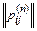                              = × ×…× ×…×             (1)

а для однородной цепи:

p(п)= p₁ⁿ

или

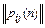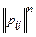                                            =                                         (2)

Смысл же матричного перемножения матриц переходов рас­смотрим на следующем примере.

Пример 6. Пусть заданы матрицы перехода на первом и вто­ром шагах:

Требуется определить матрицу .перехода за два шага

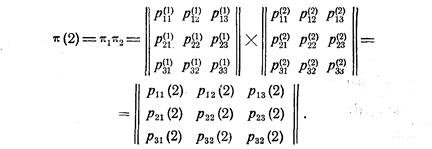
Определим, в качестве примера вероятность р₂₃(2) перехода системы за два шага из второго состояния в третье.

Относительно исходов первого шага системы мы можем только строить гипотезы. А именно, известно, что после первого шага си­стема может из состояния А₂ перейти в состояние A₁ или в состояние А₃, или остаться в состоянии А₂. Известны и вероятности этих гипотез. Ими являются соответственно вероятности , , .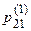

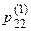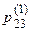Если реализуется гипотеза A₁, то искомое событие (переход системы в состояние А₃) произойдет с условной вероятностью 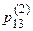, при гипотезе А₂ – с условной вероятностью  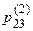и т. д.

Таким образом, можно использовать формулу полной вероят­ности

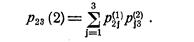
Обратим внимание, что процесс нахождения вероятности 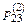 выглядит следующим образом: элементы второй строки матри­цы p₁ почленно умножаются на элементы третьего столбца мат­рицы p₂, затем суммируются найденные произведения.

Аналогичным образом определяются и остальные вероятности матрицы перехода p (2).

В общем виде формула для определения вероятностей перехо­дов системы за два шага имеет вид

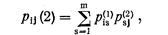
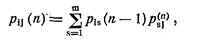
где p_is(п – 1) – вероятность перехода системы из состояния A_i в состояние A_s в результате шагов от первого до (п – 1)-го, или

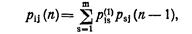
где p_sj (п – 1) – вероятность перехода системы из состояния A_s в состояние A_j в результате шагов от второго до п-го.

Соответственно двум предыдущим выражениям для матрицы p(п) переходов за п шагов справедливы выражения

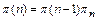                                                                                      (5)

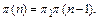                                                                                      (6)

Матрица переходов за п шагов обладает теми же свойствами, что и матрица переходов за один шаг.

Для перемножения матриц переходов на ЭВМ могут быть лег­ко разработаны стандартные процедуры.

Произведение матриц переходов не обладает переместительным свойством. В общем случае p₁ p₂ ¹ p₂ p₁. Это обстоятельство позволяет использовать цепи Маркова для обоснования важного элемента решений командира по поставленным задачам – опреде­ления оптимальной последовательности ударов или, шире, опти­мальной последовательности действий.