Исследуемый процесс может быть интерпретирован как дис­кретная цепь Маркова, если ему может быть дано следующее об­щее описание [3].

Имеется система, которая в каждый момент времени может находиться в одном из т состояний. Смена системой состояния (шаг процесса) осуществляется только в фиксиро­ванные момен­ты времени. Известны или могут быть вычислены вероятности то­го, что система, которая до очередного шага была в состоянии А_i       (i = 1, 2, ... , т), в результате этого шага перейдет в состояние А_j (j = 1, 2, ... , т). Вероятность того, что система ока­жется в любом состоянии за очередной шаг процесса зависит только от состояния сис­темы до очередного шага и не зависит от того, как именно система ока­залась в этом со­стоянии. Переходы системы в возможные состоя­ния составляют полную группу несовме­стных событий (в общем случае число состояний т может быть в принципе бесконечным, однако мы будем рассматривать только случай конечного числа т).

Если исследуемый процесс может быть описан подобным обра­зом, то для его моделирования могут быть использованы методы теория дискретных цепей Маркова.

Постановка задачи

Из изложенного выше также следует, что для применения методов теории дискретных цепей Маркова оперативно-тактическая постановка задачи долж­на быть сделана таким образом, чтобы имелась возможность вы­явить:

а) что является системой;

б) каковы возможные состояния системы;

в) что является шагом процесса, и в какие моменты времени осуществляются шаги;

г) какие переходы системы из состояния в состояние возмож­ны за один шаг.

Описание процесса должно также дать возможность опреде­лить вероятности переходов системы на каждом шаге.

Осуществляя оперативно-тактическую постановку задачи, сле­дует иметь в виду, что набор состояний системы, учитываемых в модели, определяется, в первую очередь, особенностями процесса. При этом в зависимости от целей действия сил и целей моделиро­вания некоторые состояния можно объединить в одно состояние и тем самым упростить модель. И наоборот, чтобы добиться «мар­ковости» процесса, т. е. возможности учитывать при определении вероятностей переходов системы только ее состояние до очеред­ного шага, часто оказывается необходимым «дробить», увеличи­вать число возможных состояний системы.

В принципе любой не Марковский процесс может быть представ­лен как Марковский за счет соответствующего увеличения числа состояний системы.

Рассмотрим некоторые примеры.

Пример 1. По группе кораблей противника, состоящей из ко­рабля ядра и двух кораблей охранения, планируется нанесений нескольких последовательных ударов ударными группами, приме­няющими различное оружие.

Различные виды оружия обладают разной вероятностью пора­жения корабля ядра и кораблей охранения, причем эта вероят­ность меняется в зависимости от числа боеспособных кораблей охранения.

Цель удара: поражение корабля ядра, цель моделирования: обоснование рациональной последовательности ударов.

В данном случае имеем:

а) Система – группа кораблей противника в составе корабля ядра и двух кораблей охранения.

б) Состояния системы:

А₁ – корабль ядра и корабли охранения не поражены;

А₂ – корабль ядра не поражен, один корабль охранения пора­жен,

А₃ – корабль ядра не поражен, оба корабля охранения пора­жены;

А₄ – корабль ядра поражен;

в) Шаг процесса: нанесение удара очередной ударной груп­пой; момент шага: момент нанесения удара.

г) Система за один шаг способна переходить из состояния с меньшим номером в одно из состояний с большим номером. Об­ратные переходы невозможны. Однако система способна в резуль­тате шага оставаться в прежнем состоянии. Данную задачу иллюстрирует граф переходов (рис. 3.4.1).

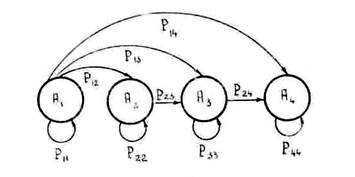
Рис. 3.4.1. Графическое представление модели задачи

Пример 2. В отличие от условий примера 1 целью ударов является поражение всех кораблей противника. В этом случае учитываемыми в модели состояниями системы являются:

А₁, А₂, А₃ – корабль ядра не поражен, поражены соответствен­но ноль, один, два корабля охранения;

А₄, А₅, А₆ – корабль ядра поражен, поражены соответственно ноль, один, два корабля охранения.

Пример 3. Если в условиях примера 1 считать, что вероятность поражения корабля ядра при очередном ударе существенно зависит от такого элемента «предыстории процесса», как поврежде­ния, полученные этим кораблем при предыдущих ударах, то необходимо ввести состояния системы, связанные с повреждением корабля ядра. Эти повреждения, например, могут требовать снижения скорости группы кораблей противника ниже определенного предела. В этом случае в модели требуется учесть следующие состояния системы:

А₁, А₂, А₃ – корабль ядра не поврежден, поражены соответ­ственно ноль, один, два корабля охранения;

А₄, А₅, А₆ – корабль ядра поврежден, поражены соответствен­но ноль, один, два корабля охранения;

А₇ — корабль ядра поражен.

В примере 1 по сравнению с примером 2 состояния А₄, А₅, А₆ объединены в одно состояние А₄. Различие в числе учитываемых состояний определяется различием в целях действия сил.

В примере 3 для сохранения «марковости» процесса введена группа состояний, учитывающих повреждение корабля ядра.

Пример 4. Подводная лодка передает сообщения на команд­ный пункт (КП), осуществляя для повышения надежности пере­дачи сообщения несколько повторных передач радиограммы (РДО) с одним и тем же сообщением.

В процессе передачи сообщения подводная лодка может быть обнаружена и атакована противолодочными силами противника. В этом случае выполнить запланированное число передач РДО подводная лодка может, только оторвавшись от преследования.

Цель использования средств связи подводной лодки – переда­ча на КП сообщения. Цель моделирования – обоснование луч­шего по надежности способа передачи подводной лодкой сообще­ния в условиях противодействия противолодочных сил противника.

В данном случае имеем:

а) Система – подводная лодка и КП.

б) Состояния системы:

А₁ – сообщение на КП не получено; подводная лодка противолодочными силами не поражена;

А₂ – сообщение на КП получено;

А₃ – сообщение на КП не получено; подводная лодка пораже­на противолодочными силами.

в) Шаг системы: передача подводной лодкой РДО. Шаг си­стемы имеет продолжительность, равную математическому ожида­нию промежутка времени между началами двух смежных передач РДО. При этом математическое ожидание времени уклонения под­водной лодки от преследования включается в продолжительность шага.

г) Система способна из состояния А₁ переходить в состоя­ние А₂ или А₃. Из состояний А₂ и А₃ переход ни в какие другие состояния невозможен, так как при этом моделируемый процесс заканчи­вается: в первом случае ввиду достижения цели действий, во вто­ром – из-за поражения подводной лодки. Возможно, что в резуль­тате шага система останется в прежнем состоянии.

Пример 5. Дополнительно к условиям примера 4 следует учесть, что возможность осуществления дальнейших передач РДО непораженной подводной лодкой существенно зависит от того, как подводная лодка пришла в состояние А₁. А именно: если под­водная лодка хотя бы один раз была обнаружена ранее, то против­ник усиливает противолодочную оборону в данном районе, отчего вероятность обнаружения подводной лодки возрастает.

В этом случае следует считать:

а) Система — подводная лодка, КП, противолодочные силы противника.

б) Состояния системы:

А₁ – сообщение на КП не получено, подводная лодка не пора­жена, ранее противником не обнаруживалась; противолодочная оборона в районе не усилена;

А₂ – сообщение на КП не получено, подводная лодка не пора­жена, противником ранее обнаруживалась; противник усилил противолодочную оборону в районе;

А₃ – сообщение на КП получено;

А₄ – сообщение на КП не получено, подводная лодка пораже­на противником.

в) Шаг системы: передача подводной лодкой РДО.

г) Система способна переходить из состояния А₁ или А₂ во все состояния с большим номером. Из состояний А₃ и А₄  переход ни в какие другие состояния невозможен. Данную задачу иллюстрирует граф переходов (рис. 3.4.2), в котором дополнительно к усло­виям задачи принято, что при состоянии системы А₂ противник прини­мает лишь меры, затрудняющие подводной лодке использовать средства радиосвязи).

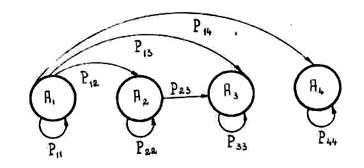
Рис. 3.4.2. Графическое представление модели задачи

Последний пример иллюстрирует следующее правило опреде­ления элементов обстановки, которые должны включаться в поня­тие система:

систему составляют все те элементы обстановки, ко­торые способны изменяться от шага к шагу, изменяя при этом возможность достижения цели действия сил. Элементы обстанов­ки, которые не способны изменяться в результате шага, но влияют на достижение цели действий (например, противолодочные силы противника в примере 4), учитываются при определении вероят­ностей переходов.

Заметим, что в приведенных выше примерах не рассматрива­лись способы определения необходимых вероятностей: поражения объектов противника, обнаружения подводной лодки и т. д. Мы будем счи­тать все необходимые вероятности событий известными.

Оперативно-тактическую постановку задачи осуществляет командир, а интерпретацию процесса как дискретной цепи Маркова должен осуществлять специалист по исследованию операций.

Вряд ли такой специалист будет находиться на корабле, поэтому и интерпретация процесса как дискретной цепи Маркова, и решение задачи должно быть возложено на БИУС. Для этого в БИУС:

- должна иметься достоверная и полная оперативная информация о противнике, а также своих силах и средствах,

- в базах данных БИУС должны храниться априорные вероятности наступления различных событий либо рассчитанные, либо полученные в результате накопления и обработки статистических данных,

- БИУС должна быть интеллектуальной системой, способной «понимать» поставленную командиром задачу и преобразовывать ее в форму, удобную для решения методами теории дискретных цепей Маркова.

Показатели эффективности, вычисляемые методами теории 

дискретных цепей Маркова

Рассматриваемые методы позволяют находить распределение состояний системы на различных шагах процесса. А это открыва­ет возможность с помощью методов теории вероятностей находить различные вероятностные характеристики, используемые в каче­стве показателей эффективности.

Обычно рассматриваемые методы применяются для опре­деления следующих вероятностных характеристик:

– вероятности того, что цель действия сил (своих или против­ника) будет достигнута за заданное число шагов или за заданное время процесса;

– вероятности того, что цель действия сил будет достигнута именно на заданном шаге или именно в заданный момент; 

– математического ожидания числа шагов, необходимых для достижения цели действий;

– математического ожидания времени, необходимого для до­стижения цели действий;

– математического ожидания ущерба, причиняемого против­нику, или ущерба, причиняемого противником нашим силам за заданное число шагов процесса.