
Существует класс цепей Маркова, отличающихся следующей особенностью: при достаточно большом числе шагов п вероятности перехода р i , j(п) системы в различные состояния перестают меняться от шага к шагу. При этом предельные вероятности переходов 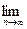 р i , j(п) = р j, существуют для всех значений i, j и не зависят от номера исходного состояния Аi. Цепи Маркова, обладающие подобными свойствами, называются эргодическими, а режим функционирования системы, при котором вероятности переходов неизменны, – стационарным режимом.
р i , j(п) = р j, существуют для всех значений i, j и не зависят от номера исходного состояния Аi. Цепи Маркова, обладающие подобными свойствами, называются эргодическими, а режим функционирования системы, при котором вероятности переходов неизменны, – стационарным режимом.
Частным случаем эргодических цепей являются рассмотренные выше цепи с невосстанавливаемым ущербом и одним поглощающим состоянием: при достаточно большом числе шагов система с вероятностью р m = 1 перейдет в поглощающее состояние Аm, из какого бы состояния ни начался процесс. Вероятность же нахождения системы во всех других состояниях Аj (j¹ m) будет при этом равна нулю. Матрицы переходов для таких цепей в стационарном режиме имеют следующий вид:
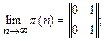
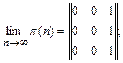
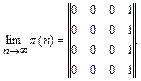
Заметим, однако, что если цепь с невосстанавливаемым ущербом имеет несколько поглощающих состояний или групп поглощающих состояний, то процесс не будет эргодическим, так как его исход будет зависеть от начального состояния системы.
Судить об эргодичности процесса можно по следующим признакам:
– по известным особенностям протекания процесса (например, дискретные цепи с невосстанавливаемым ущербом);
– по виду матрицы перехода. Типичными признаками являются: матрица переходов, состоящая только из положительных элементов р i , j, или же матрица переходов, у которой положительны все элементы главной диагонали и все элементы прилегающих к ней двух соседних диагоналей;
– если в результате возведения в степень п матрицы переходов ||рi,j|| будет выполнено условие:
рi,j(п) – р i,j(п – 1) £ e (i=1,2, ..., т; j=1,2, ..., т), (22)
где e – заданная малая положительная величина.
Существуют следующие методы определения вероятностей переходов эргодических цепей.
Для переходного режима функционирования цепи применяются методы, изложенные в 4 пункте 3-го вопроса лекции. Эти же методы могут быть использованы и при стационарном режиме. При этом процесс последовательного перемножения матриц должен сопровождаться проверкой условия (22). Выполнение этого условия на п-м шаге свидетельствует о том, что начался стационарный режим. Полученная матрица ||р i , j(п)||содержит предельные вероятности перехода. Однако существует и специальный метод определения предельных вероятностей переходов, к изложению которого мы и переходим.
Используем выражение (3):
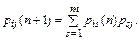
Для п, при котором имеет место условие 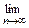 р i , j(п) = р j(п) = Pj, можем записать
р i , j(п) = р j(п) = Pj, можем записать
|
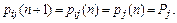 (23)
(23)
Поэтому
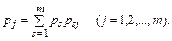
Таким образом, предельные вероятности переходов находятся из решения системы алгебраических уравнений (23). Эта система при т неизвестных имеет только т – 1 независимых уравнений, так как одно (любое) из уравнений системы может быть получено с помощью остальных благодаря условию
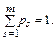
Поэтому система (23) дополняется этим условием.
Пример 8. Разрабатываются методы корректировки залпового артиллерийского огня по кораблю противника. Результатом каждого залпа может быть одно из следующих событий: А1 – недолет или перелет без выноса по целику; А2 – вынос по целику; А3 – накрытие.
Различным методам корректировки соответствуют различные вероятности указанных событий на залп, задаваемые матрицами перехода вида
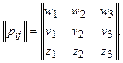
w1 – вероятность наступления в результате залпа события А1, если в результате предыдущего залпа наступило событие А1;
w2 – вероятность наступления в результате залпа события А2, если в результате предыдущего залпа наступило событие А1;
w3 – вероятность наступления в результате залпа события А3, если в результате предыдущего залпа наступило событие А1;
v1 – вероятность наступления в результате залпа события А1, если в результате предыдущего залпа наступило событие А2;
v2 – вероятность наступления в результате залпа события А2, если в результате предыдущего залпа наступило событие А2;
v3 – вероятность наступления в результате залпа события А3, если в результате предыдущего залпа наступило событие А2;
z1 – вероятность наступления в результате залпа события А1, если в результате предыдущего залпа наступило событие А3;
z2 – вероятность наступления в результате залпа события А2, если в результате предыдущего залпа наступило событие А3;
z3 – вероятность наступления в результате залпа события А3, если в результате предыдущего залпа наступило событие А3;
Все элементы р i , j таких матриц положительны.
Цель применения оружия – поражение корабля противника. Цель моделирования – обоснование лучшего метода корректировки огня из числа заданных методов.
Показателем эффективности стрельбы является вероятность поражения корабля противника. Однако при стационарном режиме этот показатель может быть заменен вероятностью накрытия цели залпом.
Стрельба на поражение (после окончания пристрелки) может рассматриваться именно как стационарный режим дискретной цепи. Об эргодичности цепи свидетельствует также характер матрицы перехода, все элементы которой положительны.
Для определения вероятностей различных исходов очередных залпов найдем предельные вероятности переходов. Составим систему уравнений
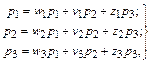
дополняемую условием р1 + р2 + р3 = 1.
Подставим в два первых уравнения вместо вероятности р3 ее значение, выраженное через вероятности р1 и р2:
р3 = 1 – р1 – р2.
Получим систему из двух уравнений с двумя 'неизвестными:

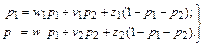
Решением этой системы будет
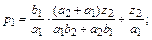
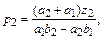
где a1=1–w1+z1; a2=w2–z2; b1=v1–z1; b2=1–v2+z2;
После этого может быть найдена вероятность
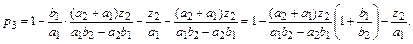
Показателем эффективности в данном случае является W = р3. Данную задачу иллюстрирует граф переходов (рис. 3.4.3)
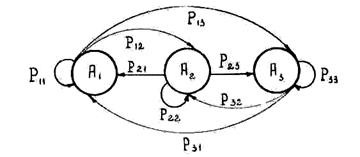
Рис. 3.4.3. Графическое представление модели задачи
Дата: 2019-03-05, просмотров: 314.