Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Понятие о дискретных цепях Маркова

Исследуемый процесс может быть интерпретирован как дис­кретная цепь Маркова, если ему может быть дано следующее об­щее описание [3].

Имеется система, которая в каждый момент времени может находиться в одном из т состояний. Смена системой состояния (шаг процесса) осуществляется только в фиксиро­ванные момен­ты времени. Известны или могут быть вычислены вероятности то­го, что система, которая до очередного шага была в состоянии А_i       (i = 1, 2, ... , т), в результате этого шага перейдет в состояние А_j (j = 1, 2, ... , т). Вероятность того, что система ока­жется в любом состоянии за очередной шаг процесса зависит только от состояния сис­темы до очередного шага и не зависит от того, как именно система ока­залась в этом со­стоянии. Переходы системы в возможные состоя­ния составляют полную группу несовме­стных событий (в общем случае число состояний т может быть в принципе бесконечным, однако мы будем рассматривать только случай конечного числа т).

Если исследуемый процесс может быть описан подобным обра­зом, то для его моделирования могут быть использованы методы теория дискретных цепей Маркова.

Постановка задачи

Из изложенного выше также следует, что для применения методов теории дискретных цепей Маркова оперативно-тактическая постановка задачи долж­на быть сделана таким образом, чтобы имелась возможность вы­явить:

а) что является системой;

б) каковы возможные состояния системы;

в) что является шагом процесса, и в какие моменты времени осуществляются шаги;

г) какие переходы системы из состояния в состояние возмож­ны за один шаг.

Описание процесса должно также дать возможность опреде­лить вероятности переходов системы на каждом шаге.

Осуществляя оперативно-тактическую постановку задачи, сле­дует иметь в виду, что набор состояний системы, учитываемых в модели, определяется, в первую очередь, особенностями процесса. При этом в зависимости от целей действия сил и целей моделиро­вания некоторые состояния можно объединить в одно состояние и тем самым упростить модель. И наоборот, чтобы добиться «мар­ковости» процесса, т. е. возможности учитывать при определении вероятностей переходов системы только ее состояние до очеред­ного шага, часто оказывается необходимым «дробить», увеличи­вать число возможных состояний системы.

В принципе любой не Марковский процесс может быть представ­лен как Марковский за счет соответствующего увеличения числа состояний системы.

Рассмотрим некоторые примеры.

Пример 1. По группе кораблей противника, состоящей из ко­рабля ядра и двух кораблей охранения, планируется нанесений нескольких последовательных ударов ударными группами, приме­няющими различное оружие.

Различные виды оружия обладают разной вероятностью пора­жения корабля ядра и кораблей охранения, причем эта вероят­ность меняется в зависимости от числа боеспособных кораблей охранения.

Цель удара: поражение корабля ядра, цель моделирования: обоснование рациональной последовательности ударов.

В данном случае имеем:

а) Система – группа кораблей противника в составе корабля ядра и двух кораблей охранения.

б) Состояния системы:

А₁ – корабль ядра и корабли охранения не поражены;

А₂ – корабль ядра не поражен, один корабль охранения пора­жен,

А₃ – корабль ядра не поражен, оба корабля охранения пора­жены;

А₄ – корабль ядра поражен;

в) Шаг процесса: нанесение удара очередной ударной груп­пой; момент шага: момент нанесения удара.

г) Система за один шаг способна переходить из состояния с меньшим номером в одно из состояний с большим номером. Об­ратные переходы невозможны. Однако система способна в резуль­тате шага оставаться в прежнем состоянии. Данную задачу иллюстрирует граф переходов (рис. 3.4.1).

 

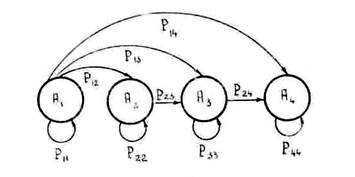
Рис. 3.4.1. Графическое представление модели задачи

Пример 2. В отличие от условий примера 1 целью ударов является поражение всех кораблей противника. В этом случае учитываемыми в модели состояниями системы являются:

А₁, А₂, А₃ – корабль ядра не поражен, поражены соответствен­но ноль, один, два корабля охранения;

А₄, А₅, А₆ – корабль ядра поражен, поражены соответственно ноль, один, два корабля охранения.

Пример 3. Если в условиях примера 1 считать, что вероятность поражения корабля ядра при очередном ударе существенно зависит от такого элемента «предыстории процесса», как поврежде­ния, полученные этим кораблем при предыдущих ударах, то необходимо ввести состояния системы, связанные с повреждением корабля ядра. Эти повреждения, например, могут требовать снижения скорости группы кораблей противника ниже определенного предела. В этом случае в модели требуется учесть следующие состояния системы:

А₁, А₂, А₃ – корабль ядра не поврежден, поражены соответ­ственно ноль, один, два корабля охранения;

А₄, А₅, А₆ – корабль ядра поврежден, поражены соответствен­но ноль, один, два корабля охранения;

А₇ — корабль ядра поражен.

В примере 1 по сравнению с примером 2 состояния А₄, А₅, А₆ объединены в одно состояние А₄. Различие в числе учитываемых состояний определяется различием в целях действия сил.

В примере 3 для сохранения «марковости» процесса введена группа состояний, учитывающих повреждение корабля ядра.

Пример 4. Подводная лодка передает сообщения на команд­ный пункт (КП), осуществляя для повышения надежности пере­дачи сообщения несколько повторных передач радиограммы (РДО) с одним и тем же сообщением.

В процессе передачи сообщения подводная лодка может быть обнаружена и атакована противолодочными силами противника. В этом случае выполнить запланированное число передач РДО подводная лодка может, только оторвавшись от преследования.

Цель использования средств связи подводной лодки – переда­ча на КП сообщения. Цель моделирования – обоснование луч­шего по надежности способа передачи подводной лодкой сообще­ния в условиях противодействия противолодочных сил противника.

В данном случае имеем:

а) Система – подводная лодка и КП.

б) Состояния системы:

А₁ – сообщение на КП не получено; подводная лодка противолодочными силами не поражена;

А₂ – сообщение на КП получено;

А₃ – сообщение на КП не получено; подводная лодка пораже­на противолодочными силами.

в) Шаг системы: передача подводной лодкой РДО. Шаг си­стемы имеет продолжительность, равную математическому ожида­нию промежутка времени между началами двух смежных передач РДО. При этом математическое ожидание времени уклонения под­водной лодки от преследования включается в продолжительность шага.

г) Система способна из состояния А₁ переходить в состоя­ние А₂ или А₃. Из состояний А₂ и А₃ переход ни в какие другие состояния невозможен, так как при этом моделируемый процесс заканчи­вается: в первом случае ввиду достижения цели действий, во вто­ром – из-за поражения подводной лодки. Возможно, что в резуль­тате шага система останется в прежнем состоянии.

Пример 5. Дополнительно к условиям примера 4 следует учесть, что возможность осуществления дальнейших передач РДО непораженной подводной лодкой существенно зависит от того, как подводная лодка пришла в состояние А₁. А именно: если под­водная лодка хотя бы один раз была обнаружена ранее, то против­ник усиливает противолодочную оборону в данном районе, отчего вероятность обнаружения подводной лодки возрастает.

В этом случае следует считать:

а) Система — подводная лодка, КП, противолодочные силы противника.

б) Состояния системы:

А₁ – сообщение на КП не получено, подводная лодка не пора­жена, ранее противником не обнаруживалась; противолодочная оборона в районе не усилена;

А₂ – сообщение на КП не получено, подводная лодка не пора­жена, противником ранее обнаруживалась; противник усилил противолодочную оборону в районе;

А₃ – сообщение на КП получено;

А₄ – сообщение на КП не получено, подводная лодка пораже­на противником.

в) Шаг системы: передача подводной лодкой РДО.

г) Система способна переходить из состояния А₁ или А₂ во все состояния с большим номером. Из состояний А₃ и А₄  переход ни в какие другие состояния невозможен. Данную задачу иллюстрирует граф переходов (рис. 3.4.2), в котором дополнительно к усло­виям задачи принято, что при состоянии системы А₂ противник прини­мает лишь меры, затрудняющие подводной лодке использовать средства радиосвязи).

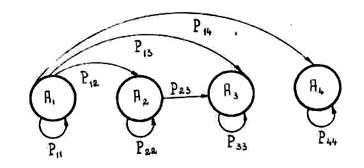
Рис. 3.4.2. Графическое представление модели задачи

Последний пример иллюстрирует следующее правило опреде­ления элементов обстановки, которые должны включаться в поня­тие система:

систему составляют все те элементы обстановки, ко­торые способны изменяться от шага к шагу, изменяя при этом возможность достижения цели действия сил. Элементы обстанов­ки, которые не способны изменяться в результате шага, но влияют на достижение цели действий (например, противолодочные силы противника в примере 4), учитываются при определении вероят­ностей переходов.

Заметим, что в приведенных выше примерах не рассматрива­лись способы определения необходимых вероятностей: поражения объектов противника, обнаружения подводной лодки и т. д. Мы будем счи­тать все необходимые вероятности событий известными.

Оперативно-тактическую постановку задачи осуществляет командир, а интерпретацию процесса как дискретной цепи Маркова должен осуществлять специалист по исследованию операций.

Вряд ли такой специалист будет находиться на корабле, поэтому и интерпретация процесса как дискретной цепи Маркова, и решение задачи должно быть возложено на БИУС. Для этого в БИУС:

- должна иметься достоверная и полная оперативная информация о противнике, а также своих силах и средствах,

- в базах данных БИУС должны храниться априорные вероятности наступления различных событий либо рассчитанные, либо полученные в результате накопления и обработки статистических данных,

- БИУС должна быть интеллектуальной системой, способной «понимать» поставленную командиром задачу и преобразовывать ее в форму, удобную для решения методами теории дискретных цепей Маркова.

Показатели эффективности, вычисляемые методами теории 

дискретных цепей Маркова

Рассматриваемые методы позволяют находить распределение состояний системы на различных шагах процесса. А это открыва­ет возможность с помощью методов теории вероятностей находить различные вероятностные характеристики, используемые в каче­стве показателей эффективности.

Обычно рассматриваемые методы применяются для опре­деления следующих вероятностных характеристик:

– вероятности того, что цель действия сил (своих или против­ника) будет достигнута за заданное число шагов или за заданное время процесса;

– вероятности того, что цель действия сил будет достигнута именно на заданном шаге или именно в заданный момент; 

– математического ожидания числа шагов, необходимых для достижения цели действий;

– математического ожидания времени, необходимого для до­стижения цели действий;

– математического ожидания ущерба, причиняемого против­нику, или ущерба, причиняемого противником нашим силам за заданное число шагов процесса.

И несколько шагов

Основу математической модели цепи Маркова составляют мат­рицы вероятностей переходов системы в возможные состояния за каждый из шагов. В дальнейшем для краткости будем называть их просто матрицами переходов.

Рассмотрим свойства матрицы перехода за один шаг. Обозна­чим через 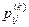 вероятности того, что система, которая перед оче­редным (k-м) шагом была в состоянии А_i, в результате k -го шага перейдет в состояние А_j (i = 1, 2, ... , m; j = 1, 2, ... , m).

Если вероятности переходов 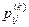меняются от шага к шагу, цепь Маркова называется неоднородной.

Если же вероятности 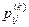одинаковы для всех шагов, цепь Маркова называется однородной. В этом случае вероятности перехода принято обозначать .

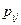Матрица вероятностей переходов за один шаг имеет следующий вид:

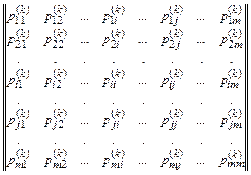
Как видно, матрица вероятностей переходов квадратная, т. е. число строк равняется числу столбцов. Каждый элемент i-й строки матрицы (i = 1, 2, . . . , т) есть вероятность того, что система, которая до k-го шага была в состоянии A_i, после k-го шага перейдет в состоя­ние, номер которого соответствует номеру столбца матрицы.

Например:

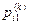– вероятность того, в ре­зультате k-го шага система перейдет из состояния A_i в состояние A₁;

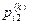– вероятность того, в ре­зультате k-го шага система перейдет из состояния A_i в состояние A₂;

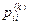– вероятность того, в ре­зультате k-го шага система перейдет из состояния A_i в состояние A_i (т. е. вероятность того, что система останется в состоянии A_i);

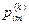– вероятность того, в ре­зультате k-го шага система перейдет из состояния A_i в состояние A_m;

Так как система в результате k-го шага обязательно должна оказаться в одном из т состояний, то сумма вероятностей каждой из строк равняется единице:

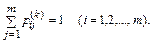
Это свойство часто используется для проверки правильности за­полнения матрицы переходов.

Элементы j-го столбца матрицы переходов (j = 1, 2, ... , т) представляют собой условные вероятности перехода системы в ре­зультате k-го шага в состояния А_j, вычисленные при условии, что перед k-м шагом система находилась в состоянии A_i.

В зависимости от особенностей процесса некоторые из вероят­ностей 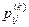 могут быть равны нулю, что означает невозможность перехода системы на k-м шаге из состояния A_i в состояние А_j.

Знание матрицы перехода за один шаг позволяет определить элементы р _ij(п) матрицы переходов за п шагов.

· Через р _ij(п) обозначается вероятность того, что система, бывшая перед первым шагом в состоянии A_i, в результате п шагов (т. е. после п шагов) процесса перейдет в состояние А_j.

Матрица переходов за п шагов определяется в результате по­следовательного матричного перемножения п матриц.

Обозначим через p_k или 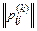 матрицу переходов для k-го ша­га, а через p(п) или  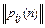– матрицу переходов в результате п шагов.

Символически матричное произведение для неоднородной цепи записывается следующим образом:

p(п)= p₁×p₂×…×p_k×…×p_n

или

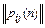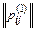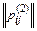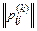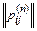                              = × ×…× ×…×             (1)

а для однородной цепи:

p(п)= p₁ⁿ

или

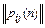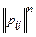                                            =                                         (2)

Смысл же матричного перемножения матриц переходов рас­смотрим на следующем примере.

Пример 6. Пусть заданы матрицы перехода на первом и вто­ром шагах:

Требуется определить матрицу .перехода за два шага

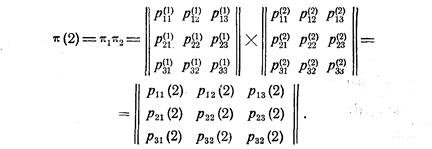
Определим, в качестве примера вероятность р₂₃(2) перехода системы за два шага из второго состояния в третье.

Относительно исходов первого шага системы мы можем только строить гипотезы. А именно, известно, что после первого шага си­стема может из состояния А₂ перейти в состояние A₁ или в состояние А₃, или остаться в состоянии А₂. Известны и вероятности этих гипотез. Ими являются соответственно вероятности , , .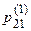

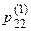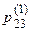Если реализуется гипотеза A₁, то искомое событие (переход системы в состояние А₃) произойдет с условной вероятностью 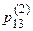, при гипотезе А₂ – с условной вероятностью  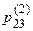и т. д.

Таким образом, можно использовать формулу полной вероят­ности

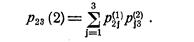
Обратим внимание, что процесс нахождения вероятности 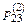 выглядит следующим образом: элементы второй строки матри­цы p₁ почленно умножаются на элементы третьего столбца мат­рицы p₂, затем суммируются найденные произведения.

Аналогичным образом определяются и остальные вероятности матрицы перехода p (2).

В общем виде формула для определения вероятностей перехо­дов системы за два шага имеет вид

(3)

а за п шагов –

(3)

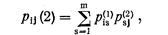
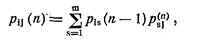
где p_is(п – 1) – вероятность перехода системы из состояния A_i в состояние A_s в результате шагов от первого до (п – 1)-го, или

(4)

(4)

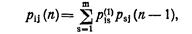
где p_sj (п – 1) – вероятность перехода системы из состояния A_s в состояние A_j в результате шагов от второго до п-го.

Соответственно двум предыдущим выражениям для матрицы p(п) переходов за п шагов справедливы выражения

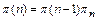                                                                                      (5)

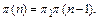                                                                                      (6)

Матрица переходов за п шагов обладает теми же свойствами, что и матрица переходов за один шаг.

Для перемножения матриц переходов на ЭВМ могут быть лег­ко разработаны стандартные процедуры.

Произведение матриц переходов не обладает переместительным свойством. В общем случае p₁ p₂ ¹ p₂ p₁. Это обстоятельство позволяет использовать цепи Маркова для обоснования важного элемента решений командира по поставленным задачам – опреде­ления оптимальной последовательности ударов или, шире, опти­мальной последовательности действий.

Классификация случайных процессов

В большом числе случаев боевые действия сил флота, приме­нение оружия и использование технических средств выступают пе­ред исследователем как случайные процессы, протекающие во времени. Случайными называются такие процессы, которые при их повторении приводят к различным результатам, причем заранее не известно, к каким именно. Случайные процессы изменения со­отношения сил сторон получили название динамики боя [3].

Для количественного, обоснования решений при управлении такими процессами необходимо разрабатывать их математические мо­дели. При разработке математических моделей случайных процес­сов в рассмотрение вводится понятие системы, которая в силу ряда случайных факторов может переходить в различные состояния.

Случайные процессы подразделяются:

· по количеству состояний на процессы со счетным множеством состояний и с несчетным множеством состояний. Примерами случайных процессов с несчетным множеством со­стояний являются процессы изменения подводной лодкой глубины погружения, когда состояние системы – подводной лодки – опре­деляется глубиной погружения; процессы движения по заданной траектории крылатой ракеты, местоположение которой (состояние системы) определяется координатами в трехмерном пространстве. К числу процессов со счетным множеством состояний относят­ся, например, процессы поиска объектов, когда состояния системы отличаются числом обнаруженных объектов; процессы боевых действий, когда состояния системы определяются числом боеспо­собных (или пораженных) объектов.

· по времени смены состояний на процессы с дискретным и непрерывным временем переходов системы из состояния в состояние. Если по соединению кораблей наносится ряд последовательных ударов, то число боеспособных кораблей в составе этого соедине­ния может меняться лишь в моменты нанесения ударов. Это при­мер случайного процесса с дискретным временем переходов. При поиске разведчиками объектов в некотором районе состоя­ние системы – число обнаруженных объектов – может изменить­ся в любой момент времени. Этот процесс является процессом с непрерывным временем переходов.

· по зависимости вероятностей переходов в состояния от текущего времени на стационарные и нестационарные процессы. У стационарных процессов вероятностные характеристики не меняются с течением времени, а у нестационарных являются функцией времени, про­шедшего с начала процесса.

· по зависимости состояния от других состояний на Марковские и не Марковские случайные процессы. Процесс является Марковским, если будущее состояние системы опреде­ляется ее настоящим состоянием и не зависит от того, как именно система пришла в это состояние.

Применение дискретных цепей Маркова

для математического моделирования процессов боевых действий

При обосновании решений командиров по поставленным зада­чам часто возникает необходимость в математических моделях случайных процессов со счетным множеством состояний и дис­кретным или непрерывным временем переходов.

Для моделирования слу­чайных процессов со счетным множеством состояний и с дискретным временем переходов наиболее приемлем аппарат теории дис­кретных цепей Маркова.

Методы математического моделирования многих случайных процессов со счетным множеством состояний и непрерывным временем переходов (стационарных и нестационар­ных, Марковских и не Марковских) рассматриваются в теории мас­сового обслуживания.

Кроме того, существует целый ряд специфических процессов динамики действия сил, таких как процессы поиска и слежения, процессы использования носителей оружия (являющихся также случайными процес­сами со счетным числом состояний, дискретным или непрерывным временем переходов). Для моделирования этих процессов разработаны специальные методы. Очень часто при их разработке использу­ются аппарат или идеи теории дискретных цепей Маркова, теории массового обслуживания, их комбинаций.

Своим названием дискретные цепи Маркова обязаны выдаю­щемуся русскому математику А. А. Маркову, разработавшему ос­новы их теории. Первые его работы в этой области относятся к 1907 г.

Внедрение в практику управления силами электронно-вычисли­тельной техники открыло широкие возможности применения мето­дов теории дискретных цепей Маркова для обоснования решений командиров по поставленным задачам.

Область возможного применения рассматриваемых методов чрезвычайно широка. В большом числе случаев эти методы явля­ются, чуть ли не единственным, эффективным инструментом объективного обоснования решений, когда осуществляется управление некоторой системой, способной изменять свои состояния во времени [3]. Термин система здесь употреблен в широком смысле. Такими системами могут быть технические средства, оружие, корабли, соединения ко­раблей.

Вот некоторые примеры оперативно-тактических ситуаций, ко­гда для эффективного управления необходимо математическое моделирование с использованием методов теории дискретных це­пей Маркова.

1. Артиллерийские и ракетные дуэли кораблей и групп кораб­лей. Целью моделирования при этом может быть:

– обоснование луч­ших способов маневрирования при выходе в позицию применения оружия и в процессе применения оружия,

– лучших способов веде­ния огня,

– прогнозирование возможных тактических приемов про­тивника.

2. Применение по противнику оружия несколькими ударными группами. Возможная цель моделирования:

– обоснование рацио­нальных способов взаимодействия групп,

– определение оптимальной последовательности уда­ров,

– прогнозирование организации противником обороны своих объектов.

3. Организация связи с управляемыми силами, связи взаимо­действия между силами. Цель моделирования:

– обоснование ра­циональной организации связи,

– рациональных способов использо­вания средств связи,

– прогнозирование мероприятий противника по срыву связи.

4. Ведение разведки корабельных соединений и конвоев про­тивника с целью наведения на них ударных сил. Цель моделирования:

– обоснова­ние рациональных способов ведения разведки,

– способов использо­вания разведчиками средств связи,

– прогнозирование способов про­тиводействия противника ведению разведки и наведению ударных сил.

При моделировании процессов боевых действий методы теории цепей Маркова могут применяться как самостоятельно, так и использоваться для разработки блоков моделей.

Прежде чем применять рассматриваемые методы необходимо научиться распознавать в изучаемом процессе черты, присущие дискретным цепям Маркова, и ставить (формулировать) задачу для разработки модели.