Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Для некоторых частных видов матриц перехода можно раз­работать более простые способы определения вероятностей пере­хода р _ij(п) и тем сократить время моделирования. Рассмотрим однородную цепь Маркова, обладающую следую­щими свойствами: система за очередной шаг может из состояния A_i перейти в какие-либо другие состояния, но обратный переход системы из этих состояний в состояние A_i невозможен.

Пронумеруем состояния подобной системы таким образом, что­бы переход системы из состояния с меньшим номером в состояние с большим номером был возможен, а обратный переход невозможен. При этом будем иметь: р _ij > 0, если i £ j; р _ij = 0, если i > j. Матри­ца переходов для такой цепи называется верхней треугольной: все ее элементы, расположенные ниже главной диагонали, равны нулю. Так, для примера 1 при нанесении каждого удара одним и тем же оружием матрица переходов будет иметь следующий вид:

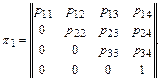
Состояние А₄ называется поглощающим, так как, оказавшись в этом состоянии, система уже не может из него перейти ни в какие другие состояния ни за какое число шагов.

Обратим внимание на следующие обстоятельства, с которыми придется встретиться в дальнейшем.

Во-первых, дискретная цепь может иметь несколько поглощающих состояний. Так, в условиях примера 4 имеются два поглощающих состояния: А₂ (сообщение на КП получено) и А₃ (подводная лодка поражена противником до получения на КП сообщения). Перейдя в одно из этих состоя­ний, система более из них уже не выйдет. Матрица перехода при этом имеет вид

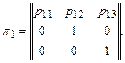
Во-вторых, в качестве поглощающего состояния может выступать группа состояний. Так, если в рамках примера 2 нас будет интересовать вероятность поражения корабля ядра, то группа состояний А₄ – А₆ может быть объединена в одно состояние «корабль ядра поражен», являющееся поглощающим.

Возвратимся к вопросу определения вероятностей р _ij(п) пере­хода системы за п шагов для верхней треугольной матрицы. Непосредственно из свойств верхней треугольной матрицы сле­дует, что

                                           

(7)

                                 (7)

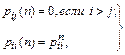
так как, выйдя из состояния A_i, система в него уже никогда не вернется.

Для случая i < j на основании выражений (3), (4) мо­жем записать

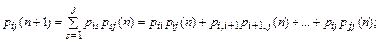(8)

     (8)

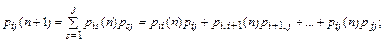(9)

    (9)

Заметим, что суммирование в обоих этих выражениях ведется только от s = i до s = j, так как система не способна переходить в состояния с меньшим номером, поэтому и р _is=0, р _is(п) =0, если s < i;  р _sj = 0, р _sj(п) = 0, если s > j.

Приравняем правые части выражений (8) и (9), опре­делим из полученного равенства

                   

(10)

        (10)

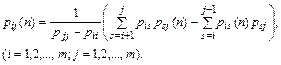
С помощью выражения (10) можно найти зависимости для определения вероятностей переходов из состояния A_i в состояния A_i+1, A_i+2  и т.д.:

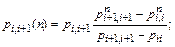(11)

                                                                 (11)

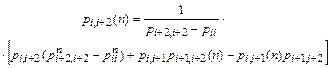(12)

                   (12)

 

и т. д.

В выражении (12) вероятности p_i+1,i+2(n) и p_{i, i+1}(n) определяются с помощью (11). Подобным образом можно оп­ределить все вероятности p_{i , j}(n) при j > i, если p_{i , i}(n)= p_{i , j}(n).

Пример 7. Определение вероятностей p_{i , j}(n) переходов для систем с невосстанавливаемым ущербом.

а) Планируется поражение объекта противника залповым ог­нем корабля. Вероятность поражения объекта за один залп равняет­ся р. Залпы осуществляются в независимых условиях.

Математическая модель должна позволить обосновать число залпов (n), необходимых для поражения объекта. Показателем эффективности является вероятность поражения объекта.

Описанный процесс поражения объекта может быть интерпре­тирован как дискретная цепь с невосстанавливаемым ущербом. Системой является поражаемый объект, способный находиться в двух состояниях: А₁ – не поражен, А₂ – поражен. Шаги процес­са – залпы корабля; моментами шагов являются моменты паде­ния снарядов залпа. Система способна переходить из состояния А₁ в состояние А₂, обратный переход невозможен. Матрица перехода имеет вид

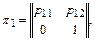
где р₁₁= 1 – р;   р₁₂= р.

Используя (7) и свойства матрицы переходов (сумма элементов строки равна 1), будем иметь

              р₁₁(n) = р₁₁ⁿ; р₁₂(n) = 1 – р₁₁(n) = 1 – р₁₁ⁿ                  (13)

Вероятность поражения объекта в условиях примера составит

W = р₁₂(n) = 1 – (1 – р) ⁿ.

б) В условиях примера «а» следует учесть, что обстреливаемый объект может не только поражаться, но и повреждаться очеред­ными залпами. Вероятность поражения одним залпом неповреж­денного корабля равняется р', поврежденного – р''', вероятность повреждения корабля равна р".

В этом примере система – объект противника – может нахо­диться в одном из трех состояний: А₁ – не поврежден, А₂ – повре­жден, А₃ – поражен.

Система способна переходить из состояния с меньшим номе­ром в состояние с большим номером. Обратные переходы невоз­можны. Матрица перехода имеет вид

,

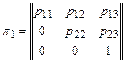где р₁₁ = 1 – р' – р" ; р₁₂ = р" ; р₁₃ = р' ; р₂₂ = 1 – р"' ; р₂₃ = р"'.

Используя (7), получим

                                       р₁₁(n) = р₁₁ⁿ; р₂₂(n) = р₂₂ⁿ                              (14)

На основании (11) можем записать

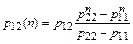                                                                         (15)

Для определения р₁₃(n), р₂₃(n) используем свойства матрицы переходов (сумма элементов строки равна 1):   

          р₁₃(n) = 1– р₁₁(n) – р₁₂(n); р₂₃(n) = 1– р₂₂(n).              (16)

Показатель эффективности в рассматриваемом примере W = р₁₃(n), если процесс начинается из состояния А₁. Методы определения показателей эффективности на основании матриц переходов будут рассмотрены позже.

в) Планируется разведка соединения кораблей противника подводной лодкой, осуществляемая в следующих условиях. Раз­ведка ведется циклично. Установив контакт с целью, подводная лодка определяет элементы ее движения, после чего всплывает для передачи донесения на КП. Всплытие на связь может приве­сти к потере контакта и вызвать необходимость его восстановле­ния. Затем цикл повторяется. Если противник обнаружит радио­передачу подводной лодки, он примет меры, которые затруднят подводной лодке в последующие циклы поддержание контакта с целью. Если же подводная лодка будет обнаружена противолодоч­ными силами, она подвергнется атаке и сможет продолжить раз­ведку только после уклонения. В последующие циклы подводная лодка будет действовать в условиях усиленного состава сил про­тиволодочной обороны противника и проведения им мероприятий по отрыву от преследования.

Цель действий подводной лодки – передача контакта ударным силам на заданном рубеже (после n циклов) при установленной продолжительности цикла.

Математическая модель должна позволить оценить влияние скрытности подводной лодки на эффективность выполнения по­ставленной задачи.

Показателем эффективности в данном случае является вероят­ность того, что на п-м цикле разведки подводная лодка будет иметь контакт с целью. Для определения этого показателя необ­ходимо рассмотреть однородную цепь Маркова, в которой систему составляют соединение противника с силами и средствами ПЛО и подводная лодка-разведчик.

Состояниями системы являются: А₁ – контакт с целью имеется, подводная лодка и ее радиопередачи противником ранее не обна­руживались; А₂ – контакт с целью имеется, противник ранее обна­руживал радиопередачу подводной лодки; А₃ – контакт с целью имеется, противник ранее обнаруживал саму подводную лодку; А₄ – потерян контакт или поражена подводная лодка.

Шаг системы – очередной цикл ведения разведки. Система за один шаг мо­жет переходить из состояния с меньшим номером в одно из со­стояний, имеющих больший номер, либо же оставаться в прежнем со­стоянии.

Параметры, характеризующие процесс разведки, приведены в таблице 1.

Вероятности Р _ij перехода за один шаг равны:

р₁₁ = g₁(1 – р_об1)(1 – s₁); р₁₂ = g₁(1 – р_об1)s₁; р₁₃ = g₁р_об1(1 – w₁); 

 р₁₄ = р_об1w₁ + (1 – р_об1w₁)( 1 – g₁);

р₂₂ = g₂(1 – р_об1); р₂₃ = g₂ р_об1(1 – w₁); р₂₄ = р_об1w₁(1 – w₁) + (1 – р_об1w₁)(1 – g₂);

р₃₃ = g₂(1 – р_об2w₂); р₃₄ = р_об2w₂ + (1 – р_об2w₂)( 1 – g₂);

 

Таблица 1

Наименование параметра	Условия разведки
	пл противником не обнаружена	Противник обнаружил радиопередачу пл	Противник обнаружил пл
Вероятность установления подводной лодкой контакта с целью после очередного всплытия на связь	g1	g2	g3
Вероятность обнаружения противником радиопередач подводной лодки	s1	s2	s2
Вероятность обнаружения подводной лодки противолодочными силами противника	Pоб1	Pоб1	Pоб2
Вероятность поражения противником обнаруженной подводной лодки	w1	w2	w2

 

Для нахождения распределения состояний системы использу­ем формулы (7), (11), (12). Будем иметь

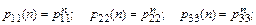(17)

                                        (17)

(19)

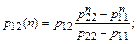(18)

                                                                            (18)

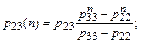                                                                           (19)

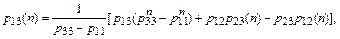(20)

               (20)

где р₁₂(n) и р₂₃(n) определяются по формулам (18), (19);

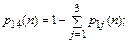
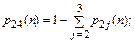
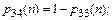(21)

   (21)

Показателем эффективности в данном случае является величи­на W = 1 – р₁₄(n), если процесс начинается из состояния А₁.

Заканчивая на этом рассмотрение примеров цепей с невосста­навливаемым ущербом, заметим, что с помощью формул (7), (10) можно находить вероятности р _{i , i+l}(п) при различных зна­чениях l.

Для вычислений по этим формулам разрабатываются стан­дартные процедуры. Разумеется, что и для систем с невосстанавливаемым ущербом вероятности переходов р _{i , j}(п) могут быть по­лучены путем перемножения матриц.