Дискретное распределение считается теоретически заданным, если известны все возможные значения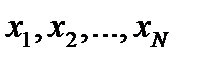 
, принимаемые величиной, и вероятности 
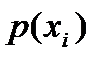для каждого события в поле испытаний. Так как эти события должны образовывать полную группу, то полная вероятность
 .
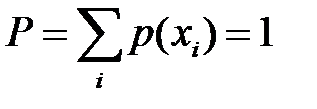| (2-1.10) |
При дискретном распределении общая масса вероятности, равная единице, сосредоточена в счетной или конечной системе точек х i . Другими словами, точечное распределение массы вероятности подобно, например, точечному распределению электрических зарядов. К теоретическим распределениям дискретных величин относятся биномиальное, гипергеометрическое, распределение Пуассона. Каждое из этих распределений описывается аналитической функцией, выражающей зависимость вероятности от дискретной переменной величины и параметров распределения.
Функция биноминального распределения:
 ,
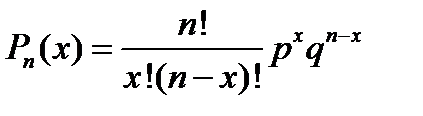| (2-1.11) |
где q = 1 – p, n, p - параметры распределения.
Функция распределения Пуассона
 ,
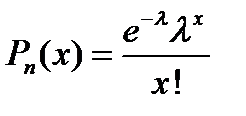| (2-1.12) |
где l – параметр распределения.
Для теоретического изучения распределения непрерывных величин вводится понятие плотности вероятности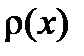 
 ,
|
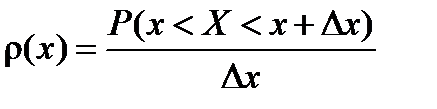где Dx длина малого интервала, начинающегося в точке x.
Для бесконечно малого интервала Dx вероятность
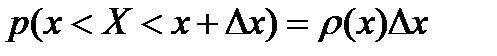, (2-1.13)
для конечного интервала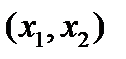 
, где 
,
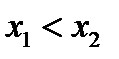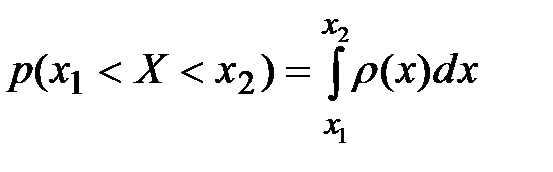
Интеграл от плотности вероятности распределения по любому промежутку оси дает вероятность попадания величины X в этот промежуток Dx.
Плотностью распределения может служить любая интегрируемая функция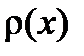 
, удовлетворяющая двум условиям:
1.  .
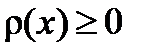| (2-1.14) |
2.  .
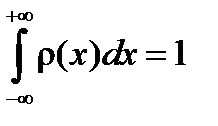| (2-1.15) |
Вероятность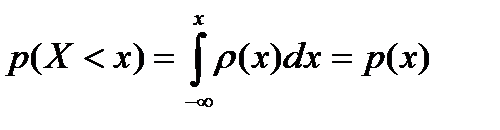 
(2-1.16) называется интегральной функцией распределения, в отличие от плотности вероятности 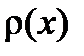, которую называют дифференциальной функцией распределения.
Графическое представление дифференциальной функции распределения
|
|
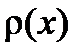
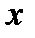
| P(x) |
|
|
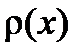
| Рис. 2-1.5. Плотность вероятности |
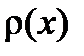является ординатой кривой распределения, а вероятность Р(х) равна площади под этой кривой oт -¥ до x. По определению Р( x ) обладает следующими свойствами:
1. P(x) – непрерывная возрастающая функция: её
приращение в промежутке 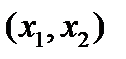равно вероятности для величины X попасть в этот промежуток. В самом деле, по правилу сложения вероятностей:
,
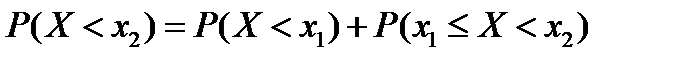т.е.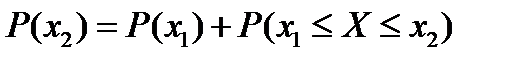 
,
и следовательно,
.
 ,
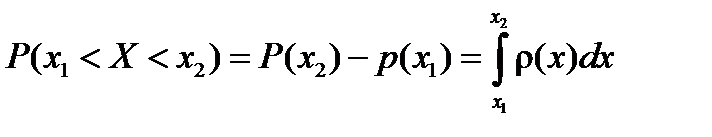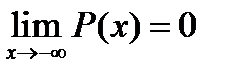| (2-1.17) |
 .
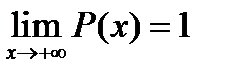| (2-1.18) |
2. Производная от интегральной функции распределенная P(x) равна плотности 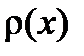, т.е
 .
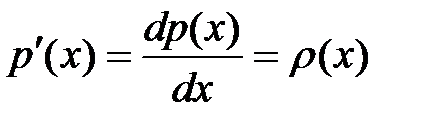| (2-1.19) |
Параметры теоретического распределения.
Математическое ожидание.
Среднее арифметическое, являющееся центром эмпирического распределения, переходит в математическое ожидание M ( x ) при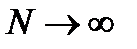 
. В теоретическом распределении дискретных величин математическое ожидание
 .
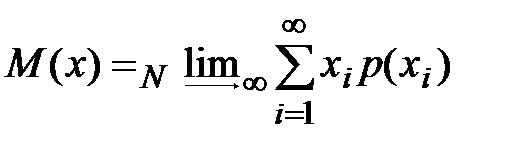| (2-1.20) |
Математическое ожидание непрерывно распределенной величины
 .
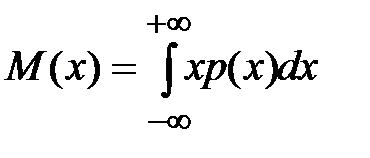| (2-1.21) |
При многократных экспериментальных определениях некоторой величины в одних и тех же условиях (при отсутствии систематических погрешностей) математическое ожидание можно рассматривать как "истинное" значение этой величины.
Дисперсия
В теоретическом распределении дисперсия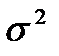 
есть математическое ожидание квадрата отклонений случайной величины от её математического ожидания
 .
| (2-1.22) |
Если обозначить M(x) = a, то дисперсия распределения дискретной величины может быть записана как
 ,
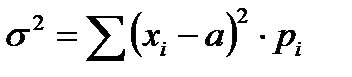| (2-1.23) |
в случае непрерывной величины как
 .
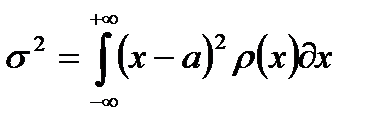| (2-1.24) |
Дата: 2019-03-05, просмотров: 357.
