Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Кинетическая энергия притяжения может быть только положительной, потенциальная энергия между молекулами отрицательна. Если кинетическая энергия велика, так что сумма кинетической и потенциальной энергий рассматриваемой системы молекул положительна, то молекулы, представленные самим себе, стремятся разойтись на бесконечно большое расстояние. Такое состояние системы – газ, и он стремится к расширению.

При сжатии газа его плотность увеличивается и среднее расстояние между молекулами уменьшается. При этом, как видно из формулы (2-2.1), уменьшается потенциальная энергия. Если средняя кинетическая энергия молекул не слишком велика, то наступает такой момент, когда сумма кинетической и потенциальной энергий будет отрицательной. Такая система молекул уже не может самопроизвольно рассеяться в большем объеме, поскольку после рассеяния ее энергия состояла бы лишь из кинетической, т. е. была бы положительной, что невозможно, так как полная энергия системы отрицательна. Вспомните из механики: энергия связанного состояния отрицательна. Молекулы удерживаются друг около друга в конечном объеме. Такое состояние системы молекул является либо жидким, либо твердым. Чаще всего при сжатии газа образуется жидкое состояние.

Этот процесс образования жидкости при сжатии газа может иметь место лишь в случае, если кинетическая энергия молекул, т. е. температура, не очень велика.

Поверхностное натяжение

Рис. 3

Рис. 2-2.3. Силы на границе жидкость - пар

Итак, мы пришли к выводу, что жидкое состояние возникает тогда, когда кинетическая энергия мала, а потенциальная энергия притяжения молекул превосходит по абсолютному значению кинетическую энергию. Силы притяжения между молекулами жидкости значительны и обеспечивают удержание молекул в объеме жидкости. Таким образом, у жидкости образуется поверхность, которая ограничивает ее объем. Площадь поверхности, ограничивающей данный объем, зависит от формы. Из геометрии известно, что при заданном объеме минимальной поверхностью обладает шар.

Поверхность жидкости, соприкасающейся с другой средой (стенки сосуда, ее собственный пар, твердое тело), находится в особых условиях по сравнению с остальной массой жидкости. Возникают эти особые условия потому, что молекулы пограничного слоя жидкости, в отличие от молекул в ее глубине, окружены молекулами той же жидкости не со всех сторон.

Часть “соседей” поверхностных молекул – это частицы второй среды, с которой жидкость граничит. Эта среда может отличаться от жидкости как природой, так и плотностью частиц.

В случае, если жидкость граничит со своим собственным паром (насыщенным), т. е. в случае, когда мы имеем дело с одним веществом, сила, направлена внутрь жидкости (рис. 2-2.3). Это объясняется тем, что плотность молекул в жидкости много больше, чем в насыщенном паре над жидкостью (вдали от критической температуры), и поэтому сила притяжения, испытываемая молекулой поверхностного слоя со стороны молекул жидкости, больше, чем со стороны молекул пара.

Отсюда следует, что при увеличении поверхности жидкости некоторое число молекул из объема жидкости должно быть поднято в поверхностный слой. Для этого необходимо произвести внешнюю работу. Если при постоянной температуре обратимым путем изменить поверхность жидкости на бесконечно малую величину dS, то необходимая для этого работа

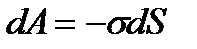.                                       (2-2.2)

Знак минус указывает на то, что увеличение поверхности (dS > 0) сопровождается отрицательной (затраченной) работой.

Коэффициент 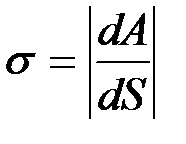 является основной величиной, характеризующей свойства поверхности жидкости, и называется коэффициентом поверхностного натяжения. Следовательно, коэффициент поверхностного натяжения измеряется работой, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.

С другой стороны, из термодинамики известно, что при изотермических процессах роль потенциальной энергии играет свободная энергия, для которой справедливо соотношение dF = -dA, где dA – работа, связанная с возникновением свободной энергии dF (свободной энергией системы называется та ее часть, которая может быть превращена в работу). В результате однородности поверхности очевидно, что свободная энергия пропорциональна площади поверхности.

На основании сказанного выше с учетом (2-2.2) можно написать:

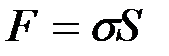,                                               (2-2.3)

т. е. коэффициент поверхностного натяжения жидкости можно определить как свободную энергию жидкости, приходящуюся на единицу ее поверхности. В системе СИ s имеет размерность Дж/м² или Н/м. Поверхностное натяжение зависит от свойств жидкости и изменяется в широких пределах. Например, при 20⁰С для воды s = 0,073 Н/м, для ртути s = 0,465 Н/м.