Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Закон распределения можно представить в виде таблицы:

x i

vi

Более наглядно закон распределения представляется графически.

Среди многих способов графического изображения распределения чаще всего применяются два способа: построение полигона частот (рис. 2-1. 1, б) и построение гистограммы (рис. 2-1. 1, а). В первом случае значения, лежащие в данном интервале, "стягиваются" к середине этого интервала, т. е. условно считают, что все варианты любого интервала имеют величину, соответствующую его середине. На гистограмме (рис. 2-1. 1, а) каждый интервал изображается прямоугольником с шириной, пропорциональной ширине интервала, и с высотой, пропорциональной частоте данного интервала. Изображение распределения с помощью гистограммы представляет собой другой крайний случай идеализации: все значения частот, лежащие внутри ин

а

б

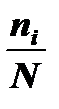
Рис.2-1. 1. Графическое изображение распределения: а – гистограмма, б – полигон

тервала, считаются распределенными равномерно по всему интервалу. Поэтому в принципиальном отношении оба способа отображения следует считать равноценными, и выбор между ними определяется привычкой исследователя.

Параметры распределения

Главным орудием статистики являются обобщающие показатели, основанные на данных массового наблюдения. Важнейшими из обобщающих показателей массового процесса являются средние величины. В достаточно большом числе наблюдений среднее 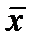 отражает типичные черты массового процесса. Среднее – это тот центр, около которого группируются отдельные значения наблюдаемых и изучаемых элементов массового процесса. В практике работы научно-исследовательских лабораторий из многих видов средних, которые известны в общей теории статистики, чаще всего применяется среднее арифметическое. Среднее арифметическое есть частное от деления суммы значений признака на число элементов совокупности.

Среднее арифметическое обладает рядом математических свойств.

1. Среднее арифметическое суммы равно сумме средних арифметических.

2. Если одно из слагаемых – постоянная величина, то среднее арифметическое суммы равно сумме средних арифметических плюс постоянная величина.

3. Постоянный множитель или делитель можно вынести за знак среднего.

4. Алгебраическая сумма отклонений – 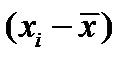 равна нулю.

5. Сумма квадратов отклонений от среднего арифметического меньше, чем сумма квадратов отклонений от любого другого числа а:

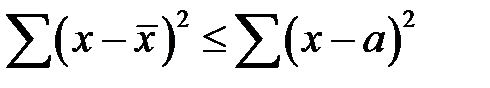^.                                                         (2-1.5)

6. Среднее может быть получено как сумма произведений вариант на их частости

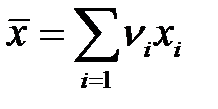 – взвешенное среднее ,               (2-1.6)

 Среднее квадратичное отклонение, дисперсия и их свойства

В качестве показателя размера вариации вариант в статистике принято среднее квадратичное отклонение S. Для его вычисления все отклонения возводятся в квадрат, потом вычисляется среднее из полученных квадратов – средний квадрат отклонений, а затем из этого среднего извлекают корень. В экспериментальных распределениях при определении среднего квадрата квадраты отклонений делятся на (N-1)

.

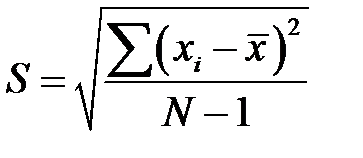(2-1.7)

Дисперсия распределения D:

.

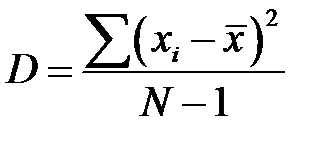(2-1.8)

Формулу дисперсии (2-1.8) легко представить в другом виде, более удобном для вычисления: .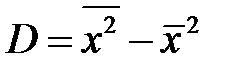

Свойства дисперсии и среднего квадратичного отклонения:

1. Если все значения вариант увеличить на одну и ту же величину а, то на ту же величину а увеличивается их среднее арифметическое. Отклонения же останутся без изменения. Значит, останутся без изменения дисперсия и среднее квадратичное отклонение.

2. Если все значения вариант умножить на одно и то же число К, то в К раз увеличится их среднее арифметическое , отклонения от среднего арифметического 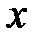- и среднее квадратичное отклонение S (дисперсия) увеличится в К² раз.

3. Средняя величина квадратов отклонений вариант от любой величины а, больше дисперсии D_. на квадрат отклонения этой величины а от среднего арифметического вариант.

4. Если совокупность разбита на несколько частей, то общая дисперсия является суммой средней величины дисперсии внутри отдельных частей совокупности D_i и среднего квадрата отклонения частных средних от общей средней 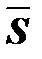²

(11)

^.

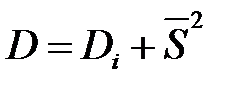Мода

Важным показателем характеристики распределения является мода. Мода – это наиболее часто встречающееся значение варианты. Мода – это значение варианты, которой соответствует наибольшая относительная частота.

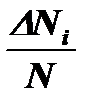
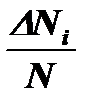
Рис. 2-1.2. Положительная асимметрия             Рис. 2-1.3. Отрицательная                                                                                                                                                                                                                                                                             асимметрия

Асимметрия и эксцесс

Гистограммы распределений изучаемых статистических совокупностей довольно часто бывают асимметричными (рис. 2-1.2, 2-1.3), Если среднее арифметическое лежит правее моды, то асимметрия положительная, если левее моды – отрицательная. Для статистической оценки распределения необходимо вычислять меру асимметрии, называемую коэффициентом асимметрии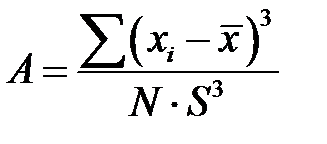

 вычисления. В основу коэффициента асимметрии положено среднеквадратичное отклонение, которое даёт возможность более полно учесть крайние значения вариант. При наличии асимметрии одна сторона кривой дает большее кубическое отклонение, чем другая, и так как знак при кубическом отклонении сохраняется, то разница между суммами кубических отклонений показывает положительную либо отрицательную асимметрии.

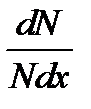
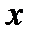
a

б

в

Рис.2-1.4. Распределения с разными показателями эксцесса

Наряду с асимметрией при статистическом анализе рядов распределения важное значение имеет мера эксцесса. Мера эксцесса – это показатель отличия данного распределения от нормального по концентрации вариант около центра распределения. Вычисление этого показателя делается для того, чтобы определить, насколько кривая, полученная из опыта, оказывается более плоской и растянутой, или, наоборот, более сжатой и выпуклой в центре по сравнению с кривой нормального распределения.

Показатель эксцесса выражается следующей формулой:

^.

Если Е > 1 , то эксцесс положительный и вершина кривой будет выше нормальной, и наоборот, если Е < 1 , то эксцесс отрицательный, вершина кривой ниже нормальной (рис. 2-1.4).

Теоретическое распределение

Теоретическое распределение – это математическая модель распределения вероятности по значениям дискретной случайной величины или по интервалам непрерывной случайной величины.

Вероятность

В эмпирическом распределении относительное число попаданий в заданный интервал дается частостью 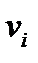, в теоретическом распределении подобная величина называется вероятностью. Вероятность есть мера объективной возможности данного события. Вероятность связана с частостью появления переменной величины:

.

(2-1.9)

Вероятность выражает вполне определенную, хотя и своеобразную, связь между постоянным комплексом условий и случайным событием в поле испытаний, количественно характеризуя единство необходимого и случайного. Конкретный смысл вероятности заключается в том, что она определяет среднюю частость, с которой можно ожидать появления события в длинных сериях испытаний. Значение вероятности изменяется в пределах от нуля до единицы.