Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Теперь ясно, в чем заключаются указанные выше особые условия, в которых находится поверхность жидкости. Они заключаются в том, что поверхность жидкости обладает избыточной по сравнению с остальной массой жидкости потенциальной (свободной) энергией.

К чему же это приводит? Так же, как в механике, система стремится достигнуть состояния с наименьшей потенциальной энергией, и только состояние с наименьшей потенциальной энергией является устойчивым, в термодинамике система в изотермических условиях стремится достигнуть состояния с наименьшей потенциальной энергией. Поэтому поверхность жидкости стремится сократиться. Благодаря этому вдоль поверхности жидкости по касательной к ней действуют силы, называемые силами поверхностного натяжения. В этом отношении жидкость уподобляется тонкой резиновой пленке, растянутой изотропно по всем направлениям в плоскости поверхности, которой окружен объем жидкости. Наличие поверхностного натяжения очень эффектно демонстрируется с помощью мыльных пленок.

Р

В

А

Рис. 2-2.4. Проволочная рамка с мыльной пленкой

Если, например, опустить проволочную рамку, одна из сторон которой АБ подвижна (рис. 2-2.4), в мыльный раствор, то вся она затянется пленкой жидкости. Силы поверхностного натяжения принуждают пленку сокращаться, и подвешенная перекладина АВ вслед за пленкой перемещается вверх. Чтобы сохранить ее в равновесии, к перекладине нужно приложить силу Р в виде груза (сюда входит и вес самой перекладины).

Поверхностная сила f с учетом того, что пленка имеет две поверхности (пленка представляет собой слой жидкости), равна при равновесии весу груза Р:

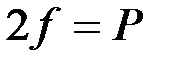и  .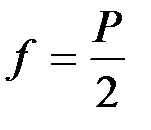

Если под действием силы перекладина, увлекаемая пленкой, переместилась на расстояние dh из положения АВ, то работа, совершенная силой f, равна 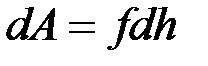. Работа эта равна уменьшению свободной энергии пленки dF, которое, как мы знаем, равно 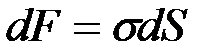. В данном случае 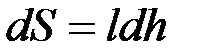, где l – длина рамки. Отсюда  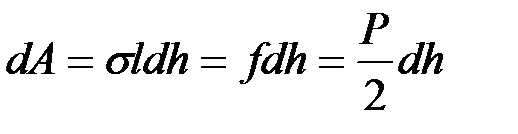и

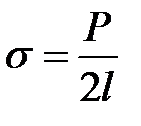  .                                           (2-2.4)

Из (2-2.4) следует, что коэффициент поверхностного натяжения может быть определен как величина, равная силе поверхностного натяжения, действующего на единицу длины линии, являющейся границей жидкости, т. е.

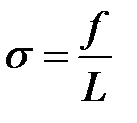 .                                      (2-2.5)

Сила f направлена перпендикулярно к любому элементу длины L, разграничивающей поверхность жидкости, и является касательной к ее поверхности.

Чтобы понять, как возникают силы поверхностного натяжения, действующие вдоль поверхности, необходимо принять во внимание, что кроме сил притяжения на молекулы поверхностного слоя действуют также и другие силы, которые не позволяют этим молекулам переместиться внутрь жидкости, т. е. силы со стороны молекул внутреннего слоя. Вблизи же поверхности имеет место динамическое равновесие: число молекул, выходящих на поверхность каждую секунду из внутренних областей, равно числу молекул, уходящих каждую секунду из поверхностного слоя во внутренние области.

Динамическое равновесие возможно лишь при условии, что плотность молекул в поверхностном слое меньше, чем внутри жидкости. Поясним это утверждение следующим рассуждением. Для того чтобы перейти из внутренних слоев в поверхностный, молекуле необходимо “раздвинуть” молекулы поверхностного слоя и преодолеть силы притяжения со стороны молекул внутренних слоев, стремящихся удержать ее там.

fн

fр

fр

fн

Рис. 2-2.5. Блоки с нитью

Чтобы перейти из поверхностного слоя во внутренний (вниз), молекуле надо лишь “раздвинуть” молекулы внутреннего слоя. Таким образом, молекуле легче перейти из поверхностного слоя во внутренний, чем наоборот. Поэтому говорят, что поверхностный слой находится как бы в растянутом состоянии. Толщина поверхностного слоя составляет несколько молекулярных слоев.

Возникновение сил поверхностного натяжения удобно представить по аналогии со схемой сил, представленных на рис. 2-2.5

Через закрепленные блоки перекинута нить, на которой в вертикальном направлении действует равнодействующая сила f_р , а в горизонтальном направлении в нити действует сила натяжения f _н.

Поверхностное натяжение зависит от свойств вещества, с которым соприкасается поверхность жидкости. Поэтому, когда идет разговор о поверхностном натяжении, надо указывать не только жидкость, которая имеется в виду, но и вещество, с которым поверхность жидкости соприкасается, т. е. коэффициент должен быть снабжен двумя индексами, указывающими две граничащие между собой среды, например, s₁₂ – твердое тело – жидкость.

Капиллярные явления

h

стекло

R=r

h

вода

ртуть

Рис. 2-2.6. Жидкости в капиллярах

Известно, что в узких стеклянных трубках–капиллярах, опущенных в жидкость, жидкость поднимается на некоторую высоту (рис. 2-2.6). Причиной этому является поверхностное натяжение.

Рассмотрим поверхность жидкости, опирающуюся на некоторый плоский контур. Если поверхность жидкости не плоская, то стремление ее к сокращению под действием сил поверхностного натяжения приведет к возникновению давления, дополнительно к тому, которое испытывает жидкость с плоской поверхностью. В случае выпуклой поверхности это

Р0

Р0+DР

Р0-DР

Рис. 2-2.7. Силы поверхностного натяжения

давление положительно (рис. 2-2.7), в случае вогнутой – отрицательно (в последнем случае поверхностный слой, стремясь сократиться, растягивает жидкость). Величина добавочного давления DР должна, очевидно, возрастать с увеличением коэффициента поверхностного натяжения и кривизны поверхности.

Величина добавочного давления над произвольной поверхностью вычисляется по формуле Лапласа:

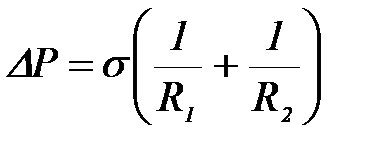.        (2-2.6)

Здесь R₁ и R₂ – радиусы кривизны поверхностного слоя, величина 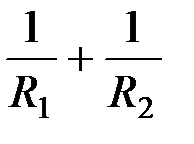 называется средней кривизной произвольной поверхности в данной точке. Если поверхность сферическая, то R₁ = R₂ и

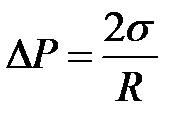,                                     (2-2.7)

где R – радиус сферы. Добавочное давление D Р (иногда его называют лапласовым давлением) обусловливает изменение уровня жидкости в капиллярных трубках. Поэтому его еще называют капиллярным давлением.

Если жидкость полностью смачивает стенки капилляра, то поверхность ее имеет вогнутую форму ( D Р < 0), если полностью не смачивает – выпуклую ( D P > 0). Поэтому в случае смачивания капилляра уровень жидкости в нем будет выше, чем с сосуде при не смачивании (рис. 2-2.6). Жидкость поднимается или опускается в капилляре до тех пор, пока добавочное давление D Р не сравняется с гидростатическим давлением поднявшегося или опустившегося столба жидкости. Если считать, что жидкость полностью смачивает поверхность капилляра, то радиус кривизны мениска R совпадает с внутренним радиусом трубки r. По равенству лапласова и гидростатического давления можно записать:

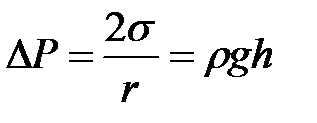,                                    (2-2.8)

 где r – плотность жидкости, h – высота ее поднятия, g – ускорение силы тяжести.

Из равенства (2-2.8) можно определить коэффициент поверхностного натяжения:

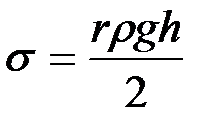 .                                (2-2.9)

Формула (9) используется в качестве рабочей при определении коэффициента поверхностного натяжения капиллярным методом.

Экспериментальная часть