Лабораторных работ
Издательство
Национального исследовательского
Иркутского государственного технического университета
2011
Физика. Молекулярная физика: методические рекомендации к выполнению лабораторных работ. / Сост.: А.Д. Афанасьев, Л.В. Днепровская, М.Я. Яраева Иркутск: Изд-во ИрГТУ, 2011. 92с.
Соответствует содержанию разделов государственных стандартов по направлениям 090900 Информационная безопасность, 210400 Радиотехника, 222900 Наноматериалы и микросистемная техника, 210700 Инфокоммуникационные технологии и системы связи. Содержат описания 8 лабораторных работ по курсу физики (раздел «Молекулярная физика»).
Предназначены для студентов 1 курса специальностям 090900 Информационная безопасность, 210400 Радиотехника, 222900 Наноматериалы и микросистемная техника, 210700 Инфокоммуникационные технологии и системы связи Физико-технического института Национального исследовательского Иркутского государственного технического университета
Библиогр. назв., иллюстр. 42, табл. 17
| Лабораторная работа 2-1. Изучение статистического распределения частоты электрических сигналов………………………………………... | 4 |
| Лабораторная работа 2-2. Молекулярное строение жидкостей и методы определения коэффициента поверхностного натяжения………………. | 19 |
| 2-2.1. Определение коэффициента поверхностного натяжения методом сравнения…………………………………………………………………… | 26 |
| 2-2.2. Определение коэффициента поверхностного натяжения методом компенсации разности давлений поверхностного слоя жидкости (метод Штейна)……………………………………………………………………. | 27 |
| 2-2.3. Определение коэффициента поверхностного натяжения жидкости методом отрыва кольца…………………………………………………… | 28 |
| 2-2.4. Определение коэффициента поверхностного натяжения жидкости методом отрыва капель……………………………………………………. | 30 |
| Лабораторная работа 2-3. Определение средней длины свободного пробега и эффективного диаметра молекул газа………………………… | 33 |
| Лабораторная работа 2-4. Определение коэффициента вязкости жидкости……………………………………………………………………. | 41 |
| 2-4.1. Метод вискозиметрии………………………………………………. | 47 |
| 2-4.2. Метод Стокса………………………………………………………... | 49 |
| Лабораторная работа 2-5. Изучение фазовых переходов первого рода. | 53 |
| Лабораторная работа 2-6. Определение отношения удельных теплоемкостей воздуха……………………………………………………… | 60 |
| Лабораторная работа 2-7. Теплоемкость твердых тел и ее определение методом охлаждения………………………………………………………... | 69 |
| Лабораторная работа 2-8. Теплопроводность газов…………………….. | 80 |
| Приложение 1………………………………………………………………. | 87 |
| Приложение 2……………………………………………………………...... | 88 |
Лабораторная работа 2-1
Изучение статистического распределения частоты электрических сигналов
Цель работы: Ознакомиться со статистическими закономерностями физических величин
Задача работы: Провести статистическое исследование эмпирической совокупности частоты электрических сигналов, регистрируемых от сети пересчетным прибором.
Теоретическая часть
Представление экспериментального закона распределения
Закон распределения можно представить в виде таблицы:
| x i | ||||||||||||||
| vi |
Более наглядно закон распределения представляется графически.
Среди многих способов графического изображения распределения чаще всего применяются два способа: построение полигона частот (рис. 2-1. 1, б) и построение гистограммы (рис. 2-1. 1, а). В первом случае значения, лежащие в данном интервале, "стягиваются" к середине этого интервала, т. е. условно считают, что все варианты любого интервала имеют величину, соответствующую его середине. На гистограмме (рис. 2-1. 1, а) каждый интервал изображается прямоугольником с шириной, пропорциональной ширине интервала, и с высотой, пропорциональной частоте данного интервала. Изображение распределения с помощью гистограммы представляет собой другой крайний случай идеализации: все значения частот, лежащие внутри ин
| а |
| б |
|
| Рис.2-1. 1. Графическое изображение распределения: а – гистограмма, б – полигон |
Параметры распределения
Главным орудием статистики являются обобщающие показатели, основанные на данных массового наблюдения. Важнейшими из обобщающих показателей массового процесса являются средние величины. В достаточно большом числе наблюдений среднее 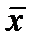 отражает типичные черты массового процесса. Среднее – это тот центр, около которого группируются отдельные значения наблюдаемых и изучаемых элементов массового процесса. В практике работы научно-исследовательских лабораторий из многих видов средних, которые известны в общей теории статистики, чаще всего применяется среднее арифметическое. Среднее арифметическое есть частное от деления суммы значений признака на число элементов совокупности.
отражает типичные черты массового процесса. Среднее – это тот центр, около которого группируются отдельные значения наблюдаемых и изучаемых элементов массового процесса. В практике работы научно-исследовательских лабораторий из многих видов средних, которые известны в общей теории статистики, чаще всего применяется среднее арифметическое. Среднее арифметическое есть частное от деления суммы значений признака на число элементов совокупности.
Среднее арифметическое обладает рядом математических свойств.
1. Среднее арифметическое суммы равно сумме средних арифметических.
2. Если одно из слагаемых – постоянная величина, то среднее арифметическое суммы равно сумме средних арифметических плюс постоянная величина.
3. Постоянный множитель или делитель можно вынести за знак среднего.
4. Алгебраическая сумма отклонений – 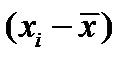 равна нулю.
равна нулю.
5. Сумма квадратов отклонений от среднего арифметического меньше, чем сумма квадратов отклонений от любого другого числа а:
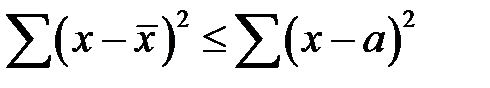 . (2-1.5)
. (2-1.5)
6. Среднее может быть получено как сумма произведений вариант на их частости
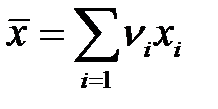 – взвешенное среднее , (2-1.6)
– взвешенное среднее , (2-1.6)
Среднее квадратичное отклонение, дисперсия и их свойства
В качестве показателя размера вариации вариант в статистике принято среднее квадратичное отклонение S. Для его вычисления все отклонения возводятся в квадрат, потом вычисляется среднее из полученных квадратов – средний квадрат отклонений, а затем из этого среднего извлекают корень. В экспериментальных распределениях при определении среднего квадрата квадраты отклонений делятся на (N-1)
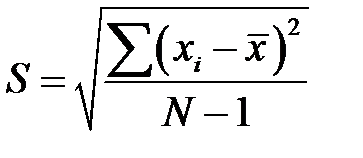 . .
| (2-1.7) |
Дисперсия распределения D:
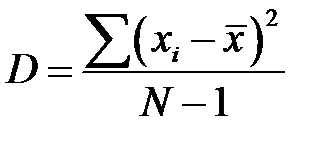 . .
| (2-1.8) |
Формулу дисперсии (2-1.8) легко представить в другом виде, более удобном для вычисления: 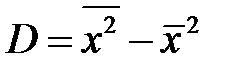 .
.
Свойства дисперсии и среднего квадратичного отклонения:
1. Если все значения вариант увеличить на одну и ту же величину а, то на ту же величину а увеличивается их среднее арифметическое. Отклонения же останутся без изменения. Значит, останутся без изменения дисперсия и среднее квадратичное отклонение.
2. Если все значения вариант умножить на одно и то же число К, то в К раз увеличится их среднее арифметическое  , отклонения от среднего арифметического
, отклонения от среднего арифметического 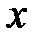 -
-  и среднее квадратичное отклонение S (дисперсия) увеличится в К2 раз.
и среднее квадратичное отклонение S (дисперсия) увеличится в К2 раз.
3. Средняя величина квадратов отклонений вариант от любой величины а, больше дисперсии D. на квадрат отклонения этой величины а от среднего арифметического вариант.
4. Если совокупность разбита на несколько частей, то общая дисперсия является суммой средней величины дисперсии внутри отдельных частей совокупности Di и среднего квадрата отклонения частных средних от общей средней 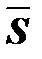 2
2
| (11) |
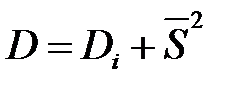 .
.
Мода
Важным показателем характеристики распределения является мода. Мода – это наиболее часто встречающееся значение варианты. Мода – это значение варианты, которой соответствует наибольшая относительная частота.
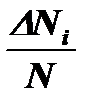
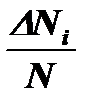
Рис. 2-1.2. Положительная асимметрия Рис. 2-1.3. Отрицательная
асимметрия
Асимметрия и эксцесс
Гистограммы распределений изучаемых статистических совокупностей довольно часто бывают асимметричными (рис. 2-1.2, 2-1.3), Если среднее арифметическое лежит правее моды, то асимметрия положительная, если левее моды – отрицательная. Для статистической оценки распределения необходимо вычислять меру асимметрии, называемую коэффициентом асимметрии 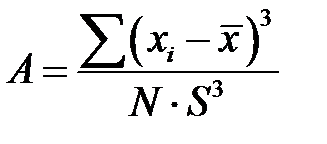
вычисления. В основу коэффициента асимметрии положено среднеквадратичное отклонение, которое даёт возможность более полно учесть крайние значения вариант. При наличии асимметрии одна сторона кривой дает большее кубическое отклонение, чем другая, и так как знак при кубическом отклонении сохраняется, то разница между суммами кубических отклонений показывает положительную либо отрицательную асимметрии.
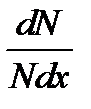
|
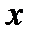
|
| a |
| б |
| в |
| Рис.2-1.4. Распределения с разными показателями эксцесса |
Показатель эксцесса выражается следующей формулой:
 .
.
Если Е > 1 , то эксцесс положительный и вершина кривой будет выше нормальной, и наоборот, если Е < 1 , то эксцесс отрицательный, вершина кривой ниже нормальной (рис. 2-1.4).
Теоретическое распределение
Теоретическое распределение – это математическая модель распределения вероятности по значениям дискретной случайной величины или по интервалам непрерывной случайной величины.
Вероятность
В эмпирическом распределении относительное число попаданий в заданный интервал дается частостью 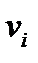 , в теоретическом распределении подобная величина называется вероятностью. Вероятность есть мера объективной возможности данного события. Вероятность связана с частостью появления переменной величины:
, в теоретическом распределении подобная величина называется вероятностью. Вероятность есть мера объективной возможности данного события. Вероятность связана с частостью появления переменной величины:
 . .
| (2-1.9) |
Вероятность выражает вполне определенную, хотя и своеобразную, связь между постоянным комплексом условий и случайным событием в поле испытаний, количественно характеризуя единство необходимого и случайного. Конкретный смысл вероятности заключается в том, что она определяет среднюю частость, с которой можно ожидать появления события в длинных сериях испытаний. Значение вероятности изменяется в пределах от нуля до единицы.
Математическое ожидание.
Среднее арифметическое, являющееся центром эмпирического распределения, переходит в математическое ожидание M ( x ) при 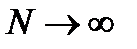 . В теоретическом распределении дискретных величин математическое ожидание
. В теоретическом распределении дискретных величин математическое ожидание
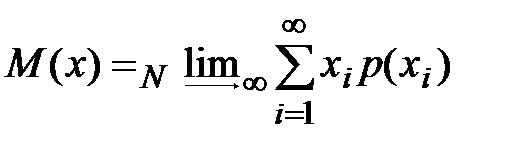 . .
| (2-1.20) |
Математическое ожидание непрерывно распределенной величины
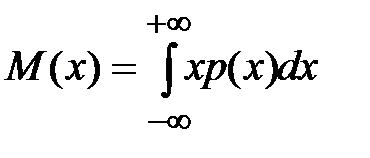 . .
| (2-1.21) |
При многократных экспериментальных определениях некоторой величины в одних и тех же условиях (при отсутствии систематических погрешностей) математическое ожидание можно рассматривать как "истинное" значение этой величины.
Дисперсия
В теоретическом распределении дисперсия 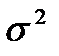 есть математическое ожидание квадрата отклонений случайной величины от её математического ожидания
есть математическое ожидание квадрата отклонений случайной величины от её математического ожидания
 . .
| (2-1.22) |
Если обозначить M(x) = a, то дисперсия распределения дискретной величины может быть записана как
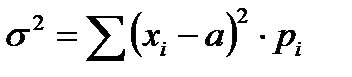 , ,
| (2-1.23) |
в случае непрерывной величины как
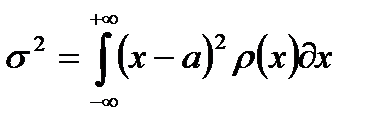 . .
| (2-1.24) |
Экспериментальная часть
Приборы и принадлежности
1. Пересчетный прибор ПС-02-08 (или ПП-16).
2. Секундомер.
Порядок выполнения работы
1. Ознакомиться с инструкцией работы пересчетного прибора.
2. Получить статистическую совокупность вариант частоты электрических сигналов за время 10 секунд. Объем совокупности N = 100.
3. Провести обсчет полученных результатов с помощью программы Excel. Для этого занести в Excel данные и построить таблицу 2-2.1. Провести группировку полученной статистической совокупности от меньшего к большему, найти 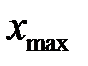 и
и 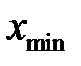 , Dx определить, выбрать число интервалов К, найти ширину интервала D h, определить границы интервала. Определить отклонения вариант от среднего значения, квадраты этих отклонений, их кубы и четвертые степени. Рассчитать
, Dx определить, выбрать число интервалов К, найти ширину интервала D h, определить границы интервала. Определить отклонения вариант от среднего значения, квадраты этих отклонений, их кубы и четвертые степени. Рассчитать 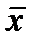 - среднее по всем значениям, S – среднее квадратичное, доверительный интервал
- среднее по всем значениям, S – среднее квадратичное, доверительный интервал 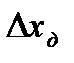 (используя коэффициенты Стьюдента
(используя коэффициенты Стьюдента 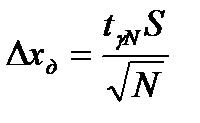 , где g - доверительная вероятность равная 0,95), асимметрию и эксцесс. Сделать вывод о принадлежности экспериментального распределения к нормальному.
, где g - доверительная вероятность равная 0,95), асимметрию и эксцесс. Сделать вывод о принадлежности экспериментального распределения к нормальному.
Таблица 2-2.1
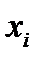
| 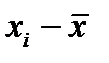
| 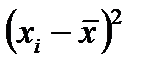
| 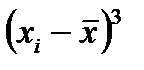
| 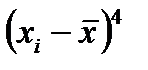
|
| x1 | ||||
| … | ||||
| xn | ||||
| S (по все столбцам) | ||||
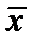
| 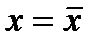 ± ± 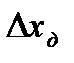
| S | A | E |
3. Рассчитать частоту n и частость n выпадения вариант. Результаты вычислений занести в таблицу 2-2.2. Построить гистограмму и полигон экспериментального распределения на миллиметровке.
Таблица 2-2.2
| № | хсреднее по интервалу | ni/N |
| 1 | ||
| … | ||
| K |
4. Графически сравнить экспериментальное распределение с распределением Гаусса при экспериментально полученных значениях 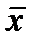 и S.
и S.
Для этого определить значение плотности вероятности экспериментального распределения предполагая, что оно подчиняется закону Гаусса и f(x) определится по формуле
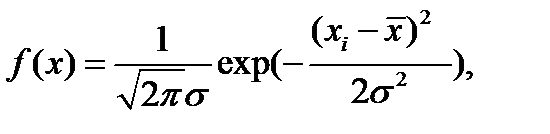 (2-1.30)
(2-1.30)
где xi – среднее по интервалу, 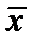 – среднее по всем значениям, для ограниченного числа измерений N. В вычислениях следует s принять равной средне квадратичному отклонению выборки измерений S. Построить таблицу 2-2.3, где D h - ширина интервала.
– среднее по всем значениям, для ограниченного числа измерений N. В вычислениях следует s принять равной средне квадратичному отклонению выборки измерений S. Построить таблицу 2-2.3, где D h - ширина интервала.
Таблица 2-2.3
| № | хсреднее по интервалу | ni/N | f(x) D h |
| 1 | |||
| 2 | |||
| … | |||
| K |
5. Построить график совместимости ni (полигон) и график f(x)Dh. Используя формулу (2-1.29) для c2 – критерия, определить его значение и сопоставить с критическим, установить принадлежность экспериментального распределения нормальному.
Контрольные вопросы
1. Что такое случайное событие, случайная величина, дискретная случайная величина, непрерывная случайная величина?
2. Что такое варианта, статистическая совокупность, частота, частость, закон распределения?
3. Что такое гистограмма, полигон? Какими свойствами они обладают?
4. Назовите основные параметры экспериментального распределения.
5. Что такое теоретическое распределение, каковы его параметры?
6. Каков смысл дифференциальной и интегральной функций нормального распределения? Как они выражаются на графике дифференциальной функции?
7. Какова связь между параметрами генеральной и выборочной совокупности?
8. Каков смысл параметрических критериев?
9. В чем заключается смысл c -критерия?
Список литературы
1. Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. М. : Наука, 1970.
2. Гмурман В.Е. Теория вероятностей и математическая статистика : учеб. пособие для вузов. М. : Высш.шк., 2004. 479с.
3. Гусак А.А. Высшая математика т.2 : учебник для студентов вузов. Мн. : ТетраСистем, 2001. 448с.
4. Физический практикум / Под ред. В.И. Ивероновой. М. : Гос. изд-во физико-математической литературы, 1962. 956с.
Лабораторная работа 2-2
Молекулярное строение жидкостей и методы определения коэффициента поверхностного натяжения
Цель работы: познакомиться с молекулярно-кинетической теорией газов и жидкостей и изучить капиллярный эффект и явление поверхностного натяжения.
Задача работы: определить коэффициент поверхностного натяжения исследуемой жидкости несколькими методами.
Теоретическая часть
Структура жидкостей
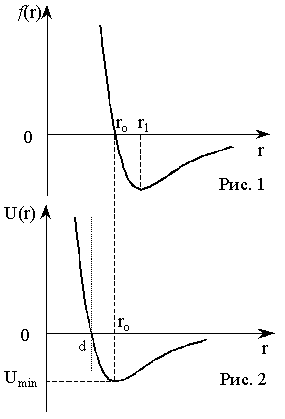
| Рис. 2-2.1. Сила межатомного вз аимодействия |
| Рис. 2-2.2. Потенциальная энергия межатомного взаимодействия |

| Рис. 2-2.1. Сила межатомного взаимодействия |
| Рис. 2-2.2. Потенциальная энергия межатомного взаимодействия |
Поверхностное натяжение
| Рис. 3 |
| Рис. 2-2.3. Силы на границе жидкость - пар |
Поверхность жидкости, соприкасающейся с другой средой (стенки сосуда, ее собственный пар, твердое тело), находится в особых условиях по сравнению с остальной массой жидкости. Возникают эти особые условия потому, что молекулы пограничного слоя жидкости, в отличие от молекул в ее глубине, окружены молекулами той же жидкости не со всех сторон.
Часть “соседей” поверхностных молекул – это частицы второй среды, с которой жидкость граничит. Эта среда может отличаться от жидкости как природой, так и плотностью частиц.
В случае, если жидкость граничит со своим собственным паром (насыщенным), т. е. в случае, когда мы имеем дело с одним веществом, сила, направлена внутрь жидкости (рис. 2-2.3). Это объясняется тем, что плотность молекул в жидкости много больше, чем в насыщенном паре над жидкостью (вдали от критической температуры), и поэтому сила притяжения, испытываемая молекулой поверхностного слоя со стороны молекул жидкости, больше, чем со стороны молекул пара.
Отсюда следует, что при увеличении поверхности жидкости некоторое число молекул из объема жидкости должно быть поднято в поверхностный слой. Для этого необходимо произвести внешнюю работу. Если при постоянной температуре обратимым путем изменить поверхность жидкости на бесконечно малую величину dS, то необходимая для этого работа
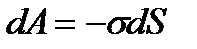 . (2-2.2)
. (2-2.2)
Знак минус указывает на то, что увеличение поверхности (dS > 0) сопровождается отрицательной (затраченной) работой.
Коэффициент 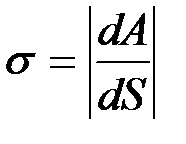 является основной величиной, характеризующей свойства поверхности жидкости, и называется коэффициентом поверхностного натяжения. Следовательно, коэффициент поверхностного натяжения измеряется работой, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.
является основной величиной, характеризующей свойства поверхности жидкости, и называется коэффициентом поверхностного натяжения. Следовательно, коэффициент поверхностного натяжения измеряется работой, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.
С другой стороны, из термодинамики известно, что при изотермических процессах роль потенциальной энергии играет свободная энергия, для которой справедливо соотношение dF = -dA, где dA – работа, связанная с возникновением свободной энергии dF (свободной энергией системы называется та ее часть, которая может быть превращена в работу). В результате однородности поверхности очевидно, что свободная энергия пропорциональна площади поверхности.
На основании сказанного выше с учетом (2-2.2) можно написать:
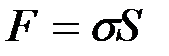 , (2-2.3)
, (2-2.3)
т. е. коэффициент поверхностного натяжения жидкости можно определить как свободную энергию жидкости, приходящуюся на единицу ее поверхности. В системе СИ s имеет размерность Дж/м2 или Н/м. Поверхностное натяжение зависит от свойств жидкости и изменяется в широких пределах. Например, при 200С для воды s = 0,073 Н/м, для ртути s = 0,465 Н/м.
Капиллярные явления
| h |
| стекло |
| R=r |
| h |
| вода |
| ртуть |
| Рис. 2-2.6. Жидкости в капиллярах |
Рассмотрим поверхность жидкости, опирающуюся на некоторый плоский контур. Если поверхность жидкости не плоская, то стремление ее к сокращению под действием сил поверхностного натяжения приведет к возникновению давления, дополнительно к тому, которое испытывает жидкость с плоской поверхностью. В случае выпуклой поверхности это
| Р0 |
| Р0+DР |
| Р0-DР |
| Рис. 2-2.7. Силы поверхностного натяжения |
Величина добавочного давления над произвольной поверхностью вычисляется по формуле Лапласа:
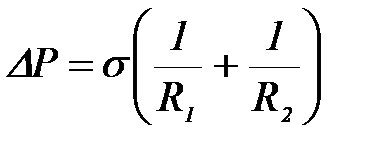 . (2-2.6)
. (2-2.6)
Здесь R1 и R2 – радиусы кривизны поверхностного слоя, величина 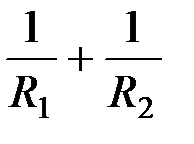 называется средней кривизной произвольной поверхности в данной точке. Если поверхность сферическая, то R1 = R2 и
называется средней кривизной произвольной поверхности в данной точке. Если поверхность сферическая, то R1 = R2 и
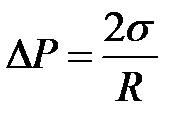 , (2-2.7)
, (2-2.7)
где R – радиус сферы. Добавочное давление D Р (иногда его называют лапласовым давлением) обусловливает изменение уровня жидкости в капиллярных трубках. Поэтому его еще называют капиллярным давлением.
Если жидкость полностью смачивает стенки капилляра, то поверхность ее имеет вогнутую форму ( D Р < 0), если полностью не смачивает – выпуклую ( D P > 0). Поэтому в случае смачивания капилляра уровень жидкости в нем будет выше, чем с сосуде при не смачивании (рис. 2-2.6). Жидкость поднимается или опускается в капилляре до тех пор, пока добавочное давление D Р не сравняется с гидростатическим давлением поднявшегося или опустившегося столба жидкости. Если считать, что жидкость полностью смачивает поверхность капилляра, то радиус кривизны мениска R совпадает с внутренним радиусом трубки r. По равенству лапласова и гидростатического давления можно записать:
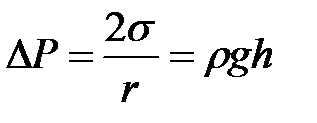 , (2-2.8)
, (2-2.8)
где r – плотность жидкости, h – высота ее поднятия, g – ускорение силы тяжести.
Из равенства (2-2.8) можно определить коэффициент поверхностного натяжения:
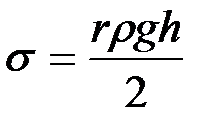 . (2-2.9)
. (2-2.9)
Формула (9) используется в качестве рабочей при определении коэффициента поверхностного натяжения капиллярным методом.
Экспериментальная часть
Приборы и принадлежности
Бюретка с краном на штативе, химический стаканчик, исследуемая жидкость и вода.
Вывод рабочей формулы
Возьмем две жидкости, заключенные в один и тот же объем. Массы этих жидкостей можно представить в виде:
 ,
,
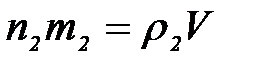 ,
,
где m1, m2 – масса одной капли соответствующих жидкостей; n1, n2 – количество их капель; ρ1, ρ2 – плотности этих жидкостей, V – объем, занимаемый каждой из этих жидкостей.
В момент отрыва капли жидкости имеем (для n капель):

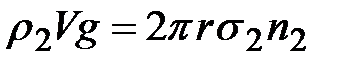 .
.
После преобразования приходим к выражению, представляющему рабочую формулу метода и выражающему величину поверхностного натяжения исследуемой жидкости через аналогичную характеристику вспомогательной жидкости (в данном случае – воды):
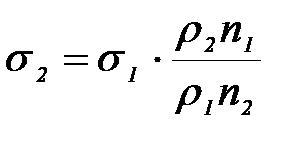 . (2-2.10)
. (2-2.10)
Порядок выполнения работы
1. Промыь бюретку и наполнить ее через воронку водой (объем 20-25мл).
2. Добиться с помощью крана равномерного падания капель.
3. Подставляя мерный стаканчик (химический стакан с делениями), посчитать количество капель n1 воды, соответственно заданному объему.
4. Налить в бюретку исследуемую жидкость (объем 20-25мл), предварительно промыв ею бюретку, и определяют количество капель n2 этой жидкости в том же объеме.
5. Взяв из таблицы значения , 2, s1 при данной температуре, по формуле (10) найти s 2.
6. Результаты измерений и вычислений занести в табл. 2-3.1.
Таблица 2-2.1
| № | s1, Н/м | r1, кг/м3 | r2, кг/м3 | Т, К | n1 | n2 | s2, Н/м |
| 1 | |||||||
| 2 | |||||||
| 3 |
Задача 2. Определение коэффициента поверхностного натяжения методом компенсации разности давлений поверхностного слоя жидкости (метод Штейна)
Приборы и принадлежности
Установка, набор исследуемых жидкостей, груша, капилляр.
Описание установки
Установка состоит из капилляра А, широкой трубки Д и водяного манометра С, сообщающихся посредством трубки В. Широкую трубку Д опускают в стакан с водой, помещенный на столике, который можно закрепить винтом Е в любом положении. Опуская и поднимая столик, можно изменить давление в рассматриваемой системе.
Вывод рабочей формулы
Как мы уже установили выше, если капилляр опустить в сосуд с исследуемой жидкостью, то в случае смачивания стенок капилляра этой жидкостью, последняя поднимется на некоторую высоту (dР < 0). Если теперь увеличить внешнее давление над поверхностью жидкости в капилляре, скомпенсировав тем самым Лапласово давление dР, то уровень жидкости в капилляре опустится до уровня жидкости в сосуде и сравняется с ним.
Если внешнее давление при этом увеличилось на Р, то согласно (8)
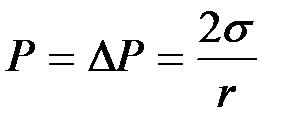 , (2-2.11)
, (2-2.11)
где r – радиус капилляра.
С другой стороны, избыток давления Р в системе можно выразить так:
 , (2-2.12)
, (2-2.12)
где h – разность уровней воды в манометре, r - плотность жидкости, налитой в манометр. Выражая из (2-2.11) и (2-2.12) s , получим
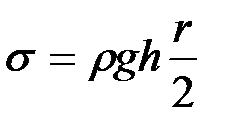 . (2-2.13)
. (2-2.13)
Порядок выполнения работы
1.
| С |
| Д |
| Е |
| В |
| А |
| Рис. 2-2.8. Схема опыта |
2. Медленно поднимают столик Е и доводят уровень жидкости в капилляре до ее уровня в стаканчике (рис. 2-2.8). Закрепляют столик и определяют разность уровней манометра (h). Опыт проделывают несколько раз, перемещая столик и заново отсчитывая разность уровней h.
Примечание. Ввиду большой зависимости коэффициента поверхностного натяжения от температуры, необходимо указать температуру, при которой производились наблюдения.
3. Результаты измерений и вычислений заносят в табл. 2-3.2.
Таблица 2-2.2
| Номер опыта | Т, К | h, м | r, м | s, Н/м | 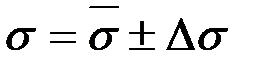 , Н/м , Н/м
|
| 1 |
| ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 |
Проводят статистическую обработку результатов по методу Стьюдента при a = 0.95 (доверительная вероятность).
Приборы и принадлежности
Аналитические весы, набор жидкостей, разновес, стеклянная кювета, металлическое кольцо.
Порядок выполнения работы
1. Измеряют штангенциркулем внешний диаметр кольца d2 и определяют толщину стенок кольца h.
2. Подвешивают кольцо на левое коромысло весов и уравновешивают их с помощью разновеса.
3. Подводят под кольцо кюветку с исследуемой жидкостью так, чтобы оно только коснулось поверхности жидкости.
4. Осторожно нагружают правую чашку весов разновесами до тех пор, пока кольцо не оторвется от поверхности жидкости. Вес разновесок равен при этом силе поверхностного натяжения f.
Внимание! Рекомендуется класть разновесы на предварительно арретированные весы.
Опыт повторяют 3 – 5 раз.
5. По формуле (2-2.14) определяют коэффициент поверхностного натяжения жидкости s.
6. Результаты измерений и вычислений заносят в таблицу 2-3.3
Таблица2-3. 3
| № опыта | d2, м | h, м | f, Н | s, Н/м | D s, Н/м | 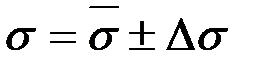 , Н/м , Н/м
|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 |
Проводят статистическую обработку результатов по методу Стьюдента при a = 0,95.
Приборы и принадлежности
Бюретка с краном на штативе, химический стакан, исследуемые жидкости, аналитические весы, отчетный микроскоп.
Порядок выполнения работы
1. Наполнить бюретку исследуемой жидкостью (объем 20 - 25мл) и с помощью крана добиваются равномерного падения капель в стакан.
2. Установить отсчетный микроскоп на уровне шейки капли, добиваются четкого ее изображения. Измеряют 10 раз диаметр шейки в момент отрыва. Цена деления микроскопа равна 0,02 мм/дел.
3. Взвешивают на аналитических весах пустой химический стаканчик. Не меняя скорости падения капель, наполняют его 100 каплями жидкости и вновь взвешивают. Если масса пустого стаканчика равна m1, а с жидкостью m2, тогда масса одной капли будет  . Опыт по определению m1 и m2 проводят несколько раз.
. Опыт по определению m1 и m2 проводят несколько раз.
4. Подставляя полученные значения m и r в формулу метода (2-2.15), определяют значение s для воды и спирта.
5. Результаты измерений и вычислений заносят в табл. 2-2.4 4.Проводят статистическую обработку результатов по методу Стьюдента для a=0,95.
6. Окончательный результат представляют в виде: 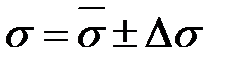 .
.
Таблица2-2. 4.
| № | Жидкость | r, м | m1, кг | m2, кг | m, кг | s, Н/м |
| 1 | Вода | |||||
| 2 | ||||||
| 3 | ||||||
| 1 | Спирт | |||||
| 2 | ||||||
| 3 |
Контрольные вопросы и задания
1. Начертите кривые взаимодействий f(r) и U(r) и объясните ход этих зависимостей.
2. Запишите формулу для потенциала Леннарда – Джонса и объясните ее содержание.
3. При каком соотношении кинетической и потенциальной энергий состояние системы является газом?
4. Объясните механизм возникновения сил поверхностного натяжения.
5. Почему при отсутствии внешних сил капля жидкости принимает форму шара?
6. Дайте определение коэффициента поверхностного натяжения жидкости и запишите формулу для s.
7. Запишите формулу Лапласа и объясните причину поднятия (опускания) жидкости в капилляре.
8. При каких условиях отрывается капля жидкости, вытекающей из трубки?
9. Получите формулу для определения s методом сравнения.
10. Объясните принцип действия экспериментальной установки Штейна для определения s. Каково назначение широкого сосуда Д?
11. Запишите условие отрыва кольца от поверхности жидкости.
12. Приведите примеры проявления сил поверхностного натяжения в природе.
Список литературы
1. Матвеев А. Н. Молекулярная физика. М., 1983.
2. Кикоин А. К., Кикоин И. К. Молекулярная физика. М., 1976.
3. Ширяева С.О., Григорьев О.А. О влиянии эффекта релаксации поверхностного натяжения на спектр движений жидкости с заряженной свободной поверхностью // ЖТФ, 2000, Т.70, Вып.6.
4. Лапшин В.Б., Сидоренко А.В. Взаимодействие гравитационно-капиллярных структур в поверхностном слое океана. «Исследовано в России» // Электронный многопредметный научный журнал, МФТИ, 1998, С. 1561-1570.
5. http://zhurnal.ape.relarn.ru/articles/2001/135.pdf
Лабораторная работа 2-3
Теоретическая часть
В молекулярной физике мы часто имеем дело с такими физическими явлениями, как диффузия, теплопроводность, внутреннее трение. Теория этих явлений основана на понятиях средней длины свободного пробега и эффективного диаметра молекул газа. Рассмотрим эти понятия.
| Рис. 2-3.1. Траектория молекулы |
Выясним теперь, почему так происходит на примере идеального газа. Если бы частицы газа представляли материальные точки, они никогда бы не сталкивались друг с другом. Поэтому при рассмотрении столкновений молекул в газе их представляют в виде твердых шаров некоторого радиуса r. Столкновения между молекулами происходят всякий раз, когда центры двух молекул окажутся на расстоянии не больше, чем 2r друг от друга. На рис. 2-3.2 как раз изображен цилиндр радиусом 2r . Штриховая прямая представляет собой путь, по которому следовала бы одна из молекул, если бы она не испытывала столкновений. Столкновение произойдет, если центр другой молекулы окажется внутри этого цилиндра. Безусловно, как только произойдет столкновение, направление движения частицы изменится и вмести с ним изменится наш воображаемый цилиндр, но для упрощения вычислений мы не будем менять вид цилиндра. Предположим, что данная молекула – одна из многих, движущихся в газе со скоростью 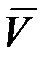 .
.
| V |
| 2r |
| r |
| V D t |
| Рис. 2-3.2. Столкновения частиц |
Представим себе на мгновение, что другие молекулы не движутся и, что концентрация молекул равна n . Тогда число молекул, центры которых лежат внутри цилиндра, определится как концентрация n , умноженная на объем этого цилиндра. Это число будет равно также и числу произошедших столкновений, обозначим его z. За промежуток времени 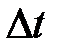 молекула пройдет расстояние
молекула пройдет расстояние 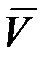
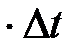 , в этом случае объем цилиндра равен π (2r)2
, в этом случае объем цилиндра равен π (2r)2 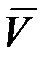
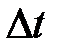 (рис. 2-3.2). Таким образом, число столкновений z за время
(рис. 2-3.2). Таким образом, число столкновений z за время 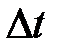 равно n π (2r)2
равно n π (2r)2 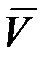
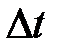 . Мы определили среднюю длину свободного пробега l как среднее расстояние между столкновениями; это расстояние равно расстоянию, пройденному за время
. Мы определили среднюю длину свободного пробега l как среднее расстояние между столкновениями; это расстояние равно расстоянию, пройденному за время 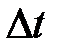 , деленному на число столкновений, произошедших за время
, деленному на число столкновений, произошедших за время 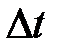 :
:
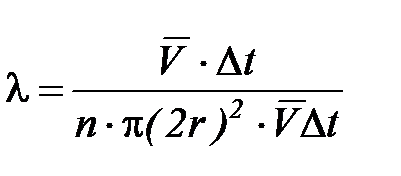 . (2-3.1)
. (2-3.1)
Однако выражение (2-3.1) является не совсем точным, поскольку мы предположили, что остальные молекулы неподвижны. В действительности они движутся, и число столкновений за время 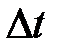 должно зависеть от относительной скорости сталкивающихся молекул, а не от
должно зависеть от относительной скорости сталкивающихся молекул, а не от 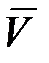 . Следовательно, число столкновений в секунду равно n π (2r)2
. Следовательно, число столкновений в секунду равно n π (2r)2 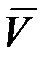 отн
отн 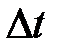 , где
, где 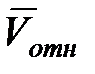 – средняя относительная скорость сталкивающихся молекул. Максвелл, используя функцию распределения молекул по скоростям, показал, что
– средняя относительная скорость сталкивающихся молекул. Максвелл, используя функцию распределения молекул по скоростям, показал, что
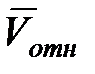 .=
.= 
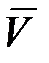 [1] *.
[1] *.
Следовательно, средняя длина свободного пробега в уравнении (1) принимает вид
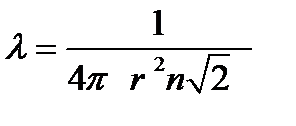 . (2-3.2)
. (2-3.2)
Как видно из последнего выражения, средняя длина свободного пробега зависит от концентрации молекул газа. Если воспользоваться основным уравнением молекулярно кинетической теории идеального газа и записать n = P / kT , то из выражения
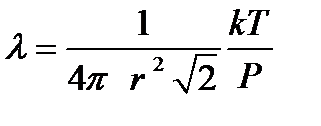 . .
| (2-3.3) |
| d |
| Рис. 2-3.3. Эффективный диаметр молекулы |
Выше мы отмечали, что молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 2-3.3.).
Величина σ = π d 2 также является важной характеристикой при изучении кинематического движения частиц и называется эффективным сечением молекулы. Тогда выражение (2-3.3) может быть представлено в форме 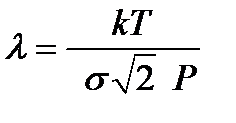 . Откуда
. Откуда
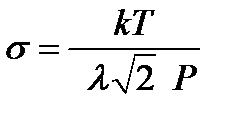 . (2-3.4)
. (2-3.4)
При нормальных условиях n ~1025 средняя длина свободного пробега молекул воздуха равна 10 –6м, в то время как диаметр молекул N2 и O2 имеет порядок приблизительно 10-10 м. Рассматриваются только парные столкновения. Случаи, когда в реальных газах сближаются и начинают взаимодействовать три молекулы и больше, маловероятны и по этой причине не принимаются во внимание. Хотя эффективное сечение σ представлено здесь в геометрическом смысле, оно несколько уменьшается с повышением температуры. Объяснение этому было дано Сезерлендом [2]: σ= σ0(1+С/T), где С – постоянная, называемая постоянной Сезерленда, имеет размерность температуры. Он использовал модель твердых шаров, но учел силы притяжения, с которыми молекулы действуют друг на друга в промежутках между столкновениями. С ростом температуры молекула несколько меньше времени находится в поле влияния другой молекулы и пролетает мимо нее без «захвата», что и приводит к увеличению длины свободного пробега молекул. Поэтому эффективное сечение у одних и тех же частиц для различных процессов может быть различным.
| P1 |
| P2 |
| X |
| Рис. 2-3.4. Механизм возникновения вязкости |
Одним из способов определения длины свободного пробега и эффективного диаметра молекул газа является определение этих характеристик с использованием явления внутреннего трения. Представим себе, что газ протекает по трубе цилиндрического сечения. Скорости отдельных слоев в потоке различны: с наибольшей скоростью движется слой газа в средней части капилляра, а по мере приближения к стенкам скорость убывает, у самой стенки имеется слой газа с нулевой скоростью, так как молекулы газа абсорбируются поверхностью (прилипают к ней) (рис. 2-3.4).Таким образом, поперек направления движения наблюдается градиент скорости движущихся слоев газа. Для поддержания движения газа по трубе необходимо создать разность давлений на ее концах. Однако в результате теплового движения молекулы, перемещаясь из более быстрого слоя в более медленный и обратно, переносят при этом импульс и при столкновениях друг с другом обмениваются импульсами. В результате скорость направленного движения быстро движущегося слоя уменьшается, а медленно движущегося слоя – увеличивается. На границе раздела слоев возникают силы внутреннего трения. Необходимо помнить, что силы вязкости являются тангенциальными силами, т.е. направлены вдоль поверхности соприкасающихся слоев.
Тогда поток импульса через единицу площади DS границы раздела двух слоев газа определяется величиной градиента скорости 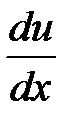
| K |
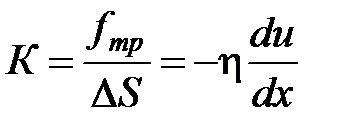 , где h – коэффициент внутреннего трения или динамической вязкости. Знак «минус» означает, что поток импульса и вектор градиента скорости направлены в противоположные стороны.
, где h – коэффициент внутреннего трения или динамической вязкости. Знак «минус» означает, что поток импульса и вектор градиента скорости направлены в противоположные стороны.
Величина η определяется соотношением
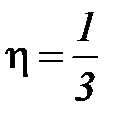 λ λ 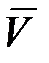 ρ, ρ,
| (2-3.5) |
где ρ -плотность газа, λ -средняя длина свободного пробега молекул, 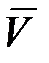 - средняя скорость молекул.
- средняя скорость молекул.
Коэффициент внутреннего трения η, как показывает молекулярно-кинетическая теория, в широких пределах от давления не зависит, так как плотность газа пропорциональна давлению, а длина свободного пробега обратно пропорциональна ему. Единицей динамической вязкости в СИ является Па с (Пуаз), т.е. это вязкость такого газа, у которого при площади соприкосновения слоев 1 м2 при градиенте скорости 1 м/с возникает сила внутреннего трения, равная 1 Н (1Пз = 0,1 Н с/м2).
При увеличении скорости или поперечных размеров потока характер течения существенным образом изменяется – возникает энергичное перемешивание жидкости. Такое течение называется турбулентным. Ламинарным или турбулентным является движение жидкости или газа в зависимости от того, насколько значительную роль играют силы трения. Английский ученый Рейнольдс установил критерий (число Рейнольдса Rе), по которому ламинарное течение переходит в турбулентное. Число Rе характеризует относительную роль сил вязкости, т.к. оно характеризует отношение кинетической энергии движения элемента жидкости к потере ее, обусловленной работой сил вязкости. Таким образом, число Рейнольдса определяет относительную роль инерции и вязкости жидкости при течении. Чем меньше число Рейнольдса, тем большую роль играют силы вязкости в движении жидкости или газа. При значениях числа Rе<1000 – течение, как правило, носит ламинарный характер. При бόльших значениях числа Рейнольдса течение приобретает турбулентный характер, заметим, что турбулентность в гладких трубах наступает при значении Reкр~1160.
Итак, в данной задаче требуется определить газокинетические характеристики молекул воздуха: длину свободного пробега и эффективный диаметр по коэффициенту внутреннего трения в газах. При ламинарном течении газа по капилляру, т.е. течении, при котором различные слои газа текут хотя и с разными скоростями, но параллельно друг другу, справедлива формула Пуазейля . Объем газа, протекающего при стационарном течении через капилляр за время t:

| (2-3.6) |
где r - радиус капилляра, 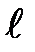 - его длина, D P - разность давлений на концах капилляра. Откуда следует выражение для коэффициента вязкости:
- его длина, D P - разность давлений на концах капилляра. Откуда следует выражение для коэффициента вязкости:
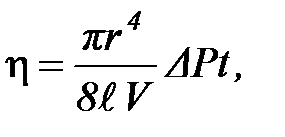
| (2-3.7) |
Исходя из выражения (5), можно определить среднее значение длины свободного пробега, т.е.
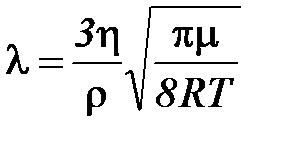 и и 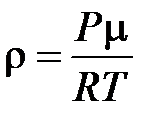 , ,
| (2-3.8) |
где Р - давление воздуха в помещении, определяемое по барометру, Т -температура воздуха в градусах Кельвина.
Из выражения (4) можно найти эффективное сечение, а затем и эффективный диаметр молекул воздуха.
Экспериментальная часть
Порядок выполнения работы
1. Подставив измерительный стакан 3 (рис. 2-3.5), открыть кран 4 и дождаться, когда установится стационарный процесс (вода начнет вытекать каплями). В этот момент оценить разность уровней давлений в коленах манометра D Р.
2. Подставить другой пустой мерный стаканчик под кран (масса которого предварительно определена) засечь время t , за которое объем жидкости составит примерно 20 см3. Для точного определения объема жидкость рекомендуется взвесить. Температуру воздуха, атмосферное давление, плотность воды и воздуха при условиях эксперимента внести в табл.2-3.1.
Параметры установки и условия проведения опыта Таблица 2-3.1
| r, мм | 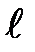 ,мм ,мм
| T,К | P,кг/м3 | r, кг/м3 (вода) | r, кг/м3 (воздух) |
3. Рассчитать значения h, l, s по формулам (2-3.7, 2-3.8, 2-3.4). Опыт повторить три раза. Вычислить погрешности измерений при доверительной вероятности a= 0.95.
4. Вычислить скорость Ucp. скорость потока (среднюю по сечению капилляра): Ucp=(V/t)pr2 , где r - радиус капилляра, V - объем воздуха, прошедшего через капилляр, равный объему воды, вытекшей за время t.
5. Рассчитать число Рейнольдса по формуле: Rе=rUсрr/h, где r - плотность воздуха в условиях опыта. Убедиться, что эксперимент проходил при ламинарном течении.
6. Записать окончательные результаты измеряемых величин η, λ, s. Оценить величины погрешностей измерения при a = 0.95.
Экспериментальные результаты Таблица 2
| № | Dh, мм | V,мл | DP, Па | t,с | Uср., мл/с | h, Па с | l,м | s,м2 |
Контрольные вопросы и задания
1. Дайте определение понятия «средняя длина свободного пробега» молекул. Получите математическое выражение длины свободного пробега молекул газа. Как зависит эта величина от давления и температуры газа?
2. Что понимается под эффективным сечением молекул газа. Зависит ли эта величина от температуры газа?
3. Чему равна средняя относительная скорость молекул газа? Дайте математический вывод этого соотношения.
4. В чем суть явления внутреннего трения в газах. Запишите закон Ньютона.
5. Как определяется величина коэффициента вязкости, в каких единицах он измеряется?
6. Запишите формулу Пуазейля и поясните ее смысл.
7. Что характеризует число Рейнольдса?
8. В чем суть экспериментального метода определения средней длины свободного пробега молекул газа?
9. Объясните условие отрыва капель от крана. Какую роль при этом играет уровень воды в сосуде?
Список литературы
1. Матвеев А.Н. Молекулярная физика. М.: Высшая школа,1987.
2. Сивухин Д.В. Общий курс физики. М.: Наука, 1990. Т. 2,
3. Хайкин Э.С. Физические основы механики. М.: Наука, 1971.
4. Основы физики. Курс общей физики. Квантовая и статистическая физика / Под. ред. Ю.М. Ципенюка. М.: Физ.-мат. лит., 2001. Т.2.
Лабораторная работа 2-4
Теоретическая часть
Для наиболее общей характеристики свойств тел пользуются понятием агрегатных состояний – газообразного, жидкого и твердого.
Благодаря большой разреженности вещества в газообразном состоянии его молекулы находятся сравнительно далеко друг от друга: на расстояниях, больших по сравнению с их собственными размерами. В газах молекулы не связаны между собой стационарными, устойчивыми связями. Молекулы постоянно изменяют относительные взаимные положения. Поэтому взаимодействие между молекулами газа играет второстепенную роль; большую часть времени молекулы движутся как свободные, лишь сравнительно редко испытывая столкновения друг с другом.
В жидкостях же молекулы сближены на расстояния, сравнимые с их собственными размерами, они плотно заполняют занимаемое жидкостью пространство и сравнительно медленно меняют взаимное положение. В течение сравнительно продолжительных промежутков времени группы молекул могут образовывать агрегаты молекул. Эти агрегаты молекул по своим свойствам напоминают твердое тело, т.е. молекулы жидкостей находятся в сильном постоянном взаимодействии.
В обычных условиях жидкости и газы настолько отличаются друг от друга по своей плотности, что различить их не представляет никакой трудности. Тем не менее, различие между этими двумя состояниями вещества в действительности не принципиальное, а лишь количественное – в количественной величине плотности и связанной с этим разнице в интенсивности взаимодействия молекул. Отсутствие принципиального отличия между ними в особенности ясно проявляется в том, что переход между состояниями, которые мы называем жидким и газообразным, может быть произведен вполне непрерывным образом, так что мы ни в какой момент не смогли бы указать, где кончилось одно состояние и началось другое.
Количественный характер имеет также и различие между жидкостями и так называемыми аморфными (не кристаллическими) твердыми телами; к последним относятся стекло, различные смолы (например, канифоль) и т.п., и здесь отсутствие принципиальной разницы ясно проявляется в возможности непрерывного перехода из одного состояния в другое. В этом случае такой переход осуществляется путем простого нагревания. Так, твердое стекло при нагревании постепенно размягчается, становясь в конце концов вполне жидким; этот процесс совершенно непрерывен, и в нем не существует никакого определенного «момента перехода». По своей плотности аморфное тело отличается от получающейся из него жидкости лишь незначительно. Основным количественным различием между ними является разница по величине их вязкости, т. е. в их «текучести».
Общим свойством газов, жидкостей и аморфных твердых тел является беспорядочность распределения молекул в них. Эта беспорядочность обусловливает собой изотропию этих тел – одинаковость этих свойств по всем направлениям. Свойство изотропии принципиально отличает эти тела от анизотропных кристаллических твердых тел, в которых атомы расположены строго упорядоченным образом.
Таким образом, из трех обычных состояний вещества (твердое, жидкое, газообразное) жидкости по своей структуре и межмолекулярным силам имеют как свойства газа, так и свойства твердых тел. Они занимают промежуточное положение.
В жидкостях, как и в газах, наблюдаются явления диффузии, теплопроводности и вязкости. Однако механизм этих процессов в жидкостях иной, чем в газах. Явления переноса в газах определяются длиной свободного пробега молекул. Поэтому выражения для всех коэффициентов переноса содержат в качестве множителя длину свободного пробега молекул. В жидкостях, как и в очень плотных газах, понятие длины свободного пробега теряет смысл, так как среднее расстояние между молекулами сравнимо с размерами самих молекул. Молекулы жидкости могут лишь совершать малые колебания в пределах, ограниченных молекулярными расстояниями. Однако время от времени колеблющаяся молекула может получить от соседних молекул избыточную энергию, достаточную для того, чтобы совершить скачок на некоторое расстояние. Такие колебания, сменяющиеся скачками, представляют тепловое движение молекул жидкости. Ежесекундно молекула жидкости успевает переменить место около 108 раз, совершив между двумя последовательными переходами 103¸105 колебаний.
Рассматривая протекающие в газах процессы, мы использовали понятие идеального газа. Идеальная жидкость, т.е. жидкость без трения, является абстракцией. Всем реальным жидкостям и газам в большей или меньшей степени присуща вязкость или внутреннее трение. Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается.
Состояние движения жидкости можно определить, указав для каждой точки пространства вектор скорости 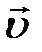 как функцию времени. Величина и направление вектора
как функцию времени. Величина и направление вектора 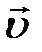 в каждой точке могут меняться со временем. Если вектор скорости в каждой точке пространства остается постоянным, то течение называется установившимся или стационарным. При стационарном течении любая частица жидкости проходит данную точку пространства с одним и тем же значением
в каждой точке могут меняться со временем. Если вектор скорости в каждой точке пространства остается постоянным, то течение называется установившимся или стационарным. При стационарном течении любая частица жидкости проходит данную точку пространства с одним и тем же значением 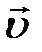 .
.
Наблюдается два вида течения жидкости (или газа). Если жидкость как бы разделена на слои, которые скользят друг относительно друга, не перемешиваясь, то течение называется ламинарным. Если в такой поток ввести подкрашенную струйку, то она сохранится, не размываясь по всей длине потока, так как в ламинарном потоке частицы жидкости не переходят из одного слоя в другой. Ламинарное течение стационарно.
При увеличении скорости потока может наблюдаться перемешивание слоев жидкости. Такое движение называется турбулентным. При турбулентном течении скорость частиц в каждом данном месте все время изменяется беспорядочным образом – течение нестационарное. Если в турбулентный поток ввести окрашенную струйку, то уже на небольшом расстоянии от места ее введения окрашенная жидкость равномерно распределится по всему сечению потока.
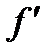
|
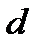
|
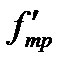
|
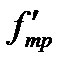
|
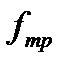
|
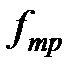
|
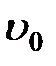
|
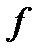
|
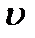
|
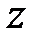
|
| Рис. 2-4.1. Градиент скорости течения жидкости |
Для выяснения закономерностей, которым подчиняются силы внутреннего трения, рассмотрим следующий опыт. Погрузим в жидкость две параллельные друг другу пластины (рис. 2-4.1). Пусть линейные размеры пластин значительно превосходят расстояние между пластинами (  ). Нижнюю пластину закрепим на месте. Верхнюю пластину приведем в движение с некоторой скоростью
). Нижнюю пластину закрепим на месте. Верхнюю пластину приведем в движение с некоторой скоростью 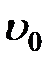 относительно нижней. Для перемещения верхней пластины с постоянной скоростью
относительно нижней. Для перемещения верхней пластины с постоянной скоростью  необходимо действовать на неё с вполне определенной, постоянной по величине силой
необходимо действовать на неё с вполне определенной, постоянной по величине силой  . Поскольку верхняя пластина движется равномерно со скоростью
. Поскольку верхняя пластина движется равномерно со скоростью  , без ускорения, действие этой силы уравновешивается равной ей по величине противоположно направленной силой, которая, очевидно, есть сила трения, действующая на пластину при её движении в жидкости. Обозначим ее
, без ускорения, действие этой силы уравновешивается равной ей по величине противоположно направленной силой, которая, очевидно, есть сила трения, действующая на пластину при её движении в жидкости. Обозначим ее 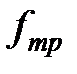 .
.
Варьируя скорость пластины 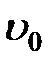 , площадь пластин
, площадь пластин 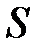 и расстояние между ними
и расстояние между ними  , можно получить, что
, можно получить, что
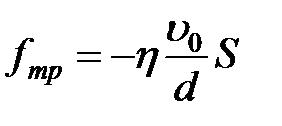 , (2-4.1)
, (2-4.1)
где  - коэффициент пропорциональности, зависящий от природы и состояния (например, температуры) жидкости и называемый коэффициентом внутреннего трения или коэффициентом вязкости, или просто вязкостью жидкости (газа).
- коэффициент пропорциональности, зависящий от природы и состояния (например, температуры) жидкости и называемый коэффициентом внутреннего трения или коэффициентом вязкости, или просто вязкостью жидкости (газа).
Нижняя пластина при движении верхней также оказывается подверженной действию силы 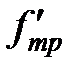 , равной по величине
, равной по величине 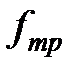 . Для того чтобы нижняя пластина оставалась неподвижной, силу
. Для того чтобы нижняя пластина оставалась неподвижной, силу 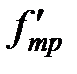 необходимо уравновесить с помощью силы
необходимо уравновесить с помощью силы 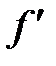 .
.
Таким образом, при движении двух погруженных в жидкость пластин друг относительно друга между ними возникает взаимодействие, характеризуемое силой (2-4.1). Воздействие пластин друг на друга осуществляется, очевидно, через жидкость, заключенную между пластинами, передаваясь от одного слоя жидкости к другому. Если в любом месте зазора провести мысленно плоскость, параллельную пластинам (см. пунктирную линию на рис. 1), то можно утверждать, что часть жидкости, лежащая над этой плоскостью, действует на часть жидкости, лежащую под плоскостью, с силой 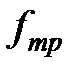 , причем величина
, причем величина 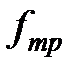 и
и 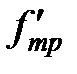 определяется формулой 2-4.1. Таким образом, формула 2-4.1 определяет не только силу трения, действующую на пластины, но и силу трения между соприкасающимися частями жидкости.
определяется формулой 2-4.1. Таким образом, формула 2-4.1 определяет не только силу трения, действующую на пластины, но и силу трения между соприкасающимися частями жидкости.
Если исследовать скорость частиц жидкости в разных слоях, то оказывается, что она изменяется в направлении 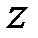 , перпендикулярном к пластинам (рис. 1), по линейному закону
, перпендикулярном к пластинам (рис. 1), по линейному закону
 . (2-4.2)
. (2-4.2)
Частицы жидкости, непосредственно соприкасающиеся с пластинами, как бы прилипают к ним и имеют такую же скорость, как и сами пластины. Согласно формуле (2-4.2),
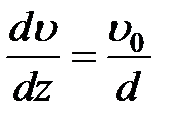 . (2-4.3)
. (2-4.3)
Используя равенство (2-4.3), формуле (2-4.1) для силы внутреннего трения можно придать вид
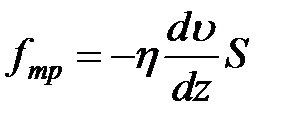 . (2-4.4)
. (2-4.4)
Величина  показывает, как быстро изменяется скорость в направлении оси
показывает, как быстро изменяется скорость в направлении оси  , и называется градиентом скорости (точнее, это – модуль градиента скорости; сам градиент – вектор).
, и называется градиентом скорости (точнее, это – модуль градиента скорости; сам градиент – вектор).
Формула (2-4.4) была нами получена для случая, когда скорость изменяется по линейному закону (в этом случае градиент скорости является постоянным). Оказывается, что эта формула остается справедливой и для любого другого закона изменения скорости при переходе от слоя к слою. В этом случае для определения силы трения между двумя граничащими друг с другом слоями нужно брать значение градиента 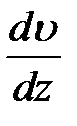 в том месте, где проходит воображаемая поверхность раздела слоев. Так, например, при движении жидкости в круглой трубе скорость равна нулю у стенок трубы, максимальна на оси трубы и, как можно показать, при не слишком больших скоростях течения изменяется вдоль любого радиуса по закону
в том месте, где проходит воображаемая поверхность раздела слоев. Так, например, при движении жидкости в круглой трубе скорость равна нулю у стенок трубы, максимальна на оси трубы и, как можно показать, при не слишком больших скоростях течения изменяется вдоль любого радиуса по закону
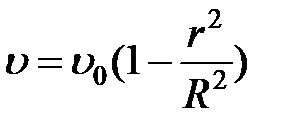 , (2-4.5)
, (2-4.5)
где 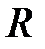 - радиус трубы,
- радиус трубы, 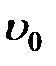 - скорость на оси трубы,
- скорость на оси трубы, 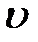 - скорость на расстоянии
- скорость на расстоянии 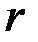 от оси трубы (рис. 2). Проведем в жидкости мысленно цилиндрическую поверхность радиуса
от оси трубы (рис. 2). Проведем в жидкости мысленно цилиндрическую поверхность радиуса  . Части жидкости, лежащие по разные стороны от этой поверхности, действуют друг на друга, с силой, величина которой в расчете на единицу поверхности равна
. Части жидкости, лежащие по разные стороны от этой поверхности, действуют друг на друга, с силой, величина которой в расчете на единицу поверхности равна
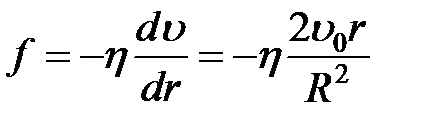 , (2-4.6)
, (2-4.6)
т.е. возрастает пропорционально расстоянию поверхности раздела от оси трубы.
Коэффициент пропорциональности  (эта) характеризует вязкость жидкости и называется коэффициентом динамической вязкости или просто вязкостью жидкости.
(эта) характеризует вязкость жидкости и называется коэффициентом динамической вязкости или просто вязкостью жидкости.
|

|
| Рис. 2-4.2. Градиент скорости течения жидкости в трубе |
Из формулы (2-4.4) следует, что
 - коэффициент динамической вязкости – будет численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся один относительно другого с градиентом скорости, равным единице.
- коэффициент динамической вязкости – будет численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся один относительно другого с градиентом скорости, равным единице.
Единицей вязкости СИ является такая вязкость, при которой градиент скорости, равный 1м/с на 1 м, приводит к возникновению силы внутреннего трения в 1н на 1м2 поверхности касания слоев. Эта единица обозначается  или Па × с. (в системе СГС коэффициент вязкости измеряется в Пуазах по имени французского ученого Пуазейля, 1Пз = 0,1 Н с/м2).
или Па × с. (в системе СГС коэффициент вязкости измеряется в Пуазах по имени французского ученого Пуазейля, 1Пз = 0,1 Н с/м2).
Динамическая вязкость жидкостей существенно зависит от температуры: с понижением температуры она увеличивается. Однако П.Л. Капицей было открыто, что жидкий гелий при температуре, близкой к абсолютному нулю (около –273 0С), переходит в особое состояние сверхтекучести, при котором вязкость резко падает и становится меньше 10-13  , т. е. практически равна нулю. Это значит, что жидкий гелий может свободно протекать через самые тонкие капилляры, щели и отверстия, непроницаемые даже для газа.
, т. е. практически равна нулю. Это значит, что жидкий гелий может свободно протекать через самые тонкие капилляры, щели и отверстия, непроницаемые даже для газа.
Динамическая вязкость обычно не очень вязких жидкостей имеет порядок 10-3  , у вязких жидкостей она возрастает в тысячи раз. Например, динамическая вязкость воды при 200С равна -1,002·10-3
, у вязких жидкостей она возрастает в тысячи раз. Например, динамическая вязкость воды при 200С равна -1,002·10-3  , бензина – 0,648·10-3
, бензина – 0,648·10-3 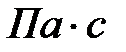 , спирта 1,2·10-3
, спирта 1,2·10-3 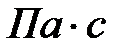 , глицерина 1480·10-3
, глицерина 1480·10-3 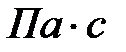 . Напомним, что вязкость газов при этой температуре и атмосферном давлении имеет порядок 10-5
. Напомним, что вязкость газов при этой температуре и атмосферном давлении имеет порядок 10-5 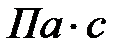 .
.
Если ввести понятие касательного напряжения ( 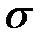 )
)

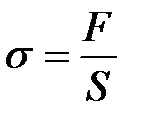 , (2-4.7)
, (2-4.7)
то выражение (2-4.4) примет вид
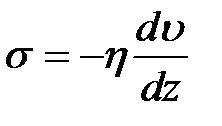 . (2-4.8)
. (2-4.8)
Преобразуем уравнение (2-4.8):
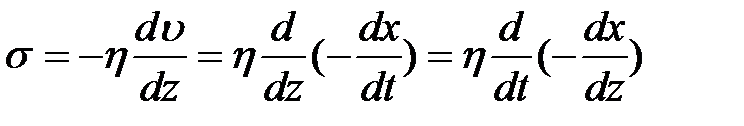 .
.
Из рис. 1 видно, что 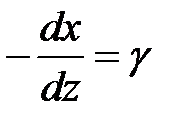 , откуда
, откуда
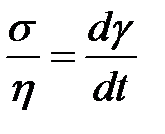 . (2-4.9)
. (2-4.9)
Таким образом, скорость сдвига пропорциональна касательному напряжению и обратно пропорциональна коэффициенту вязкости жидкости.
Для многих жидкостей коэффициент вязкости  зависит только от температуры и давления. Эти жидкости называются ньютоновскими. Уравнение (2-4.9), устанавливающее связь межу напряжением и скоростью сдвига, называется реологическим уравнением. График зависимости между скоростью сдвига и напряжением называется реологической кривой (рис.3).
зависит только от температуры и давления. Эти жидкости называются ньютоновскими. Уравнение (2-4.9), устанавливающее связь межу напряжением и скоростью сдвига, называется реологическим уравнением. График зависимости между скоростью сдвига и напряжением называется реологической кривой (рис.3).
Для ньютоновских жидкостей реологическая кривая имеет вид прямой, проходящей через начало координат. Тангенс угла наклона ее равен коэффициенту вязкости жидкости (рис. 3, кривая 1). Жидкости, для которых реологическая кривая не является прямой линией, проходящей через начало координат (рис. 3, кривые 2, 3), не являются ньютоновскими.
Вязкость ньютоновских жидкостей при постоянной температуре и давлении не остается постоянной, а зависит от скорости сдвига, от времени действия напряжения.
Кроме динамической вязкости каждая жидкость может быть охарактеризована величиной кинематической вязкости. Отношение динамической вязкости  к плотности жидкости
к плотности жидкости  называется коэффициентом кинематической вязкости
называется коэффициентом кинематической вязкости 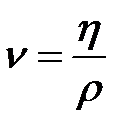 . Коэффициент кинематической вязкости измеряется в
. Коэффициент кинематической вязкости измеряется в 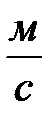 или в Стоксах – 1 Ст = 10-4 м/с.
или в Стоксах – 1 Ст = 10-4 м/с.

|
| 2 |
| 1 |
| 3 |
| arctg η |
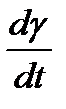
|
| Рис.3 |
| Рис. 2-4.3. Реологические кривые |
Зависимость между объемом  жидкости (или газа), протекающей в единицу времени через сечение трубы, и разностью давлений
жидкости (или газа), протекающей в единицу времени через сечение трубы, и разностью давлений 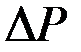 на концах трубы устанавливается известной формулой Пуазейля:
на концах трубы устанавливается известной формулой Пуазейля:
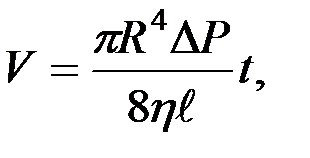 (2-4.10)
(2-4.10)
где 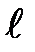 - длина трубы,
- длина трубы, 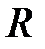 - ее радиус. Пользуясь этой формулой, можно, измерив объем жидкости V, протекающей через трубу за время
- ее радиус. Пользуясь этой формулой, можно, измерив объем жидкости V, протекающей через трубу за время 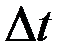 и разность давлений на ее концах, определить коэффициент вязкости жидкости.
и разность давлений на ее концах, определить коэффициент вязкости жидкости.
Рассмотрим некоторые экспериментальные методы определения коэффициента внутреннего трения жидкостей.
Метод вискозиметрии
Как уже отмечалось, коэффициент вязкости жидкости можно определить, если измерить течение газа через трубу известных геометрических размеров, пользуясь формулой Пуазейля (2-4.10). Для такого опыта необходима труба, в которой течение жидкости будет ламинарным. При определенном значении скорости в жидкости начинают появляться вихри, что вызвано появлением составляющих скорости, перпендикулярных к оси трубы (для вихревого или турбулентного течения формула Пуазейля не справедлива). Одним из методов определения измерения коэффициента вязкости, основанным на использовании формулы Пуазейля, является метод капиллярного вискозиметра.
Обоснование метода
Формулой (2-4.9) удобно пользоваться для относительного определения коэффициента вязкости. Пусть через один и тот же капилляр протекают одинаковые объемы двух различных жидкостей (  ). Тогда объемы первой и второй жидкостей, как следует из формулы Пуазейля, будут равны:
). Тогда объемы первой и второй жидкостей, как следует из формулы Пуазейля, будут равны:
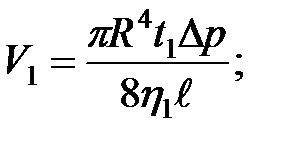 (2-4.11)
(2-4.11)
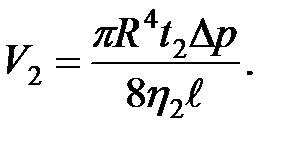 (2-4.12)
(2-4.12)
Поделив уравнение (11) на (12), получим
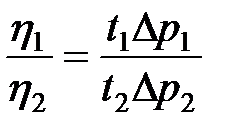 . (2-4.13)
. (2-4.13)
Если жидкость вытекает под действием силы тяжести, то разность давлений равна гидростатическому давлению, т. е.
 ,
, 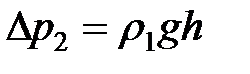 , (2-4.14)
, (2-4.14)
где 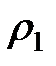 и
и 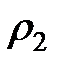 – плотность жидкости при температуре опыта. Подставляя (2-4.14) в (2-4.13), получим
– плотность жидкости при температуре опыта. Подставляя (2-4.14) в (2-4.13), получим

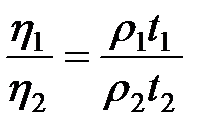 ;
; 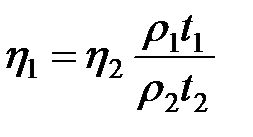 . (2-4.15)
. (2-4.15)
Приборы и принадлежности
Вискозиметр, исследуемые жидкости, секундомер.
Описание вискозиметра
| Рис. 2-4. 4. Капиллярный вискозиметр |
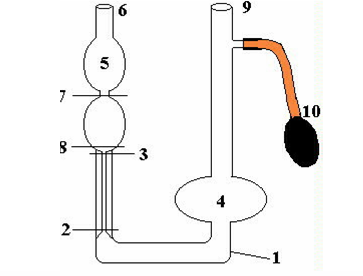 Капиллярный вискозиметр (рис. 2-4.4) представляет собой U- образную трубку 1, укрепленную вертикально. Участок трубы 2-3 выполнен в виде узкого канала; правое колено содержит шарообразное расширение 4; левое колено содержит двойное расширение 5, переходящее в верхней части в трубку 6. Метки 7-8 около верхнего расширения ограничивают определенный объем жидкости. Жидкость наливается в колено до заполнения почти всего шарообразного расширения 4. На трубку надета груша 10, при помощи которой жидкость засасывается в резервуар 5 выше метки 7.
Капиллярный вискозиметр (рис. 2-4.4) представляет собой U- образную трубку 1, укрепленную вертикально. Участок трубы 2-3 выполнен в виде узкого канала; правое колено содержит шарообразное расширение 4; левое колено содержит двойное расширение 5, переходящее в верхней части в трубку 6. Метки 7-8 около верхнего расширения ограничивают определенный объем жидкости. Жидкость наливается в колено до заполнения почти всего шарообразного расширения 4. На трубку надета груша 10, при помощи которой жидкость засасывается в резервуар 5 выше метки 7.
Порядок выполнения работы
Вискозиметр промывают испытуемой жидкостью. Укрепить его в штативе и налить испытуемую жидкость в колено 9 до метки 8.
Осторожно с помощью резиновой груши высосать жидкость выше метки 7 в резервуар 5.
Определить время истечения жидкости 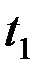 (в момент, когда мениск проходит через метку 7, включить секундомер, а при прохождении мениска через метку 8 секундомер выключить). Время истечения жидкости измеряется 5 раз. Аналогичные опыты проделать с водой. Время истечения воды
(в момент, когда мениск проходит через метку 7, включить секундомер, а при прохождении мениска через метку 8 секундомер выключить). Время истечения жидкости измеряется 5 раз. Аналогичные опыты проделать с водой. Время истечения воды 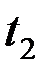 . Значения
. Значения 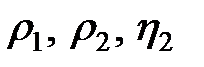 берутся из справочников. Результаты расчетов по формуле (12-4.5) и экспериментальные измерения занести в табл. 2-4.1
берутся из справочников. Результаты расчетов по формуле (12-4.5) и экспериментальные измерения занести в табл. 2-4.1
Таблица 2-4.1
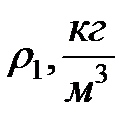
| 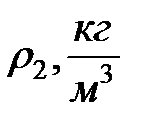
| 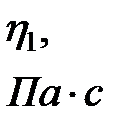
| 
| 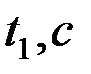
| 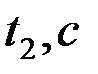
| 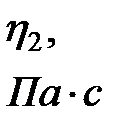
| 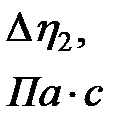
|
Обоснование метода
На твердый шарик, падающий в жидкости, действуют три силы: сила тяжести, сила Архимеда и сила трения шарика о жидкость. Эти силы равны соответственно 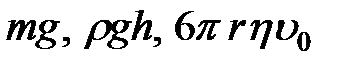 .
.
Обозначим скорость шарика относительно жидкости через 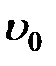 . Молекулы жидкости в слое, прилегающем к шарику, движутся со скоростью
. Молекулы жидкости в слое, прилегающем к шарику, движутся со скоростью  . Распределение жидкостей в соседних слоях, увлекаемых силами внутреннего трения, должно иметь вид, изображенный на рис. 2-4.5. В непосредственной близости от поверхности шара эта скорость равна
. Распределение жидкостей в соседних слоях, увлекаемых силами внутреннего трения, должно иметь вид, изображенный на рис. 2-4.5. В непосредственной близости от поверхности шара эта скорость равна 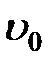 , а по мере удаления уменьшается и практически становится равной нулю на некотором расстоянии L от поверхности шарика. Очевидно, что чем больше радиус шара, тем большая масса жидкости вовлекается в движение, и L должно быть пропорционально
, а по мере удаления уменьшается и практически становится равной нулю на некотором расстоянии L от поверхности шарика. Очевидно, что чем больше радиус шара, тем большая масса жидкости вовлекается в движение, и L должно быть пропорционально 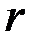 :
:
L = kr . (2-4.16)
Величина коэффициента пропорциональности несколько различна для передней и задней частей тела, поэтому под градиентом скорости следует понимать среднее значение градиента скорости на поверхности шара
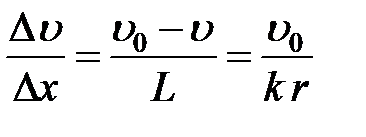 . (2-4.17)
. (2-4.17)
Полная сила трения, испытываемая движущимся шариком,
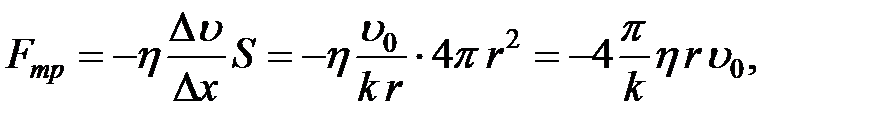 (2-4.18)
(2-4.18)
где 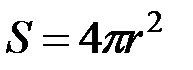 .
.
Согласно Стоксу, величина 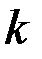 для шара равна
для шара равна 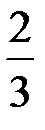 . Следовательно,
. Следовательно,
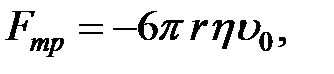 (2-4.19)
(2-4.19)
т. е. сила трения прямо пропорциональна вязкости жидкости, радиусу шара и скорости его движения. Выражение (2-4.19) носит название закона Стокса:
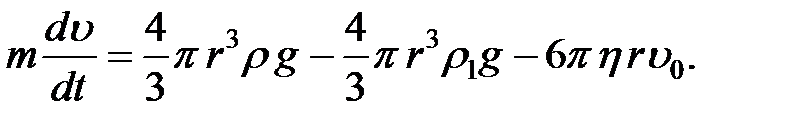 (2-4.20)
(2-4.20)

| Рис. 2-4.5. Поле сил |

| Рис. 2-4.5. Поле сил |
 (2-4.21)
(2-4.21)
Последнее выражение позволяет определить коэффициент внутреннего трения в жидкости, в которой движется шарик. Так как жидкость всегда находится в каком-то сосуде, имеющем стенки, то учет наличия стенок несколько изменит выражение для коэффициента вязкости. Для жидкости, находящейся в цилиндре с радиусом 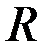 , коэффициент вязкости равен
, коэффициент вязкости равен
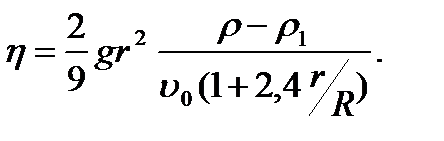 (2-4.22)
(2-4.22)
Экспериментальная часть
Приборы и принадлежности
Стеклянный цилиндр с исследуемой жидкостью плотностью  , микрометр, штангенциркуль, секундомер, шарики из материала, плотность которого
, микрометр, штангенциркуль, секундомер, шарики из материала, плотность которого 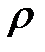 .
.
Описание прибора
Прибор состоит из стеклянного цилиндра, наполненного исследуемой жидкостью и имеющего две горизонтальные метки, расположенные на расстоянии 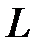 друг от друга. Верхняя метка должна быть ниже уровня жидкости на 5-8 см (рис. 2-4.
друг от друга. Верхняя метка должна быть ниже уровня жидкости на 5-8 см (рис. 2-4. 
| Рис. 2-4.6. Стеклянный цилиндр |
Порядок выполнения работы
Для определения коэффициента внутреннего трения используются шарики, диаметр которых определяется микрометром.
Желательно расположить прибор так, чтобы глаз наблюдателя находился на уровне верхней метки. При опускании шарика в жидкость необходимо учесть, что: 1) траектория его движения должна проходить как можно ближе к оси цилиндра, 2) движение шарика в жидкости должно начинаться с нулевой начальной скоростью. Прежде чем включать секундомер, необходимо выждать установления равномерной скорости движения шарика. В момент прохождения шарика мимо верхней метки включают секундомер; в момент прохождения шарика через нижнюю метку – выключают. Считая движение шарика между метками равномерным, получают скорость его движения 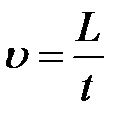 . Внутренний радиус цилиндрического сосуда
. Внутренний радиус цилиндрического сосуда 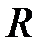 определяют штангенциркулем, опыт с разными шариками повторяют 10 раз.
определяют штангенциркулем, опыт с разными шариками повторяют 10 раз.
Измерение диаметра шариков нужно производить непосредственно перед опусканием каждого из них в жидкость, во избежание несоответствия в результатах скорости шариков их диаметрам.
Примечание. Во время опыта цилиндр с исследуемой жидкостью должен быть хорошо освещен, но лампу не следует ставить близко к сосуду во избежание нагрева исследуемой жидкости.
Результаты экспериментальных измерений и расчетов по формуле (2-4.22) занести в табл. 2-4.2:
Таблица 2-4.2
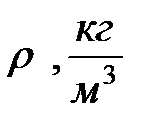
| 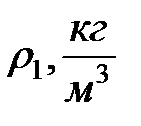
| 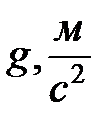
| 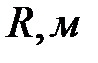
| 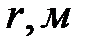
| 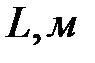
| 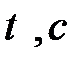
| 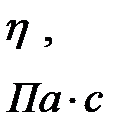
|
Оценить погрешность эксперимента.
Контрольные вопросы и задания
1. В чем заключается явление внутреннего трения в жидкости?
2. Что понимается под коэффициентами кинематической и динамической вязкости жидкостей?
3. Как изменяется коэффициент вязкости от температуры?
4. Какое движение жидкости называется ламинарным?
5. Какие силы действуют на шарик, движущийся в жидкости?
6. Какая кривая называется реологической, каков ее смысл?
7. Какие жидкости называются ньютоновскими?
8. Преобразовав путем разделения переменных и интегрированием формулу 3, проанализировать зависимость скорости слоев жидкости от координаты z.
Список рекомендуемой литературы
1. Кикоин А.К., Кикоин И.К. Молекулярная физика. М. : Наука, 1976.
2. Сивухин Д.В. Общий курс физики. Т.2. Термодинамика и молекулярная физика. М. : Наука, 1990.
3. Матвеев А.Н. Молекулярная физика. М. : Высш. шк., 1987.
4. Гинзбург В.Л., Левин Л.М., Сивухин Д.В., Яковлев И.А.. Сборник задач по общему курсу физики. Термодинамика и молекулярная физика / Под редакцией Д.В. Сивухина. М. : Наука, 1988.
5. Булкин П.С., Попова И.И. Общий физический практикум. Молекулярная физика / Под редакцией А.Н. Матвеева и Д.Ф. Киселева. М. : Изд-во Моск. Ун-т., 1988.
6. Савельев И.В. Курс общей физики. М. : Наука, 1986. Т.1.
7. Трофимова Т.И. Курс физики. М. : Высш. шк., 2001.
Лабораторная работа 2-5
Теоретическая часть
| Рис. 2-5.1. Кристаллическая решетка NaCl |
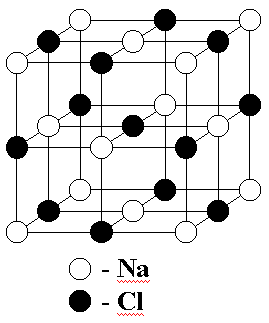
Фазовые переходы бывают двух типов - первого и второго рода. К фазовым переходам первого рода относится изменение агрегатного состояния вещества: процессы плавления и кристаллизации, испарения и конденсации, сублимации или возгонки [1], при этом скачком изменяются плотность, внутренняя энергия, энтропия.
Следует заметить, что твердым считается кристаллическое состояние, т.е. состояние, в котором атомы располагаются в узлах кристаллической решетки. На рис. 2-5.1 изображена кристаллическая решетка каменной соли NaCl . Как видно из рисунка, кристалл, благодаря пространственной периодичности структуры, состоит как бы из повторяющихся частей.
В кристалле размером 1 мм повторяющееся расположение атомов встречается сотни тысяч раз. Поэтому к такому расположению атомов применяется термин “дальний порядок”. Большинство твердых тел являются кристаллическими телами. В обычных условиях они состоят из сросшихся зерен размером порядка 0,001 мм. В таком зернышке отчетливо выражен дальний порядок.
Однако в природе встречаются твердые вещества со сложным молекулярным строением, например, стекла, смолы, пластики, которые не имеют периодической структуры. Это аморфные твердые тела, которые на самом деле являются жидкостями с аномально большой вязкостью. Такие тела приобретают свойство текучести не скачком, а путём постепенного уменьшения вязкости, которое вызывается повышением температуры. Аморфные твердые тела противопоставляются кристаллам, которые имеют форму правильного многогранника. Следует подчеркнуть, что кристалличность не обязательно проявляется в особенностях их внешней формы, это структура решетки (кусок металла не имеет правильной формы, но не является аморфным).
Каков же основной признак кристаллов? Этим признаком является наличие резко выраженной температуры плавления. Если подводить тепло к кристаллическому телу, то температура его будет повышаться до тех пор, пока не начнёт плавиться. После чего подъем температуры прекратится, и весь процесс плавления будет происходить при строго определённой постоянной температуре, называемой температурой плавления  Тпл.
Тпл.
На рис. 2-5.2 изображены схемы строения кварца и кварцевого стекла. Одно и то же в химическом отношении вещество, но одно в кристаллическом, другое в аморфном виде. Характер окружения ближайшими соседями в обоих случаях одинаков, но в аморфном теле отсутствует дальний порядок; аморфное тело – это “испорченный кристалл”. Отсутствие дальнего порядка, характерного признака кристаллических тел, является непосредственной причиной отсутствия выраженной точки плавления. В точке плавления совершается переход, при котором дальний порядок исчезает и решетка распадается на легкоподвижные субмикроскопические области, имеющие то же расположение атомов, что и исходный кристалл, но статически беспорядочно ориентированные друг относительно друга, остаётся лишь ближний порядок в расположении атомов.
Схема строения кварца
а) кристаллический, б) аморфный
(рисунок соответствует упрощенной плоской модели)
В аморфных телах при повышении температуры характер расположения атомов не меняется, увеличивается их подвижность, атомы с увеличением температуры “выскальзывают” из своего окружения, меняя соседей. Наконец число таких перемен в секунду становится таким же большим, как для жидкости.
Выше мы говорили, что при всех агрегатных превращениях поглощается или выделяется энергия. Например, для превращения килограмма воды в пар необходимо затратить энергию 2,3×106 Дж. Эта энергия необходима для преодоления сил притяжения, действующих между молекулами воды.
Металлы начинают плавиться только тогда, когда начинает разрушаться их кристаллическая решетка, на что также необходимо затрачивать энергию. Эта энергия называется скрытой теплотой плавления. Теплота плавления, отнесённая к массе вещества, называется удельной скрытой теплотой плавления. Например, для цинка она составляет 1.11×105 Дж/кг, т.е. нужно количество теплоты 111 кДж/кг, чтобы при Тпл = 419.5°С перевести 1 кг цинка из твердого состояния в жидкое. На рис. 2-5.3 представлена кривая фазового перехода твердого тела в жидкость (1). Обратное превращение – кристаллизация (2) происходит при той же температуре и сопровождается поглощением того же количества энергии, что и при плавлении – скрытой теплоты кристаллизации. Скрытой теплота перехода называется потому, что подвод (поглощение) и отвод (выделение) этой теплоты не сопровождается таким эффектом, как повышение и понижение температуры. Несмотря на то, что мы продолжаем нагревать тело (кривая правления 1), во время плавления температура не повышается, так же во время кристаллизации (кривая кристаллизации 2) температура не понижается, хотя мы продолжаем охлаждать жидкость. Переход жидкость - твердое тело сопровождается выделением энергии. Энергия взаимодействия микроскопических кристаллов становится значительно выше энергии тепловых колебаний, жидкость кристаллизуется. Однако новая фаза при таком переходе образуется не сразу во всем объеме, сначала образуются зародыши ее, которые затем растут, распространяясь на весь объем.
| 2 |
| 1 |
| t, c |
| Т, К |
| Рис. 2-5.3. Кривые плавления (1) и кристаллизации (2) твердого тела. |
К числу фазовых превращений первого рода относятся и некоторые переходы твердого тела из одной кристаллической модификации в другую. Эти превращения называются полиморфными. Кристаллы различной модификации состоят из одного и того же вещества и отличаются друг от друга лишь строением кристаллической решетки. Например, графит и алмаз состоят из одного и того же элемента – углерода. Разные структуры означают и разные физические свойства. Алмаз по физическим свойствам очень не похож на графит. Графит имеет черный цвет, он совершенно непрозрачен, алмаз же прозрачен и бесцветен; графит не горит даже при очень высоких температурах (он плавится при 385 °С), алмаз же в струе кислорода сгорает при 720 °С. Другой пример – белое и серое олово. Белое олово – блестящий, легкий и очень пластичный металл, серое олово – хрупкое и легко превращается в порошок.
Экспериментальная часть
Порядок выполнения работы
1. Вывести на минимум ручки потенциометров и тумблеры в исходное положение
2. Подать на установку питание, включив тумблер «ВКЛ» в модуле «СЕТЬ».
3. Включить тумблер «ВКЛ» в модуле «НАГРЕВ».
4. Регулятором «НАГРЕВ» модуля установить заданную мощность нагрева. Нагреть образец немного выше температуры плавления (  ). Отключить нагрев.
). Отключить нагрев.
5. Снять зависимость температуры как функции времени Т= f ( t ) в процессе охлаждения и кристаллизации образца. Показания регистрировать через 15 секунд (до 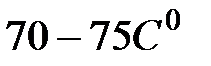 ).
).
6. Построить график зависимости Т = f ( t ). Для нахождения точек A и D на оси абсцисс влево и вправо откладывать отрезки Dt, равные времени кристаллизации металла, 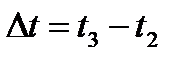 (участок ВС на кривой).
(участок ВС на кривой).
7. Оценить приращение энтропии по формуле (2), исходя из экспериментальных результатов, полученных для олова (масса образца m=0,15кг). Сделать выводы.
Контрольные вопросы и задания
1. Что называется переходом первого рода?
2. Что понимается под фазой вещества?
3. Являются ли различными фазами вещества твёрдое и жидкое стекло?
4. Чем отличаются кристаллические твёрдые тела от аморфных твёрдых тел?
5. Что происходит при плавлении твёрдых кристаллических тел и аморфных тел?
6. Что называется скрытой теплотой перехода? Почему при одних фазовых превращениях она поглощается, а при других выделяется?
7. В чём суть метода определения удельной теплоты плавления металлов?
8. Почему при кристаллизации температура остаётся постоянной, хотя мы продолжаем охлаждать металл?
9. Запишите математическое выражение второго начала термодинамики.
10. В чём заключается физический смысл понятия энтропии?
11. Как объяснить приращение энтропии при плавлении металла?
Список рекомендуемой литературы
1. Матвеев А. Н. Молекулярная физика. М.: Высш. шк., 1987.
2. Сивухин Л. В. Общая физика. Т. 2. М. – : Наука, 1993.
3. Иверонова В. И. Физический практикум. Ч. 1. М.: Высш. шк., 1968.
Лабораторная работа 2-6
Теоретическая часть
Теплоемкостью тела называется физическая величина, численно равная количеству теплоты, которое нужно подвести к телу или отнять от него для изменения его температуры на 1K. Теплоемкость, отнесенная к единице массы вещества, называется удельной теплоемкостью; теплоемкость, отнесенная к одному молю вещества, называется молярной. Обе эти величины являются характеристикой вещества, из которого состоит тело.
Из определения теплоемкости следует, что она выражается в Дж/К. Удельная теплоемкость измеряется в Дж/(кг*К), а молярная - в Дж/(моль*К). Между молярной теплоемкостью  и удельной
и удельной  существует очевидное соотношение
существует очевидное соотношение  . где
. где 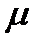 - молярная масса вещества. Если моль вещества нагревается не на 1К, а на
- молярная масса вещества. Если моль вещества нагревается не на 1К, а на 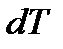 , то количество затраченной теплоты равно
, то количество затраченной теплоты равно 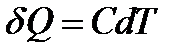 . Откуда
. Откуда
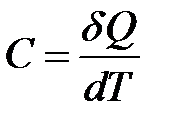 (2-6.1)
(2-6.1)
Согласно первому началу термодинамики, количество теплоты, сообщаемое термодинамической системе, идет на изменение ее внутренней энергии 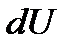 и на совершение работы
и на совершение работы  :
:
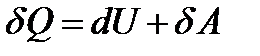 .
.
Если нагревание происходит в условиях, когда объем остается постоянным, то соответствующая теплоемкость называется теплоемкостью при постоянном объеме, или изохорической теплоемкостью, и обозначается  :
:
 .
.
Так как теплота при этом тратится лишь на изменение внутренней энергии 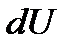 (свойство идеального газа), то
(свойство идеального газа), то
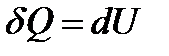 и
и  ,
,
откуда
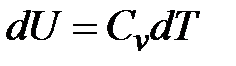 .
.
Если же при нагревании остается неизменным давление, то теплоемкость называется теплоемкостью при постояном давлении, или изобарической теплоемкостью, и обозначается  :
:
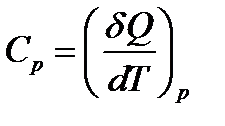 ,
,
откуда
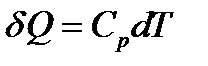 .
.
Первое начало термодинамики принимает вид:
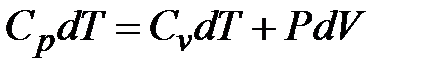 ,
,
откуда
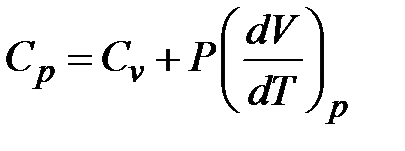 .
.
| М |

| Б |
| К |
| Н |
| Рис. 2-6.1. Схема экспериментальной установки |
| М |

| Б |
| К |
| Н |
| Рис. 2-6.1. Схема экспериментальной установки |
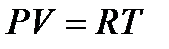 следует, что
следует, что 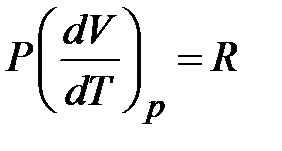 , т.е.
, т.е.  (уравнение Роберта Майера). Оно показывает, что
(уравнение Роберта Майера). Оно показывает, что 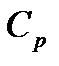 больше
больше 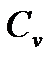 на величину универсальной газовой постоянной
на величину универсальной газовой постоянной  .
.
Величина отношения теплоемкостей газов  обозначается
обозначается 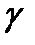 . Она зависит от сорта газа, т. е. числа степеней свободы ( i ) молекул газа. В классической теории теплоемкостей
. Она зависит от сорта газа, т. е. числа степеней свободы ( i ) молекул газа. В классической теории теплоемкостей 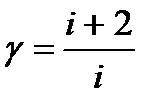 . Соответственно для одноатомных газов (
. Соответственно для одноатомных газов ( 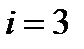 ),
), 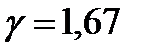 , для двухатомных (
, для двухатомных ( 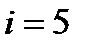 ),
), 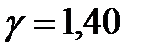 , и для трех- и многоатомных газов с нелинейными жесткими молекулами (
, и для трех- и многоатомных газов с нелинейными жесткими молекулами (  ),
), 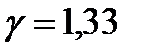 . Величина
. Величина  играет важную роль в теории теплоемкостей газов. Она входит в уравнение Пуассона (
играет важную роль в теории теплоемкостей газов. Она входит в уравнение Пуассона (  ). Зная
). Зная  , можно не прибегая к непосредственному измерению
, можно не прибегая к непосредственному измерению 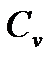 , которое порой затруднено, оценить эту величину.
, которое порой затруднено, оценить эту величину.
Существует несколько способов измерения 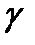 . В данной работе представлен способ оценки величины
. В данной работе представлен способ оценки величины 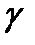 методом Клемана-Дезорма.
методом Клемана-Дезорма.
Порядок выполнения работы
Закрыть кран и накачать воздух в баллон (процесс1-2) так, чтобы величина 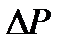 , показываемая манометром, составляла 20-25 см водного столба. Выждать не менее 2 минут, пока температуры воздуха в баллоне и окружающем пространстве не станут одинаковыми (процесс 2-3). Измерить установившееся значение величины
, показываемая манометром, составляла 20-25 см водного столба. Выждать не менее 2 минут, пока температуры воздуха в баллоне и окружающем пространстве не станут одинаковыми (процесс 2-3). Измерить установившееся значение величины 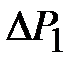 . Повернув кран, соединить баллон с атмосферой и одновременно включить секундомер. Спустя t = 55 секунд снова закрыть кран баллона (точка 6). Через некоторое время (не менее 2 минут), необходимое для выравнивания температуры газа в баллоне и окружающей среде (процесс 6-7), снова записать показание манометра
. Повернув кран, соединить баллон с атмосферой и одновременно включить секундомер. Спустя t = 55 секунд снова закрыть кран баллона (точка 6). Через некоторое время (не менее 2 минут), необходимое для выравнивания температуры газа в баллоне и окружающей среде (процесс 6-7), снова записать показание манометра 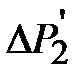 . Аналогично провести измерения для времени выдержки t =50, 40, 30, 20,15, 10 и 5 секунд. Для каждого времени выдержки опыт повторить 2 раза.
. Аналогично провести измерения для времени выдержки t =50, 40, 30, 20,15, 10 и 5 секунд. Для каждого времени выдержки опыт повторить 2 раза.
Обработка результатов
| b |
| 0 |
| 10 |
| 20 |
| t, с |
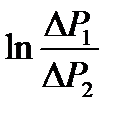
|
Рис. 3. График зависимости 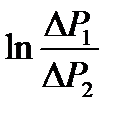 от t от t
|
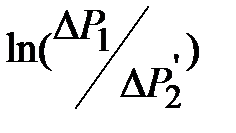 от t и экстраполировать его до пересечения с осью ординат (рис.3). Величина отрезка «b», отсекаемая на отрезке ординат позволяет найти величину
от t и экстраполировать его до пересечения с осью ординат (рис.3). Величина отрезка «b», отсекаемая на отрезке ординат позволяет найти величину 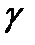 по формуле (2-6.11).
по формуле (2-6.11).
В данной работе зависимость  от t и оценка величины
от t и оценка величины 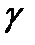 статистически обрабатывается с помощью метода наименьших квадратов, который описан в приложении (возможно выполнение этой части программы в дисплейном классе на готовой программе).
статистически обрабатывается с помощью метода наименьших квадратов, который описан в приложении (возможно выполнение этой части программы в дисплейном классе на готовой программе).
Контрольные вопросы и задания
1. Что называется теплоемкостью газа?
2. Какова размерность этой физической величины?
3. Что понимается под удельной и малярной теплоемкостями газа?
4. Как они связаны между собой? Какова связь между 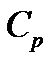 и
и  и числом степеней свободы молекул газа?
и числом степеней свободы молекул газа?
5. Получите уравнение Роберт Майера. Сколько степеней свободы имеют молекулы газов Нe, Н2, СО2?
6. Какие это степени свободы? В каком газе показатель адиабаты 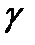 имеет наибольшее значение – N2, Нe, СН4?
имеет наибольшее значение – N2, Нe, СН4?
7. Почему в данном эксперименте целесообразно использовать сосуд возможно большего диаметра?
8. Получите уравнение адиабаты в перемененных PT и TV. Какие явления нарушают адиабатичность расширения газа?
9. Как повлияет на ход эксперимента наличие паров воды в воздухе?
Список рекомендуемой литературы
1. Матвеев А.Н. Молекулярная физика. М. : Высш. шк., 1988.
2. Булкин П.С., Попова И.И. Общий физический практикум. М. : МГУ, 1988.
3. Основы физики. Курс общей физики. Т.2. Квантовая и статистическая физика / Под. ред. Ю.М. Ципенюка. М. : Физ.-мат. лит., 2001.
Лабораторная работа № 2-7
Теплоемкость твердых тел
Теория
Теплоемкостью тела С называется отношение бесконечно малого изменения внутренней энергии этого тела dU к изменению его температуры dT:
С = 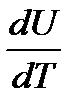 . .
| (2-7.1) |
Внутренняя энергия совпадает с энергией покоя тела (системы) и включает в себя энергию всех внутренних движений в теле и энергию взаимодействия всех частиц, составляющих это тело, включая молекулы, атомы и ионы, электроны, а также нуклоны в ядрах. Заметим сразу, что потенциальные энергии электронных оболочек атомов и ионов, потенциальные и кинетические энергии нуклонов не играют существенной роли при обычных не очень высоких температурах, когда не идут процессы ионизации и возбуждения соответствующих частиц.
Различают удельную теплоемкость – теплоемкость единицы массы вещества (одного килограмма, грамма), молярную теплоемкость – теплоемкость одного моля вещества. Единицы измерения удельной теплоемкости – Дж/кг·К (внесистемная – кал/кг·К), молярной теплоемкости – Дж/моль·К (кал/моль·К).
Различают теплоемкость при постоянном давлении Ср и теплоемкость при постоянном объеме С v. Для таких систем, как твердое тело и жидкость (в отличие от газа), изменение объема при нагревании относительно невелико и разность Ср–Сv для одноатомных твердых веществ при 100 оС составляет десятые, сотые и даже тысячные доли газовой постоянной R. Поэтому зависимостью теплоемкости от изменения объема при нагревании твердого тела обычно пренебрегают и говорят просто об удельной теплоемкости твердого тела С v, связывая ее с изменением внутренней энергии единицы массы твердого тела при нагревании на один градус.
Классическая теория теплоемкости твердых тел (кристаллов)
Простейшей моделью кристалла является правильно построенная кристаллическая решетка, в узлах которой помещаются атомы, принимаемые за материальные точки. Атомы совершают тепловые колебания около положений равновесия. Если колебания малы, то их можно считать гармоническими. Энергия каждого атома слагается из кинетической и потенциальной. На каждую степень свободы приходится в среднем кинетическая энергия ½ k Т. Из механики известно, что при гармонических колебаниях средние значения кинетической и потенциальной энергии одинаковы. Таким образом, среднее значение полной энергии, приходящейся на одну колебательную степень свободы, равно:
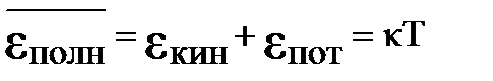 . (2-7.2)
. (2-7.2)
Рассчитаем теплоемкость кристаллической решетки на основе классических представлений. Для простоты будем считать, что все атомы одинаковы. Каждый атом обладает тремя колебательными степенями свободы, а потому на него приходится средняя энергия 3кТ. Умножив эту величину на число Авогадро Na, найдем внутреннюю энергию твердого тела:
U = 3 Na 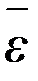 = Na 3 kT = 3 RT , (2-7.3)
= Na 3 kT = 3 RT , (2-7.3)
здесь учтено, что Na · k = R. Отсюда для молярной теплоемкости твердого тела получаем:
Cv = 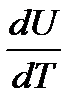 =3R ≈ 24,9
=3R ≈ 24,9 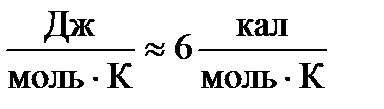 . (2-7.4)
. (2-7.4)
Этот результат находится в согласии с экспериментально установленным в 1819 г. законом (правилом) П.Дюлонга и А.Пти: молярная теплоемкость всех химически простых кристаллических твердых тел постоянна и равна 3 R (R – универсальная газовая постоянная). Мы видим, что закон Дюлонга и Пти находит простое объяснение в классической теории теплоемкости. Он сравнительно хорошо подтверждается на опыте для многих веществ при не слишком низких температурах.
Рассмотрим твердое тело, которое является химическим соединением, например, NaCl. Его кристаллическая решетка построена из атомов различных типов. Очевидно, молекулярная масса химического соединения равна сумме атомных масс всех атомов, из которых состоит молекула этого соединения. Согласно предыдущим рассуждениям, если в молекуле n атомов, то на молекулу приходится в среднем энергия 3nkT. Молярная теплоемкость будет 3nkNa = 3nR, т.е. она в n раз больше, чем у того же вещества, если бы его молекулы были одноатомными. Иными словами, молярная теплоемкость твердого соединения равна сумме молярных теплоемкостей элементарных веществ, из которых оно состоит. Это правило было найдено эмпирически и называется законом Джоуля и Коппа. Джоуль высказал его 1844 г. Но только в 1864 г. закон был окончательно сформулирован и подтвержден множеством фактов, полученных Коппом. Следует заметить, что закон Джоуля и Коппа в приведенной выше формулировке обладает большей общностью, чем закон Дюлонга и Пти. Закон Дюлонга и Пти может нарушаться, т. е. атомные теплоемкости химических элементов, входящих в соединение, могут отличаться друг от друга, но закон Джоуля и Коппа остается при этом справедливым.
Экспериментальная часть
Приборы и принадлежности
Лабораторная установка ФПТ1-8, набор образцов (алюминий, латунь, сталь).
Описание установки
Установка ФПТ1-8 представляет собой конструкцию настольного типа, состоящую из двух основных частей: 1) приборный блок; 2) блок рабочего элемента РЭ-8.
Приборный блок представляет собой единый конструктив со съемной крышкой, съемными лицевыми панелями. Внутри блока размещены печатная плата с радиоэлементами, органы подключения регулирования, трансформаторы.
На лицевой панели блока находятся цифровой контроллер для измерения времени, амперметр, вольтметр, органы управления и регулирования установки.
Блок РЭ-8 представляет собой коробчатый конструктив, укрепленный на горизонтальном основании. Несущими узлами блока РЭ-8 являются панель и кронштейн, скрепленные между собой винтами. Спереди блок закрыт съемным экраном из оргстекла. На панели расположен цифровой контроллер для измерения температуры, внизу на выступающей панели размещены образцы из различных материалов и рукоятка для установки образцов в нагреватель.
Нагреватель состоит из металлического кожуха, теплоизолирующего материала, калориметра. В калориметр вмонтирован датчик контроллера для измерения температуры.
Принцип действия установки
Удельная теплоемкость твердого тела определяется по формуле
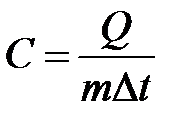 , (2-7.11)
, (2-7.11)
где C – теплоемкость, Q – количество теплоты, поглощенное образцом при нагревании на 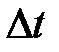 , m – масса образца,
, m – масса образца, 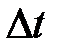 - разность конечной и начальной температур.
- разность конечной и начальной температур.
Если для нагрева пустого калориметра на 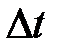 требуется Q1 джоулей тепла, а для нагрева калориметра с исследуемым образцом на
требуется Q1 джоулей тепла, а для нагрева калориметра с исследуемым образцом на 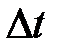 требуется Q2 джоулей тепла, то на нагрев самого образца идет
требуется Q2 джоулей тепла, то на нагрев самого образца идет
 (2-7.12)
(2-7.12)
В лабораторной установке нагрев производится пропусканием тока через нагреватель.
Количество теплоты, выделяемое нагревателем:
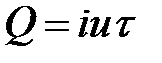 , (2-7.13)
, (2-7.13)
где i – ток через нагреватель, u – напряжение на нагревателе, t - время нагрева.
Если мощность нагрева остается постоянной в течении всего эксперимента, то после постановки выражения для количества теплоты из формулы (2-7.13) в формулу (2-7.12)
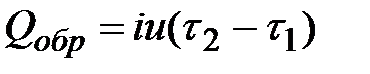 (2-7.14)
(2-7.14)
где t1 - время нагрева пустого калориметра на  , t2 - время нагрева калориметра с образцом на
, t2 - время нагрева калориметра с образцом на  .
.
Тогда 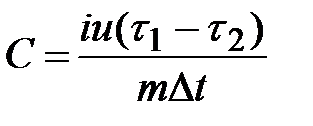 . (2-7.15)
. (2-7.15)
Порядок выполнения работы
1. Вывести на минимум ручку потенциометра в модуле «НАГРЕВ».
2. Подать на установку питание, включив тумблер «ВКЛ» в модуле «СЕТЬ».
3. Убедиться, что в калориметре отсутствует образец. Плотно закрыть крышку калориметра.
Таблица 2-7.2.
Таблица 2-7.3.
| № п.п. | Измеряемая величина | Пустой калориметр | Исследуемые образцы | ||
| латунь | алюминий | сталь | |||
| 1 |
| ||||
| 2 | m, кг | ||||
| 3 | 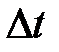 , 0С , 0С
| ||||
| 4 | t, сек | ||||
| 5 | 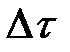 , сек , сек
| ||||
| 6 | С, 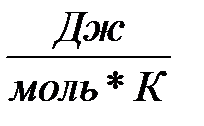
| ||||
Контрольные вопросы и задания
1. Что называется теплоемкостью тела?
2. В чем заключается суть классической теории теплоемкости твердых тел? Сформулируйте закон Дюлонга и Пти.
3. Каковы недостатки классической теории теплоемкости? Когда они проявляются?
4. Из каких положений исходит квантовая теория Эйнштейна?
5. Проанализируйте формулу теплоемкости Эйнштейна (9) при Т®¥ и Т®0.
6. Какие усовершенствования внесены в теорию теплоемкости твердых тел Дебая? Для какого интервала температур справедлив закон кубов Дебая?
7. Каково физическое содержание понятия характеристической температуры Дебая?
8. Почему при комнатной температуре теплоемкость алмаза не подчиняется закону Дюлонга и Пти?
Список рекомендуемой литературы
1. Кикоин А.К. Кикоин И.К. Молекулярная физика. М. : Наука, 1976.
2. Матвеев А. Н. Молекулярная физика. М. : Высш. шк., 1987.
3. Сивухин Д.В. Общий курс физики. Термодинамика и молекулярная физика. М. : Наука, 1993, Т. 2.
Лабораторная работа 2-8
Теплопроводность газов
Теория
Беспорядочные движения частиц газа обусловливают процессы диффузии, теплопроводности, внутреннего трения и т. д. Все эти явления имеют много общего и объединяются общим названием явления переноса. В настоящей работе изучается явление теплопроводности в воздухе.
| Рис. 2-8. 1 |
| Q |
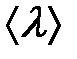
|
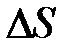
|
| Z |

Известно три способа передачи тепла: конвекция, теплопроводность, излучение. В первых двух случаях в процессе передачи тепла участвует вещество. Процесс конвекции обусловлен разностью удельных весов нагретых и холодных слоев газа. Теплопроводность - процесс переноса тепла, отличительной чертой которого является атомно-молекулярный характер передачи энергии. Сталкиваясь, молекулы передают друг другу “эстафетным способом” кинетическую энергию. Процесс теплопроводности наблюдается в системе при наличии градиента температуры.
Предположим, что в некотором объеме газа (рис. 2-8.1), в положительном направлении оси Z существует градиент температуры  . Тогда в противоположном направлении, в области более низких температур, будет наблюдаться поток тепла, который по закону Фурье пропорционален градиенту температуры:
. Тогда в противоположном направлении, в области более низких температур, будет наблюдаться поток тепла, который по закону Фурье пропорционален градиенту температуры:
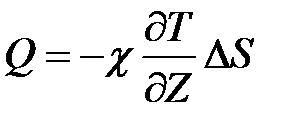 , ,
| (2-8.1) |
где  - величина площадки, через которую определяется поток тепла, c - коэффициент теплопроводности газов. Знак “минус” подчеркивает, что поток энергии и вектор градиента температуры направлены в противоположные стороны. Величина коэффициента теплопроводности согласно молекулярно-кинетической теории определяется как
- величина площадки, через которую определяется поток тепла, c - коэффициент теплопроводности газов. Знак “минус” подчеркивает, что поток энергии и вектор градиента температуры направлены в противоположные стороны. Величина коэффициента теплопроводности согласно молекулярно-кинетической теории определяется как
 , ,
| (2-8.2) |
где  - плотность газа,
- плотность газа, 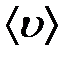 - средняя скорость теплового движения, λ - средняя длина свободного пробега,
- средняя скорость теплового движения, λ - средняя длина свободного пробега, 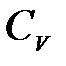 - удельная теплоемкость газа при постоянном объеме. Если в уравнении (2-8.1) градиент температуры -
- удельная теплоемкость газа при постоянном объеме. Если в уравнении (2-8.1) градиент температуры -  принять равным 1, то размерность коэффициента теплопроводности будет [вт/мК]. Из выражения (2-8.2) следует, что c не зависит от давления, так как плотность газа пропорциональна, а длина свободного пробега обратно-пропорциональна давлению газа
принять равным 1, то размерность коэффициента теплопроводности будет [вт/мК]. Из выражения (2-8.2) следует, что c не зависит от давления, так как плотность газа пропорциональна, а длина свободного пробега обратно-пропорциональна давлению газа 
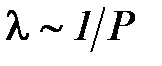 [1]. Независимость коэффициента теплопроводности от давления осуществляется не всегда. Так, для давлений, при которых длина свободного пробега молекул становится соизмерима с размерами сосуда, содержащего газ, или больше этой величины, т. е.
[1]. Независимость коэффициента теплопроводности от давления осуществляется не всегда. Так, для давлений, при которых длина свободного пробега молекул становится соизмерима с размерами сосуда, содержащего газ, или больше этой величины, т. е. 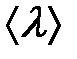 ≥ l , эта зависимость нарушается. В этом случае столкновения между молекулами самого газа перестают играть главную роль, существенными становятся только столкновения молекул со стенками сосуда, в котором заключен газ. Молекула, столкнувшись с горячей стенкой, получает от нее кинетическую энергию и переносит ее к более холодной стенке, не испытывая промежуточных столкновений. Ясно, что в таком случае перенос тепла будет происходить тем медленнее, чем меньше носителей тепла, т. е., чем больше разряжен газ. Такой перенос формально может быть описан прежней формулой 4, но величину λ следует заменить величиной l - расстоянием между стенками сосуда [2]. Процесс передачи тепла в этом случае носит название «теплопередача».
≥ l , эта зависимость нарушается. В этом случае столкновения между молекулами самого газа перестают играть главную роль, существенными становятся только столкновения молекул со стенками сосуда, в котором заключен газ. Молекула, столкнувшись с горячей стенкой, получает от нее кинетическую энергию и переносит ее к более холодной стенке, не испытывая промежуточных столкновений. Ясно, что в таком случае перенос тепла будет происходить тем медленнее, чем меньше носителей тепла, т. е., чем больше разряжен газ. Такой перенос формально может быть описан прежней формулой 4, но величину λ следует заменить величиной l - расстоянием между стенками сосуда [2]. Процесс передачи тепла в этом случае носит название «теплопередача».
Для воздуха при 200С длина свободного пробега молекул выражается эмпирической формулой [3]:
λ = 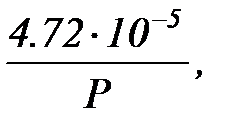
где Р- давление газа. Пользуясь этим соотношением, можно оценить то давление, при котором длина свободного пробега становится сравнима с размерами эмпирического объема.
Таким образом, независимость коэффициента теплопроводности от плотности газа имеет место лишь до тех пор, пока длина свободного пробега мала по сравнению с размерами сосуда. Когда λ и l становятся соизмеримы друг с другом, при уменьшении плотности газа коэффициент c начинает убывать. Это убывание идет по линейному закону: коэффициент c становится пропорционален плотности газа, при низком давлении теплопроводность очень мала. На этом принципе основано устройство сосудов Дюара, в которых теплоизоляция между стенками сосудов достигается с помощью вакуума.
В то же время величина c при любом давлении зависит от температуры, так как средняя скорость молекул, входящая в уравнение (2-8.2), зависит от температуры 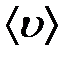
 .
.
Постановка задачи
Для изучения явления теплопроводности рассмотрим систему, состоящую из двух цилиндров с радиусами r1 и r2 (рис. 2-8.2,а). Температуры цилиндров соответственно равны Т1 и Т2 и поддерживаются с помощью внешнего источника тепла постоянными. Внутренний цилиндр может быть, в частности, просто проволокой, по которой пропускается электрический ток, и она служит нагревателем, т.е. Т1>Т2 (рис. 2-8.2,б). Поток тепла направлен от более нагретой внутренней поверхности к внешней. В случае стационарного потока распределение температур между цилиндрами будет постоянно во времени.
Используя соотношение (2-8.1), получим, что поток тепла Q в единицу времени через цилиндрическую поверхность высотой 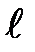 и радиусом r выражается формулой
и радиусом r выражается формулой
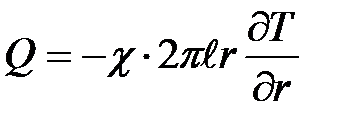 . (2-8.1)
. (2-8.1)
Интегрируя это выражение при значениях температур внутреннего и внешнего цилиндров Т1 и Т2 , получим
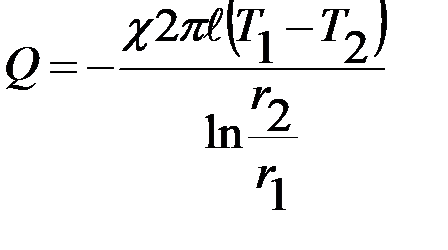 . (2-8.2)
. (2-8.2)
| r2 |
| r1 |
| r |
| а |
| r1 |
| r |
| r2 |
| б |
| Рис. 2-8.2. Система из двух цилиндров |
В стационарном состоянии поток тепла Q можно принять равным мощности нагревателя W , и тогда коэффициент теплопроводности имеет вид
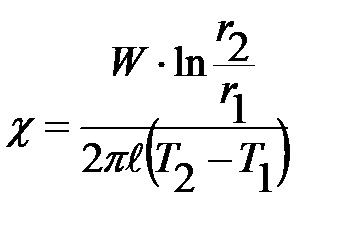
| (2-8.3) |
На практике все температуры мы определяем по шкале Цельсия, которая с абсолютной температурой связана соотношением t = ( T -273)0C. Следовательно, разность температур Т1 -Т2 в выражении (2-8.3) может быть подставлена в (2-8.3) в градусах Цельсия t 1 - t 2 (как она и определяется в эксперименте).
Таким образом, для определения величины коэффициента теплопроводности надо определить: количество тепла, переносимого от внутренней поверхности к внешней, разность температур между внутренним и внешним цилиндром, размеры системы. Все эти величины находятся из эксперимента.
Следует иметь в виду, что полученные значения будут несколько завышены, так как в процессе теплопроводности определенную роль могут играть процессы излучения и конвекции. Влияние конвекции на полученные экспериментальные результаты можно оценить, определяя коэффициент теплопроводности при разных давлениях воздуха. Известно, что с увеличением давления интенсивность конвекционного переноса тепла растет. Если в результате эксперимента обнаружится тенденция роста коэффициента теплопроводности с увеличением давления, то ее можно объяснить наличием конвективных потоков. Роль теплового излучения может быть оценена с помощью закона Стефана – Больцмана, по которому с единицы поверхности абсолютно черного тела излучается энергия W = 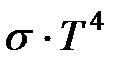 , где Т – абсолютная температура тела, а
, где Т – абсолютная температура тела, а  . Полная энергия, передаваемая при излучении от одного цилиндра к другому, не превышает
. Полная энергия, передаваемая при излучении от одного цилиндра к другому, не превышает
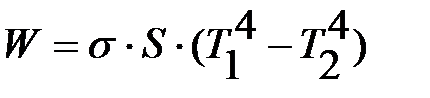 , ,
| (2-8.4) |
где S – площадь поверхности внутреннего цилиндра.
Описание установки
Для измерения коэффициента теплопроводности воздуха в данной работе используется лабораторная установка ФПТ 1-3. Установка представляет собой конструкцию настольного типа, состоящую из основных частей: 1) приборный блок, 2) рабочий элемент.
Приборный блок представляет собой единый конструктив со съемной крышкой, съемными лицевыми панелями. Внутри блока размещена печатная плата с радиоэлементами, органы подключения, регулирования, трансформаторы.
Лицевая панель блока условно разделена на три функциональных узла:
1. «НАПРЯЖЕНИЕ» осуществляет управление работой цифрового контролера для измерения напряжения.
2. «НАГРЕВ» осуществляет включение и регулирование нагрева нити.
3. «СЕТЬ» осуществляет подключение установки к сети питающего напряжения.
Рабочий элемент представляет собой коробчатый конструктив, укрепленный на стойке. Несущими узлами этого блока являются панель и кронштейн, скрепленные между собой винтами.
Между выступающими частями панели в текстолитовых фланцах зажата стеклянная трубка. По оси трубки натянута вольфрамовая нить. Между панелью и кронштейном размещен вентилятор для охлаждения трубки. На панели установлены цифровой контроллер для измерения температуры и цифровой контроллер для измерения напряжения.
В лабораторной установке тепловой поток создается путем нагрева нити постоянным током и определяется по формуле
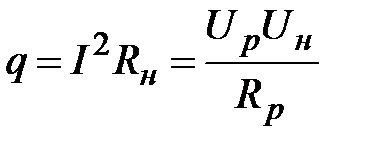 , (2-8.5)
, (2-8.5)
где 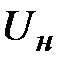 - падение напряжения на нити;
- падение напряжения на нити;
 - падение напряжения на эталонном резисторе;
- падение напряжения на эталонном резисторе;
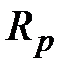 - сопротивление эталонного резистора (
- сопротивление эталонного резистора ( 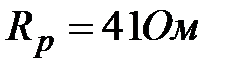 ).
).
Разность температур нити и трубки: 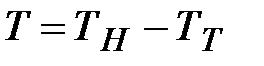 , где
, где 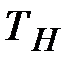 – температура нити,
– температура нити, 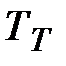 - температура трубки, равна температуре окружающего воздуха.
- температура трубки, равна температуре окружающего воздуха.
Температура трубки в процессе эксперимента принимается постоянной, т. к. ее поверхность обдувается с помощью вентилятора потоком воздуха.
Температура нити тем выше, чем больше протекающий по ней ток. С помощью температуры меняется сопротивление нити, измеряемое методом сравнения падения напряжений на нити и на эталонном резисторе.
Разность температур нити и трубки определяется по формуле
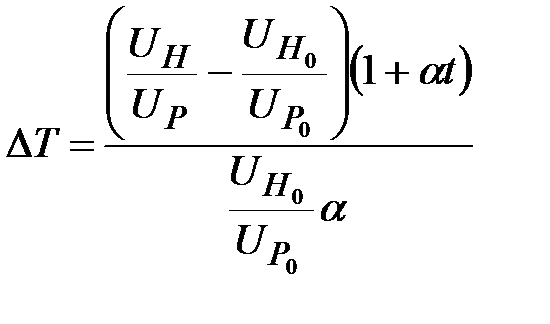 , (2-8.6)
, (2-8.6)
где 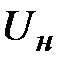 - падение напряжения на нити в нагретом состоянии;
- падение напряжения на нити в нагретом состоянии;
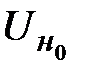 - падение напряжения на нити при температуре окружающего воздуха (при рабочем токе не более 10мА);
- падение напряжения на нити при температуре окружающего воздуха (при рабочем токе не более 10мА);
 - падение напряжения на эталонном резисторе при нагреве нити;
- падение напряжения на эталонном резисторе при нагреве нити;
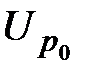 - падение напряжения на эталонном резисторе при температуре окружающего воздуха;
- падение напряжения на эталонном резисторе при температуре окружающего воздуха;
 - температурный коэффициент сопротивления
- температурный коэффициент сопротивления 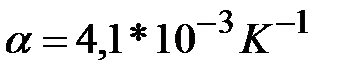 ;
;
t – температура воздуха.
Порядок выполнения работы
1. Вывести на минимум ручку потенциометра в модуле «НАГРЕВ».
2. Подать на установку питание, включив тумблер «ВКЛ» в модуле «СЕТЬ».
3. Включить тумблер «ВКЛ» в модуле «НАГРЕВ».
4. Нажать кнопку  (режим измерения падения напряжения на эталонном резисторе).
(режим измерения падения напряжения на эталонном резисторе).
5. Установить регулятором «НАГРЕВ» напряжение  не более 0,06В (негреющий ток).
не более 0,06В (негреющий ток).
6. Нажать кнопку 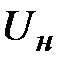 (режим измерения падения напряжения на нити) и зарегистрировать показания цифрового индикатора.
(режим измерения падения напряжения на нити) и зарегистрировать показания цифрового индикатора.
7. Рассчитать тепловой поток по формуле (2-8.5).
8. Нажать кнопку  и установить рукояткой «НАГРЕВ» напряжение в диапазоне 0,3-6,5В. Заполнить табл. 2-8.1 измерений.
и установить рукояткой «НАГРЕВ» напряжение в диапазоне 0,3-6,5В. Заполнить табл. 2-8.1 измерений.
таблица 2-8.1
 B B
|  B B
| 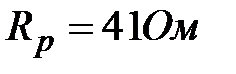
|
| |
 0C 0C
| 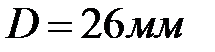
| 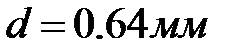
|
| |
| № п.п. |  , В , В
| 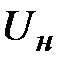 , В , В
|  , 0С , 0С
| 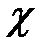
|
| 1 | 2,8 | |||
| 2 | 3,8 | |||
| 3 | 4,8 | |||
| 4 | 5,8 | |||
9. Выждать некоторое время для стабилизации теплового режима и определить падение напряжения на нити 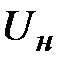 .
.
10. После измерения вывести рукоятку «НАГРЕВ» в крайнее левое положение.
11. Рассчитать разность температур по формуле (2-8.6) и определить коэффициент теплопроводности по формуле (2-8.3).
12. Рассчитать зависимость температуры проволоки от мощности нагрева W, построить ее график. Результаты занести в табл2-8.2:
таблица 2-8.2
| № п.п. |  , В , В
| 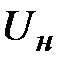 , В , В
| 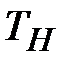 , 0С , 0С
| 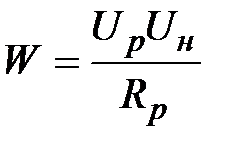
|
| 1 | 2,8 | |||
| 2 | 3,8 | |||
| 3 | 4,8 | |||
| 4 | 5,8 |
13. Оценить величину мощности излучения проволоки по закону Стефана–Больцмана.
Контрольные вопросы и задания
1. Назовите три механизма передачи тепла. В чем их физическая суть?
2. Каковы выражение и размерность коэффициента теплопроводности?
3. Как выводится размерность коэффициента теплопроводности?
4. Каков физический смысл коэффициента теплопроводности?
5. Как зависит c от давления газа и от градиента температуры газа?
6. На каком принципе устроен сосуд Дьюара?
Список литературы
1. Матвеев А. Н. Молекулярная физика М. : Высш. шк., 1987.
2. Сивухин Л. В. Общий курс физики : Термодинамика и молекулярная физика М. : Наука, 1990.
3. Булкин П.С. Общий физический практикум, Молекулярная физика М. : МГУ, 1988.
4. Бекнев В.С., Епифанов В.М., Леонтьев А.И. и др. Газовая динамика. Механика жидкости и газа / Под общ.ред. А.И. Леонтьева М.: Изд-во МГТУ им. Н.Э. Баумана, 1997.
5. Луканин В.Н., Шатров М.Г., Камфер Г.М. и др. Теплотехника / Под ред. Луканина В.Н. М. : Высш. шк., 1999.
6. Общие требования к оформлению текстовых и графических работ студентов. СТО ИрГТУ. 005-2007
Приложение 1
Приложение 2
Вывод формулы для оценки значения 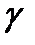
Ранее были введены обозначения 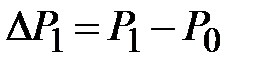 и
и  , причем
, причем 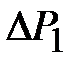 и
и 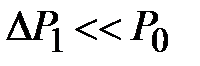 (см. рис.2). Запишем уравнение для адиабатического расширения газа (кривая 3-4)
(см. рис.2). Запишем уравнение для адиабатического расширения газа (кривая 3-4)
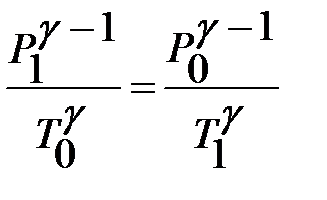 или
или 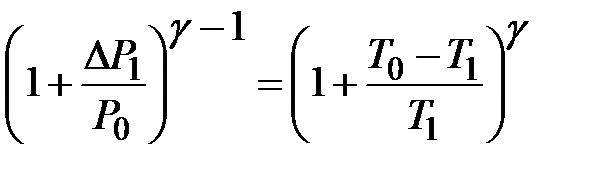 .
.
Воспользовавшись формулой бинома Ньютона и ограничиваясь двумя членами, получим
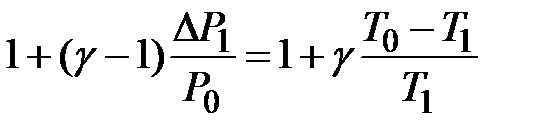 ;
; 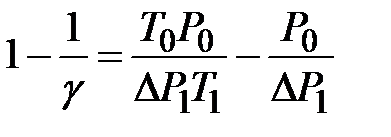 .
.
Учитывая, что 4 и 5 лежат на одной изохоре, т.е. 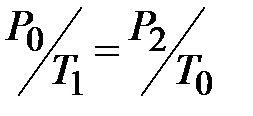 , можно записать:
, можно записать:
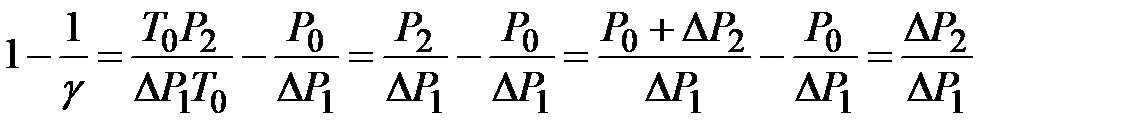 .
.
Откуда
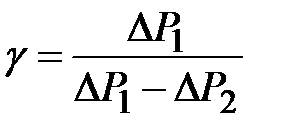 . .
|
Лабораторных работ
Издательство
Национального исследовательского
Иркутского государственного технического университета
2011
Физика. Молекулярная физика: методические рекомендации к выполнению лабораторных работ. / Сост.: А.Д. Афанасьев, Л.В. Днепровская, М.Я. Яраева Иркутск: Изд-во ИрГТУ, 2011. 92с.
Соответствует содержанию разделов государственных стандартов по направлениям 090900 Информационная безопасность, 210400 Радиотехника, 222900 Наноматериалы и микросистемная техника, 210700 Инфокоммуникационные технологии и системы связи. Содержат описания 8 лабораторных работ по курсу физики (раздел «Молекулярная физика»).
Предназначены для студентов 1 курса специальностям 090900 Информационная безопасность, 210400 Радиотехника, 222900 Наноматериалы и микросистемная техника, 210700 Инфокоммуникационные технологии и системы связи Физико-технического института Национального исследовательского Иркутского государственного технического университета
Библиогр. назв., иллюстр. 42, табл. 17
| Лабораторная работа 2-1. Изучение статистического распределения частоты электрических сигналов………………………………………... | 4 |
| Лабораторная работа 2-2. Молекулярное строение жидкостей и методы определения коэффициента поверхностного натяжения………………. | 19 |
| 2-2.1. Определение коэффициента поверхностного натяжения методом сравнения…………………………………………………………………… | 26 |
| 2-2.2. Определение коэффициента поверхностного натяжения методом компенсации разности давлений поверхностного слоя жидкости (метод Штейна)……………………………………………………………………. | 27 |
| 2-2.3. Определение коэффициента поверхностного натяжения жидкости методом отрыва кольца…………………………………………………… | 28 |
| 2-2.4. Определение коэффициента поверхностного натяжения жидкости методом отрыва капель……………………………………………………. | 30 |
| Лабораторная работа 2-3. Определение средней длины свободного пробега и эффективного диаметра молекул газа………………………… | 33 |
| Лабораторная работа 2-4. Определение коэффициента вязкости жидкости……………………………………………………………………. | 41 |
| 2-4.1. Метод вискозиметрии………………………………………………. | 47 |
| 2-4.2. Метод Стокса………………………………………………………... | 49 |
| Лабораторная работа 2-5. Изучение фазовых переходов первого рода. | 53 |
| Лабораторная работа 2-6. Определение отношения удельных теплоемкостей воздуха……………………………………………………… | 60 |
| Лабораторная работа 2-7. Теплоемкость твердых тел и ее определение методом охлаждения………………………………………………………... | 69 |
| Лабораторная работа 2-8. Теплопроводность газов…………………….. | 80 |
| Приложение 1………………………………………………………………. | 87 |
| Приложение 2……………………………………………………………...... | 88 |
Лабораторная работа 2-1
Изучение статистического распределения частоты электрических сигналов
Дата: 2019-03-05, просмотров: 712.
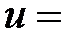 В
В 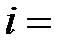 А
А