Показатель взаимосвязи Чупрова (К) предназначен для измерения

связи между количественными признаками, располагающимися в таблицах

размером S 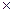t =2, где S и t – соответственно число строк и столбцов (без итогов).

Вычисление этого коэффициента основывается на измерении отклонений

наблюдаемых частот в клетках таблицы от теоретических (ожидаемых)

частот, которые задаются в предположении о независимости признаков.

Математическая логика применения показателя К базируется на

том, что, если теоретическое распределение говорит от независимости

(не связанности) признаков, то отклонение фактического от теоретического

 распределения будет тем больше, чем больше признаки взаимосвязаны.

 Это отклонение оценивается с по мощью критерия 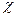, который включен

 в формулы в качестве основного элемента. Сам по себе критерий

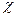² может свидетельствовать о наличии или отсутствии взаимосвязи, однако

его значение во многом зависит от числа наблюдений (n). Таким образом,

его значения не могут использоваться для сравнения корреляционных

 связей в совокупностях с разным числом наблюдений. Этот недостаток

 устраняется при использовании коэффициента Чупрова (К), имеющего формулу:

.

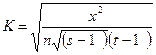Критерий Чупрова дает более точные результаты, когда таблица сопряженности

имеет квадратную форму, причем число строк и столбцов не превышает 5x5

 (без итогов). Так как расчет критерия К производится на основе 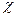² , то все

 ограничения 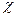² распространяются и на него.

Статистические оценки значений критерия К производятся в тех же границах,

что и обычных коэффициентов корреляции: от 0 до 1. Этим критериям, как

 правило, не приписывают никакого знака (+ или –), так как с математической точки

 зрения они являются результатом вычисления квадратного корня.

Направление связи устанавливается из содержательного смысла таблицы с

исходными данными. Если хотя бы один из признаков не может быть

 ранжирован (пол, национальность и т.п.), выяснение направления связи

вообще теряет всякий смысл.

Регрессионный анализ

Иногда при анализе корреляционных связей важно установить, как количественно

 меняется один признак по мере изменения другого на единицу.

В этих случаях регрессионный анализ осуществляется на основании вычисления

и оценки коэффициентов регрессии (R). Поскольку изменчивых величин две

 (X и Y) и регрессия является двусторонней, то соответственно будут и два

коэффициента регрессии R_xy и R_ух, которые вычисляются по формулам:

,

,

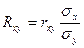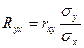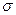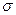где r _ху – коэффициент корреляции; _х и _у – средние квадратические

отклонения двух сравниваемых рядов.

Коэффициент регрессии характеризует только линейную зависимость и имеет

 знак «плюс» при положительной и знак «минус» - при отрицательной

связи. Между коэффициентами корреляции и регрессии имеется определенная

связь, выражающаяся формулой:

.

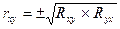Зная коэффициенты регрессии, можно легко определить коэффициенты

 корреляции.

Коэффициент регрессии нашел широкое применение в статистике физического

развития. Он показывает, например, насколько изменяется масса тела при

 увеличении роста на 1 см или возраста на 1 год. Аналогично при помощи

 коэффициента регрессии можно выяснить, как должна меняться окружность

 грудной клетки при изменении роста на 1 см.