При наличии прямолинейной связи между взаимосвязанными
количественными признаками, особенно при большом числе наблюдений,
рациональнее прибегать к параметрическим методам оценки, которые требуют
вычисления определенных параметров: средней величины (М), среднего
квадратического отклонения, средней ошибки (т). При этом вычисление
связи проводится по формуле
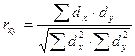 ,
,
где r ху – коэффициент линейной корреляции между двумя признаками X и Y;
d ― отклонение от средних арифметических данных ряда X и ряда Y.
Алгоритм расчета коэффициента линейной корреляции состоит из трех
основных этапов:
I этап ― определение средних арифметических Мх Му для ряда X и ряда Y;
II этап ― расчет отклонений чисел X и Y от средней арифметической этих рядов;
III этап ― определение квадратов отклонений dх2и dy2 и произведения dх dy , ,
затем производится расчет сумм этих значений: dх2и dy2 и dxdy и вычисление
по формуле Пирсона.
Коэффициент линейной корреляции Пирсона наиболее быстро
определяется по приведенной выше формуле на небольшом числе наблюдений,
которые представлены в виде простых вариационных рядов, где частоты,
как известно, равны единице. Это прямой путь вычисления коэффициента
корреляции на основе использования средних величин и отклонений от них.
Однако когда имеется большое число наблюдений и данные сгруппированы
с определенным интервалом, т.е. представлены в виде взвешенных
сгруппированных вариационных рядов, вычисление r ху производится
непрямым путем (способом) на основе метода Бравэ. Для вычисления к
оэффициента корреляции при этих условиях необходимо строить корреляционную
решетку (таблицу сопряженности). Такие условия на практике чаще
всего встречаются при изучении и оценке физического развития
отдельных групп населения. Результаты исследования в таблице
сопряженности могут быть представлены как в разном, так и в одинаковом
числе групп для подлежащего и сказуемого таблицы.
Поскольку полученные коэффициенты корреляции определяются зачастую
на материалах выборочной совокупности, всегда необходимо убеждаться в их
надежности. Репрезентативность (представительность) коэффициента может
определяться по специальным таблицам или через его ошибку
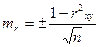 ,
,
где т – средняя ошибка коэффициента корреляции; r ху ― коэффициент
корреляции; n ― число коррелируемых пар.
Достоверным выборочный коэффициент корреляции считают только
тогда, когда его величина превышает свою среднюю ошибку в 3 раза и более.
Оценку значимости проводят и по критерию (Стьюдента). Его величину
определяют по формуле:
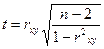 .
.
Дата: 2019-03-05, просмотров: 400.