Динамический ряд ― ряд однородных сопоставимых величин, показывающих изменение изучаемого явления во времени. Это статистическая форма отображения развития явлений во времени. Числа, составляющие динамический ряд, принято называть уровнями ряда. Уровни ряда могут быть представлены абсолютными числами, относительными и средними величинами.
Различают следующие виды динамических рядов.
Простой ― ряд, составленный из абсолютных величин, характеризующих
динамику одного явления.
Простые ряды являются исходными для построения производных рядов.
Производный ― ряд, состоящий из средних или относительных величин.
Интервальный ряд состоит из последовательного ряда чисел, характеризующих изменение явления на определенный период (по времени).
Моментный ряд состоит из величин, определяющих размеры явления не за какой-либо отрезок времени, а на определенную дату — момент.
Для более глубокого понимания сути развития общественных явлений исчисляют такие показатели динамического ряда, как абсолютный прирост, темп прироста, темп роста, абсолютное значение 1% прироста.
Абсолютным приростом называют разницу между каждым последующим уровнем и уровнем предыдущим. Абсолютный прирост может быть положительным и отрицательным.
Темпом роста называется отношение каждого последующего уровня к предыдущему, выраженному в процентах.
Темпом прироста называется отношение абсолютного прироста к предыдущему уровню, принятому за 100%.
Так как каждому относительному показателю соответствуют определенные абсолютные величины, то при изучении темпов прироста нужно обязательно учитывать, какая абсолютная величина соответствует каждому проценту прироста, каково его содержание. Для этого исчисляется такой показатель, как абсолютное значение одногопроцента прироста. Он определяется как частное от деления абсолютного прироста за определенный период на темп прироста в процентах за этот же период.
Для иллюстрации расчетов рассмотренных статистических показателей приведем ряд динамики.
Приведем пример. Необходимо дать анализ динамики рождаемости в определенном районе (таблица 5).
Т а б л и ц а 5 — Динамика рождаемости в регионе за 1996–2005гг.
| Год | Рождаемость, % | Абсолютный прирост | Темп прироста, % | Темп роста, % | Абсолютное значение 1% прироста |
| 1996 | 9,4 | — | — | — | — |
| 1997 | 8,9 | – 0,5 | – 5,3 | 94,7 | 0,09 |
| 1998 | 9,2 | 0,3 | 3,4 | 103,4 | 0,09 |
| 1999 | 9,3 | 0,1 | 1,1 | 101,1 | 0,09 |
| 2000 | 9,4 | 0,1 | 1,1 | 101,1 | 0,09 |
| 2001 | 9,2 | – 0,2 | – 2,1 | 97,9 | 0,10 |
| 2002 | 8,9 | – 0,3 | – 3,3 | 96,7 | 0,09 |
| 2003 | 9,0 | 0,1 | 1,1 | 101,1 | 0,09 |
| 2004 | 9,1 | 0,1 | 1,1 | 101,1 | 0,09 |
| 2005 | 9,2 | 0,1 | 1,1 | 101,1 | 0,09 |
Порядок вычисления следующий:
1. Определяем абсолютный прирост: 8,9 – 9,4 = – 0,5; 9,2 – 8,9 = 0,3 и т.д.
Вычисляем темп прироста: – 0,5×100/9,4 = – 5,3 и т.д.
3. Находим темп роста: 8,9×100/9,4 = 94,7 и т.д.
4. Получаем абсолютное значение 1% прироста: – 0,5/ – 5,3 = 0,09
Динамический ряд не всегда состоит из уровней, последовательно изменяющихся в сторону снижения или увеличения. Нередко уровни динамического ряда резко колеблются, и это не позволяет выявить основную тенденцию, свойственную изучаемому явлению за определённый период времени. В таких случаях проводится выравнивание динамического ряда. Существует несколько способов выравнивания динамического ряда: укрупнения интервала, сглаживание путем вычисления скользящей средней, аналитическое выравнивание по прямой и др.
Рассмотрим выравнивание по прямой линии, которое осуществляется следующим образом:
Уt (теоретические уровни) = аo+а1t, где t — условное обозначение времени, аo и а1 — параметры искомой прямой, которые находятся из решения системы уравнений:
na0 + a1Σt = Σy;
a0Σt + a1Σt2 = Σyt; где y — фактические уровни; n — число рядов динамики. Система уравнений упрощается, если t подобрать так, чтобы их сумма равнялась 0, т.е. начало отсчета времени перенести в середину рассматриваемого периода. Тогда:
a0 = Σy/n; a1 = Σyt/ Σt2.
Подставляя полученные значения a0 и a1 в формулу, вычисляют все значения теоретического уровня.
Рассмотрим следующий пример (таблица 6):
Т а б л и ц а 6: Выравнивание рождаемости за 2003–2008 г г.
| Год | Рождаемость, (у) | Условное обозначение времени, t | у×t | t×t | Теоретический уровень после выравнивания | Трехлетние скользящие средние |
| 2003 | 9,4 | – 5 | – 47 | 25 | 11 | – |
| 2004 | 8,9 | – 3 | – 26,7 | 9 | 10,1 | 9,2 |
| 2005 | 9,2 | – 1 | – 9,2 | 1 | 9,3 | 8,8 |
| 2006 | 8,3 | 1 | 8,3 | 1 | 8,5 | 8,9 |
| 2007 | 9,4 | 3 | 18,8 | 9 | 7,7 | 8,7 |
| 2008 | 8.4 | 5 | 25,2 | 25 | 6,9 | – |
n = 6 Σy = 53,6 Σyt = – 30,6 Σ t 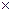 t=70.
t=70.
Если ряд четный, отсчет ведется с 1 (середина ряда), затем последовательно нечетные числа 3, 5, 7 и т.д. в обе стороны (вверх с – ; вниз с +); если ряд нечетный, отсчет условного обозначения времени ведется с 0 (середина ряда), затем — 1, 2, 3 и т.д. в обе стороны.
Порядок вычисления следующий:
Уt (теоретические уровни) = аo+а1t;
a0 = Σy/n; a1 = Σyt/ Σt2;
a0 = 8,9 a1 = – 0,4;
8,9 + (– 0,4) × (– 5) = 11;
8,9 + (– 0,4) × (– 3) = 10,1; и т.д.
Порядок вычисления скользящей средней:
Для 2004 года (9,4 + 8,9 + 9,2) / 3 = 9,2.
Для 2005 года (8,9 + 9,2 + 8,3) / 3 = 8,8 и т.д.
Укрупнение интервала производят путём суммирования данных за ряд смежных периодов (таблица 7).
Т а б л и ц а 7
| Года | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
| Рождаемость | 9,4 | 8,9 | 9,2 | 8,3 | 9,4 | 8,4 |
За 2003–2005 рождаемость составляет 9,4+8,9+9,2=27,5.
За 2006–2008 рождаемость составляет 8,3+9,4+8,4=26,1.
17. Связи между явлениями (функциональная, корреляционная). Виды корреляционной связи по силе и направлению. Метод корреляции рядов (Пирсона), этапы вычисления коэффициента корреляции, оценка достоверности
Все явления в природе и обществе находятся во взаимной связи. По характеру зависимости явлений различают:
функциональную (полную);
корреляционную (неполную) связи.
Функциональная связь означает строгую зависимость явлений, когда любому значению одного из них всегда соответствует определенное одно и тоже значение другого.
При корреляционной же связи одной и той же величине одного признака соответствуют разные величины другого. Например: между ростом и весом имеется корреляционная связь, между заболеваемостью злокачественными новообразованиямии возрастом и т.д.
По направлению различают прямые и обратные корреляционные связи. При прямой ― увеличение одного из признаков ведет к увеличению другого; при обратном же ― с увеличением одного признака второй уменьшается.
По силе связь может быть сильной, средней и слабой. На основе статистического анализа можно установить наличие связи, ее направление и измерить ее силу.
Одним из способов измерения связи между явлениями является вычисление коэффициента корреляции, который обозначается rху. Наиболее точным является метод квадратов (Пирсона), при котором коэффициент корреляции определяется по формуле: 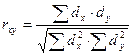 , где
, где
rху ― коэффициент корреляции между статистическим рядом X и Y.
dх ― отклонение каждого из чисел статистического ряда X от своей средней арифметической.
dу ― отклонение каждого из чисел статистического ряда Y от своей средней арифметической.
В зависимости от силы связи и ее направления коэффициент корреляции может находиться в пределах от 0 до 1 (-1). Коэффициент корреляции, равный 0, говорит о полном отсутствии связи. Чем ближе уровень коэффициента корреляции к 1 или (-1), тем соответственно больше, теснее измеряемая им прямая или обратная связь. При коэффициенте корреляции равном 1 или (-1) связь полная, функциональная.
Дата: 2019-03-05, просмотров: 348.