Все явления в природе и обществе находятся во взаимной связи. По характеру зависимости явлений различают:
функциональную (полную);
корреляционную (неполную) связи.
Функциональная связь означает строгую зависимость явлений, когда любому значению одного из них всегда соответствует определенное одно и тоже значение другого. Функциональная связь обычно выражается формулами:
(Объем тела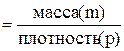 
; 
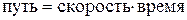и т.д.)
При корреляционной же связи одной и той же величине одного признака соответствуют разные величины другого. Например: между ростом и весом имеется корреляционная связь, между заболеваемостью злокачественными новообразованиямии возрастом и т.д.
По направлению различают прямые и обратные корреляционные связи. При прямой ― увеличение одного из признаков ведет к увеличению другого; при обратном же ― с увеличением одного признака второй уменьшается.
По силе связь может быть сильной, средней и слабой.
На основе статистического анализа можно установить наличие связи, ее направление и измерить ее силу. Одним из способов измерения связи между явлениями является вычисление коэффициента корреляции, который обозначается rху. Он может быть вычислен различными способами. Наиболее точным является метод квадратов (Пирсона), при котором коэффициент корреляции определяется по формуле:
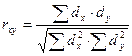, где
rху ― коэффициент корреляции между статистическим рядом X и Y.
dх ― отклонение каждого из чисел статистического ряда X от своей средней арифметической.
dу ― отклонение каждого из чисел статистического ряда Y от своей средней арифметической.
В зависимости от силы связи и ее направления коэффициент корреляции может находиться в пределах от 0 до 1 (-1). Коэффициент корреляции, равный 0, говорит о полном отсутствии связи. Чем ближе уровень коэффициента корреляции к 1 или (-1), тем соответственно больше, теснее измеряемая им прямая или обратная связь. При коэффициенте корреляции равном 1 или (-1) связь полная, функциональная.
Схема оценки силы корреляционной связи по коэффициенту корреляции
| Сила связи | Величина коэффициента корреляции при наличии | |
| прямой связи (+) | обратной связи (-) | |
| Связь отсутствует | 0 | 0 |
| Связь малая (слабая) | от 0 до +0,29 | от 0 до –0,29 |
| Связь средняя (умеренная) | от +0,3 до +0,69 | от –0,3 до –0,69 |
| Связь большая (сильная) | от +0,7 до +0,99 | от –0,7 до –0,99 |
| Связь полная (функциональная) | +1,0 | –1,0 |
Для вычисления коэффициента корреляции по методу квадратов составляется таблица из 7 колонок. Разберем процесс вычисления на примере:
Дата: 2019-03-05, просмотров: 202.
