Задачей статистического исследования является выявление закономерностей, лежащих в природе исследуемых явлений. Показатели и средние величины должны служить отображением действительности, для чего необходимо определять степень их достоверности. Правильное отображение выборочной совокупностью генеральной совокупности называется репрезентативностью. Мерой точности и достоверности выборочных статистических величин являются средние ошибки представительности (репрезентативности), которые зависят от численности выборки и степени разнообразия выборочной совокупности по исследуемому признаку.
Поэтому для определения степени достоверности результатов статистического исследования необходимо для каждой относительной и средней величины вычислить соответствующую среднюю ошибку. Средняя ошибка показателя mp вычисляется по формуле:
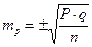
При числе наблюдений менее 30 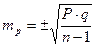 , где
, где
P — величина показателя в процентах, промилле и т.д.
q — дополнение этого показателя до 100, если он в процентах, до 1000, если %0 и т.д. (т.е. q = 100–P, 1000–P и т.д.)
Например, известно, что в районе в течение года заболело дизентерией 224 человека. Численность населения ― 33000. Показатель заболеваемости дизентерией на 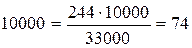
Средняя ошибка этого показателя 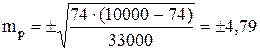
Для решения вопроса о степени достоверности показателя определяют доверительный коэффициент (t), который равен отношению показателя к его средней ошибке, т.е.
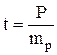
В нашем примере 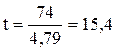
Чем выше t, тем больше степень достоверности. При t=1, вероятность достоверности показателя равна 68,3%, при t=2 ― 95,5%, при t=3 ― 99,7%. В медико-статистических исследованиях обычно используют доверительную вероятность (надежность), равную 95,5%–99,0%, а в наиболее ответственных случаях – 99,7%. Таким образом в нашем примере показатель заболеваемости достоверен.
При числе наблюдений менее 30, значение критерия определяется по таблице Стьюдента. Если полученная величина будет выше или равна табличной ― показатель достоверен. Если ниже ― не достоверен.
При необходимости сравнения двух однородных показателей достоверность их различий определяется по формуле:
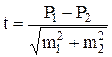 (от большего числа отнимают меньшее),
(от большего числа отнимают меньшее),
где P1–P2 ― разность двух сравниваемых показателей,
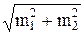 ― средняя ошибка разности двух показателей.
― средняя ошибка разности двух показателей.
Например, в районе Б в течении года заболело дизентерией 270 человек. Население района ― 45000. Отсюда заболеваемость дизентерией:
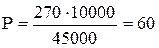
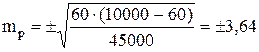
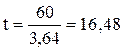 т.е. показатель заболеваемости достоверен.
т.е. показатель заболеваемости достоверен.
Как видно, заболеваемость в районе Б ниже, чем в районе А. Определяем по формуле достоверность разницы двух показателей:
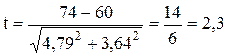
При наличии большого числа наблюдений (более 30) разность показателей является статистически достоверной, если t = 2 или больше. Таким образом, в нашем примере заболеваемость в районе А достоверно выше, т.к. доверительный коэффициент (t) больше 2.
Зная величину средней ошибки показателя, можно определить доверительные границы этого показателя в зависимости от влияния причин случайного характера. Доверительные границы определяются по формуле:
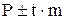 , где
, где
P ― показатель;
m ― его средняя ошибка;
t ― доверительный коэффициент выбирается в зависимости от требуемой величины надежности: t=1 соответствует надежности результата в 68,3% случаев, t=2 – 95,5%, t=2,6 – 99%, t=3 – 99,7%, t=3,3 – 99,9Величина 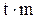 называется предельной ошибкой.
называется предельной ошибкой.
Например, в районе Б показатель заболеваемости дизентерией с точностью до 99,79% может колебаться в связи со случайными факторами в пределах 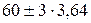 т.е. от 49,1 до 70,9 .
т.е. от 49,1 до 70,9 .
Также, как и для относительных величин необходимо для средней арифметической определять ее среднюю ошибку.
Средняя ошибка средней арифметической mx ― определяется по формуле:
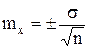 или
или 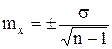 (при числе наблюдений менее 30), где
(при числе наблюдений менее 30), где
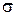 ― среднее квадратичное отклонение;
― среднее квадратичное отклонение;
n ― число наблюдений.
Определение средней ошибки средней арифметической необходимо:
1. Для оценки достоверности средней арифметической, которая определяется по формуле:
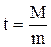
2. Для определения достоверности разности двух средних арифметических, которая определяется по формуле:
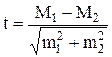
В обоих случаях оценка производится так же, как и при определении достоверности показателей, т.е. при числе наблюдений более 30 результаты достоверны, если величина доверительного коэффициента (t) равна или больше 2.
3. Для определения доверительных границ средней арифметической, т.е. в каких пределах может колебаться средняя арифметическая в зависимости от случайных факторов.
Например, обследовано 15 рабочих в цехе с высокой температурой окружающего воздуха на частоту пульса. Результаты:
| Число ударов пульса XV | Число рабочих (Р) | VP | V-M | (V-M)2 | (V-M)2P |
| 76 | 3 | 228 | -5,3 | 28,09 | 84,3 |
| 78 | 5 | 390 | -3,3 | 10,89 | 55,0 |
| 82 | 3 | 246 | 0,7 | 0,49 | 1,5 |
| 88 | 2 | 176 | 6,7 | 44,89 | 90,0 |
| 90 | 2 | 180 | 8,7 | 75,69 | 151,4 |
15 1220 382,2
Определить среднюю частоту пульса и ее достоверность.
Вначале по формуле определяем среднюю арифметическую
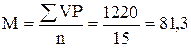 уд. в мин.
уд. в мин.
По формуле определяем среднее квадратичное отклонение
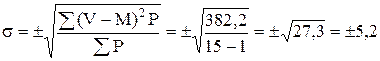
Затем по формуле вычисляем среднюю ошибку средней арифметической
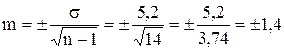
Для оценки степени достоверности средней арифметической полученные данные подставляем в формулу
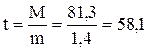
Величина достоверна.
Допустим известно, что в цехе с нормальной температурой окружающего воздуха (18―200) при обследовании 25 рабочих установлена средняя частота пульса 72,4 уд. в мин. Среднее квадратичное отклонение ― 4,8 уд. в мин, средняя ошибка 0,96. Требуется определить достоверность разности в частоте пульса у рабочих обоих цехов. Для этого данные подставляем в формулу
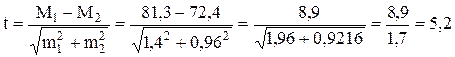
Разница в частоте ударов пульса у рабочих сравниваемых цехов статистически достоверна.
Наконец, определяем доверительные границы частоты пульса у рабочих в цехе с высокой температурой окружающего воздуха со степенью вероятности 99,7 %. 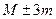 т.е. от 77,1 до 85,5 уд. в мин.
т.е. от 77,1 до 85,5 уд. в мин.
Дата: 2019-03-05, просмотров: 314.