С помощью криволинейных интегралов вычисляются
- Масса кривой;
- Центр масс и моменты инерции кривой;
- Работа при перемещении тела в силовом поле;
- Магнитное поле вокруг проводника с током (Закон Ампера);
- Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея).
Рассмотрим эти приложения более подробно с примерами.
Масса кривой
Предположим, что кусок проволоки описывается некоторой пространственной кривой C. Пусть масса распределена вдоль этой кривой с плотностью ρ (x,y,z). Тогда общая масса кривой выражается через криволинейный интеграл первого рода
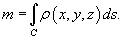
Если кривая C задана в параметрическом виде с помощью векторной функции 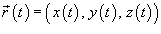 , то ее масса описывается формулой
, то ее масса описывается формулой
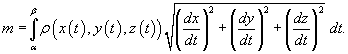
В случае плоской кривой, заданной в плоскости Oxy, масса определяется как
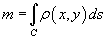
или в параметрической форме
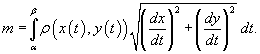
Центр масс и моменты инерции кривой
Пусть снова кусок проволоки описывается некоторой кривой C, а распределение массы вдоль кривой задано непрерывной функцией плотности ρ (x,y,z). Тогда координаты центра масс кривой определяются формулами
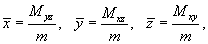
где
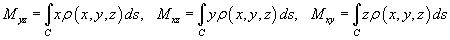
− так называемые моменты первого порядка.
Моменты инерции относительно осей Ox, Oy и Oz определяются формулами
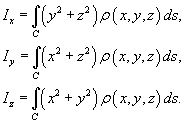
Работа поля
Работа при перемещении тела в силовом поле 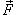 вдоль кривой C выражается через криволинейный интеграл второго рода
вдоль кривой C выражается через криволинейный интеграл второго рода
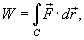
где 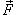 − сила, действующая на тело,
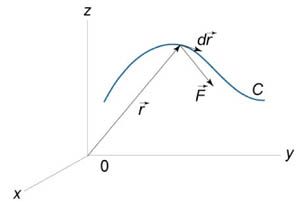
− сила, действующая на тело, 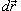 − единичный касательный вектор (рисунок 1). Обозначение
− единичный касательный вектор (рисунок 1). Обозначение 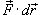 означает скалярное произведение векторов
означает скалярное произведение векторов 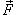 и
и 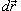 .
.
Заметим, что силовое поле 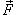 не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы
не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы 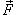 иногда может оказаться отрицательной.
иногда может оказаться отрицательной.
Если векторное поля задано в координатной форме в виде
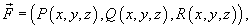
то работа поля вычисляется по формуле
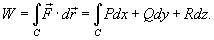
В частном случае, когда тело двигается вдоль плоской кривой C в плоскости Oxy, справедлива формула
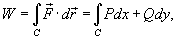
Где 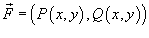
Если траектория движения C определена через параметр t (t часто означает время), то формула для вычисления работы принимает вид
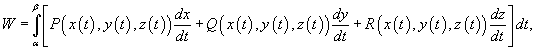
где t изменяется в интервале от α до β. Если векторное поле 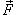 потенциально, то работа по перемещению тела из точки A в точку B выражается формулой
потенциально, то работа по перемещению тела из точки A в точку B выражается формулой
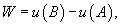 где
где 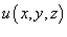 − потенциал поля.
− потенциал поля.
| 
| |
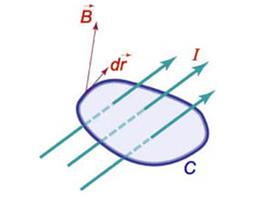
| Рис.1 | Рис.2 |
Закон Ампера
Криволинейный интеграл от магнитного поля с индукцией 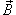 вдоль замкнутого контура C пропорционален полному току, протекающему через область, ограниченную контуром C (рисунок 2). Это выражается формулой
вдоль замкнутого контура C пропорционален полному току, протекающему через область, ограниченную контуром C (рисунок 2). Это выражается формулой
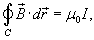
где 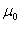 - магнитная проницаемость ваккуума, равная
- магнитная проницаемость ваккуума, равная 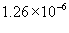 Н/м.
Н/м.
Закон Фарадея
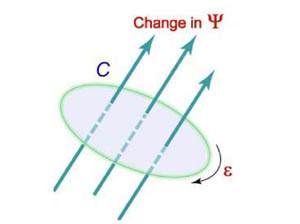
Электродвижущая сила ε, наведенная в замкнутом контуре C, равна скорости изменения магнитного потока ψ, проходящего через данный контур (рисунок 3).
|
| Рис.3 |
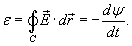
Пример
Определить массу проволоки, имеющей форму отрезка от точки A(1,1) до B(2,4). Масса распределена вдоль отрезка с плотностью 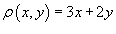 .
.
Решение. Составим сначала параметрическое уравнение прямой AB. 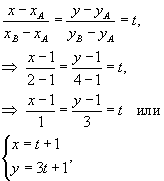
где параметр t изменяется в интервале [0,1]. Тогда масса проволоки равна
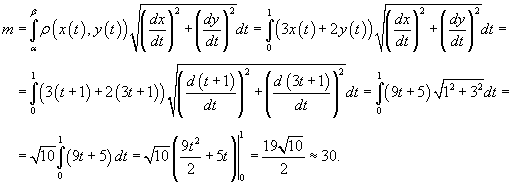
Формула грина
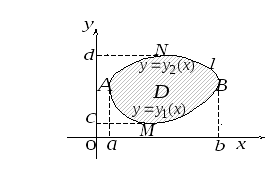
Формула Грина устанавливает связь между двойным интегралом по области 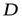 и криволинейным интегралом по контуру
и криволинейным интегралом по контуру 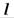 , ограничивающему эту область. Будем считать, что область
, ограничивающему эту область. Будем считать, что область 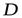 является стандартной в направлении каждой координатной оси и снизу ограничена графиком функции
является стандартной в направлении каждой координатной оси и снизу ограничена графиком функции 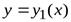 (дугой
(дугой 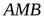 ), сверху — графиком функции
), сверху — графиком функции 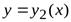 (дугой
(дугой 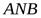 ), которые вместе составляют замкнутый контур
), которые вместе составляют замкнутый контур 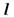 .
.
Пусть в области 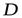 и на ее границе
и на ее границе 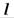 заданы функции
заданы функции 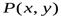 и
и 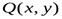 непрерывные вместе со своими частными производными
непрерывные вместе со своими частными производными 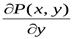 ,
, 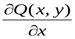 ,тогда
,тогда
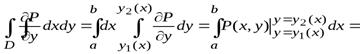
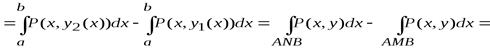
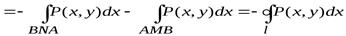 ,
,
где обход контура 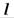 совершается в положительном направлении, т. е. против часовой стрелки (область
совершается в положительном направлении, т. е. против часовой стрелки (область 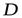 остается слева). Следовательно,
остается слева). Следовательно,
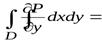
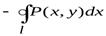 . (1)
. (1)
Аналогично получаем
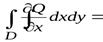
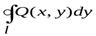 , (2)
, (2)
где обход контура 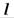 также совершается в положительном направлении.
также совершается в положительном направлении.
Вычитая почленно (1) из (2), получаем формулу Грина
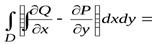
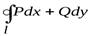 .
.
Замечание 1.Если обход контура 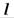 совершается в отрицательном направлении, т. е. по часовой стрелке (область
совершается в отрицательном направлении, т. е. по часовой стрелке (область 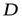 остается справа), то формула Грина принимает вид
остается справа), то формула Грина принимает вид
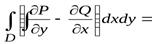
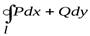 .
.
Замечание 2.Формула Грина дает возможность вычислять площадь области с помощью криволинейного интеграла. Действительно, если 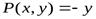 ,
, 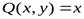 , то формула Грина перепишется так:
, то формула Грина перепишется так:
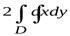
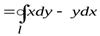 ,
,
откуда
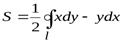 , (3)
, (3)
где обход контура 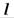 совершается против часовой стрелки.
совершается против часовой стрелки.
Пример. Определить с помощью криволинейного интеграла площадь, ограниченную эллипсом с полуосями 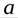 и
и 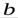 .
.
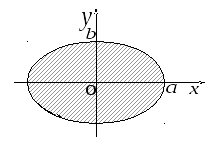
Решение.Запишем параметрические уравнения эллипса
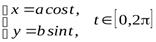 .
.
Тогда
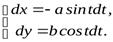
И по формуле (3) получим
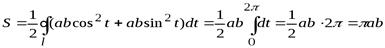 .
.
Дата: 2019-03-05, просмотров: 353.