Исходя из изложенного о пределе интегральных сумм, криволинейный интеграл второго рода записывается так:
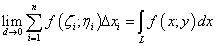 .
.
В случае криволинейного интеграла второго рода при перемене местами начала и конца отрезка кривой знак интеграла меняется:
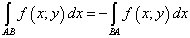 .
.
При составлении интегральной суммы криволинейного интеграла второго рода значения функции fi(ζi; ηi) можно умножать также на проекции частей отрезка кривой на ось Oy. Тогда получим интеграл
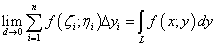 .
.
На практике обычно используется объединение криволинейных интегралов второго рода, то есть две функции f = P(x, y) и f = Q(x, y) и интегралы
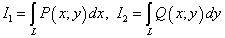 ,
,
а сумма этих интегралов
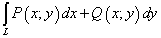
называется общим криволинейным интегралом второго рода
Геометрические и физические приложения криволинейных интегралов
Криволинейные интегралы имеют многочисленные приложения в математике, физике и прикладных расчетах. В частности, с их помощью вычисляются
- Длина кривой;
- Площадь области, ограниченной замкнутой кривой;
- Объем тела, образованного вращением замкнутой кривой относительно некоторой оси.
Длина кривой
Пусть C является гладкой, кусочно-непрерывной кривой, которая описывается вектором 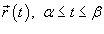 . Длина данной кривой выражается следующим криволинейным интегралом
. Длина данной кривой выражается следующим криволинейным интегралом
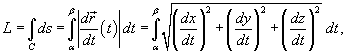
где 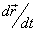 − производная, а
− производная, а 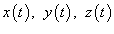 − компоненты векторной функции
− компоненты векторной функции 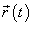 .
.
Если кривая C задана в плоскости, то ее длина выражается формулой
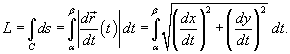
Если кривая C представляет собой график заданной явно, непрерывной и дифференцируемой функции 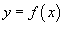 в плоскости Oxy, то длина такой кривой вычисляется по формуле
в плоскости Oxy, то длина такой кривой вычисляется по формуле
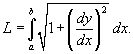
Наконец, если кривая C задана в полярных координатах уравнением 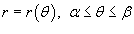 , и функция
, и функция 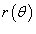 является непрерывной и дифференцируемой в интервале
является непрерывной и дифференцируемой в интервале 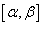 , то длина кривой определяется выражением
, то длина кривой определяется выражением
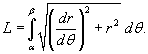
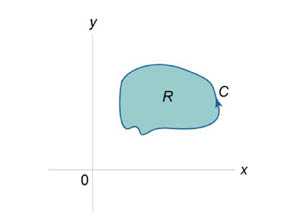
Площадь области, ограниченной замкнутой кривой
Пусть C является гладкой, кусочно-непрерывной и замкнутой кривой, заданной в плоскости Oxy (рисунок 1). Тогда площадь области R, ограниченной данной кривой, определяется формулами
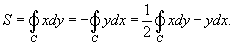
Здесь предполагается, что обход кривой C производится против часовой стрелки.
Если замкнутая кривая C задана в параметрическом виде 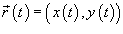 , то площадь соответствующей области равна
, то площадь соответствующей области равна
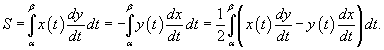
| 
| |
| Рис.1 | Рис.2 |
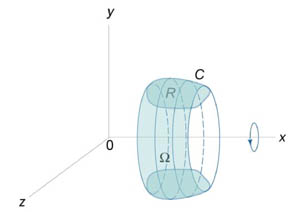
Объем тела, образованного вращением замкнутой кривой относительно оси Ox
Предположим, что область R расположена в верхней полуплоскости y ≥ 0 и ограничена гладкой, кусочно-непрерывной и замкнутой кривой C, обход которой осуществляется против часовой стрелки. В результате вращения области R вокруг оси Ox образуется тело Ω (рисунок 2). Объем данного тела определяется формулами
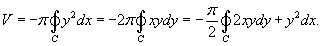
Дата: 2019-03-05, просмотров: 301.