Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).
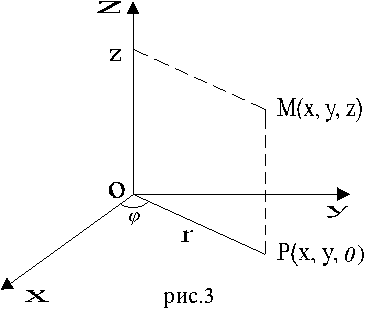
Пусть M(x, y, z) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно определяется тройкой чисел 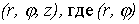 - полярные координаты точки P, z - аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид
- полярные координаты точки P, z - аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид
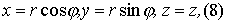
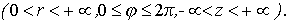
Якобиан отображения (8) 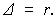
2. Сферические координаты. Пусть M(x, y) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно задаётся тройкой чисел 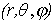 , где r - расстояние точки M до точки 0,
, где r - расстояние точки M до точки 0, 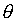 - угол между лучами OM и OZ,
- угол между лучами OM и OZ, 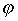 - полярный угол точки P на плоскости xy. Тройка чисел
- полярный угол точки P на плоскости xy. Тройка чисел 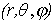 называется сферическими координатами точки M.
называется сферическими координатами точки M.
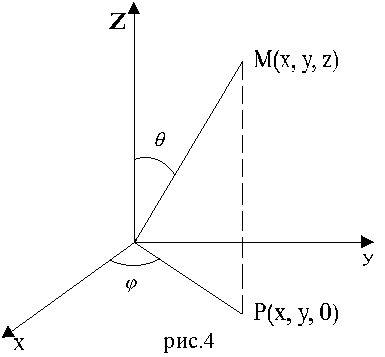
Они связаны с прямоугольными формулами
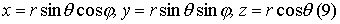
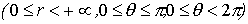
Якобиан отображения 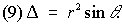 . Иногда используются обобщённые сферические координаты.
. Иногда используются обобщённые сферические координаты.
Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой
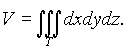
Переходя в этом равенстве к новым переменным по формулам (6), получим выражение объёма области T в криволинейных координатах
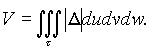
Пусть T - материальное тело (кубируемая область) с плотностью 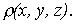
Тогда
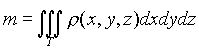 - масса тела.
- масса тела.
Тройным интегралом от функции f(x, y, z) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей):
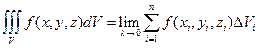 Тройной интеграл
здесь n – это количество элементарных частей разбиения области V; Pi (xi,yi,zi) – произвольно выбранная точка на каждой элементарной части,
i = 1,...,n; Тройной интеграл
здесь n – это количество элементарных частей разбиения области V; Pi (xi,yi,zi) – произвольно выбранная точка на каждой элементарной части,
i = 1,...,n;
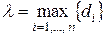 — ранг разбиения; — ранг разбиения; 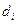 – диаметр i-ой элементарной части. – диаметр i-ой элементарной части.
|
Достаточное условие существования тройного интеграла (Сформулируйте достаточное условие существования тройного интеграла)
Если функция f (x,y,z) непрерывная в замкнутой области V, то 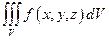 существует.
существует.
Механическая трактовка тройного интеграла (В чем состоит механическая трактовка тройного интеграла)
Если f (x,y,z) ³ 0 — это объемная плотность распределения вещества в области V, то 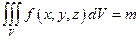 — это масса всего вещества в трехмерной области V.
— это масса всего вещества в трехмерной области V.
Приложения 2 го интеграла к решению геометр и физ. Задач.
Геометрические приложения двойных интегралов
Площадь плоской фигуры
Если f (x,y) = 1 в интеграле 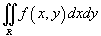 , то двойной интеграл равен площади области интегрирования R.
, то двойной интеграл равен площади области интегрирования R.
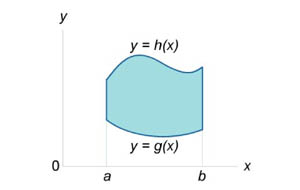
Площадь области типа I (элементарной относительно оси Оy) (рисунок 1) выражается через повторный интеграл в виде
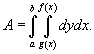
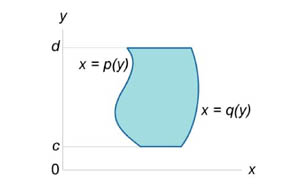
Аналогично, площадь области типа II (элементарной относительно оси Оx) (рисунок 2) описывается формулой
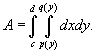
| 
| |
| Рис.1 | Рис.2 |
Объем тела
Если f (x,y) > 0 в области интегрирования R, то объем цилиндрического тела с основанием R, ограниченного сверху поверхностью z = f (x,y), выражается формулой
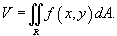
В случае, когда R является областью типа I, ограниченной линиями 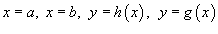 , объем тела равен
, объем тела равен
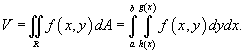
Для области R типа II, ограниченной графиками функций 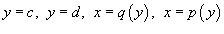 , объем соответственно равен
, объем соответственно равен
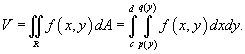
Если в области R выполняется неравенство 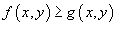 , то объем цилиндрического тела между поверхностями z1 = f (x,y) и z2 = g (x,y) с основанием R равен
, то объем цилиндрического тела между поверхностями z1 = f (x,y) и z2 = g (x,y) с основанием R равен
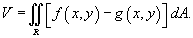
Площадь поверхности
Предположим, что поверхность задана функцией z = f (x,y), имеющей область определения R. Тогда площадь такой поверхности над областью z определяется формулой
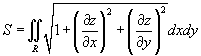
при условии, что частные производные 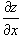 и
и 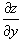 непрерывны всюду в области R.
непрерывны всюду в области R.
Дата: 2019-03-05, просмотров: 361.