Криволинейные интегралы - обобщение понятия определённого интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащий в плоскости. Общая запись криволинейного интеграла следующая:

где f(x, y) - функция двух переменных, а L - кривая, по отрезку AB которой происходит интегрирование. Если подынтегральная функция равна единице, то криволинейный интеграл равен длине дуги AB.
Как всегда в интегральном исчислении, криволинейный интеграл понимается как предел интегральных сумм каких-то очень маленьких частей чего-то очень большого. Что же суммируется в случае криволинейных интегралов?
Пусть на плоскости расположен отрезок AB некоторой кривой L, а функция двух переменных f(x, y) определена в точках кривой L. Пусть мы выполняем с этим отрезком кривой следующий алгоритм.
- Разделить кривую AB на части точками (рисунки ниже).
- В каждой части свободно выбрать точку M.
- Найти значение функции в выбранных точках.
- Значения функции умножить на
- длины частей в случае криволинейного интеграла первого рода;
- проекции частей на ось координат в случае криволинейного интеграла второго рода.
- Найти сумму всех произведений.
- Найти предел найденной интегральной суммы при условии, что длина самой длинной части кривой стремится к нулю.
Если упомянутый предел существует, то этот предел интегральной суммы и называется криволинейным интегралом от функции f(x, y) по кривой AB.
Случай криволинейного интеграла
первого рода
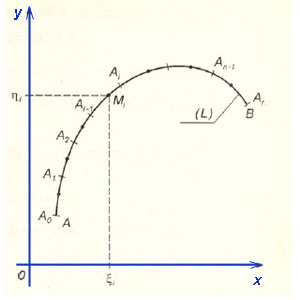
Случай криволинейного интеграла
второго рода
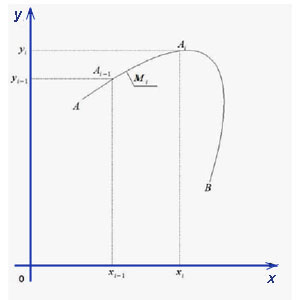
Введём следующие ообозначения.
Mi(ζi; ηi) - выбранная на каждом участке точка с координатами.
fi(ζi; ηi) - значение функции f(x, y) в выбранной точке.
Δsi - длина части отрезка кривой (в случае криволинейного интеграла первого рода).
Δxi - проекция части отрезка кривой на ось Ox (в случае криволинейного интеграла второго рода).
d = maxΔsi - длина самой длинной части отрезка кривой.
Криволинейные интегралы первого рода
Исходя из вышеизложенного о пределе интегральных сумм, криволинейный интеграл первого рода записывается так:
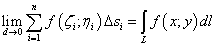 .
.
Криволинейный интеграл первого рода обладает всеми свойствами, которыми обладает определённый интеграл. Однако есть одно важное различие. У определённого интеграла при перемене местами пределов интегрирования знак меняется на противоположный:
 .
.
В случае же криволинейного интеграла первого рода не имеет значения, какую из точек кривой AB (A или B) считать началом отрезка, а какую концом, то есть
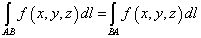 .
.
Дата: 2019-03-05, просмотров: 353.