Понятие производной по направлению
Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению
1) функции одной переменной;
2) функции трёх переменных в нашем случае.
Рассматривая функцию одной переменной, мы выяснили, что на оси Oyотображается приращение функции f(x), соответствующее приращению аргумента x. Если мы имеем дело с функцией трёх переменных, то приращения аргументов x, y, zотображаются на осях Оx, Оy, Оz. Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?
И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.
Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, - это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).
Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:
1) функцию u = f(M), определённую в окрестности точки M с координатами x, y, z;
2) произвольный вектор l с направляющими косинусами cosα, cosβ, cosγ.
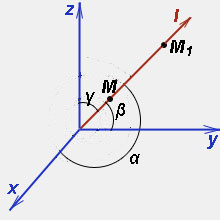
Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l. На получившейся прямой отметим точку M1, координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:
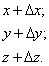
Величину отрезка MM1 можно обозначить 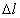 .
.
Функция u = f(M) при этом получит приращение
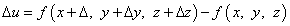 .
.
Определение производной по направлению. Предел отношения 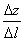 при
при 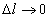 , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается
, если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается 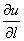 , то есть
, то есть
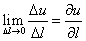 .
.
Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:
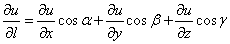 .
.
Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусыпоказывают вклад в производную по направлению соответствующей частной производной.
Примеры нахождения производной по направлению
Пример 1. Найти производную функции 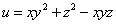 в точке M0(1; 2; 3) по направлению вектора
в точке M0(1; 2; 3) по направлению вектора 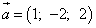 .
.
Решение. Найдём частные производные функции в точке M0:
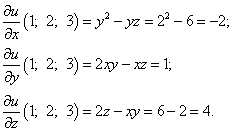
Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:
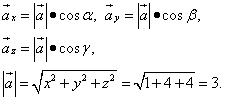
Следовательно,
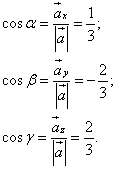
Теперь можем найти производную по направлению данной функции по её формуле:
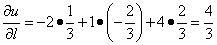
Нет времени вникать в решение? Можно заказать работу!
А сейчас - домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.
Пример 2. Найти производную функции 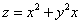 в точке M0(1; 2) по направлению вектора
в точке M0(1; 2) по направлению вектора 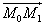 , где M1 - точка с координатами (3; 0).
, где M1 - точка с координатами (3; 0).
Посмотреть правильное решение и ответ.
Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере - в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.
Пример 3. Найти производную функции 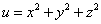 в точке M0(1; 1; 1) по направлению вектора
в точке M0(1; 1; 1) по направлению вектора 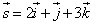 .
.
Решение. Найдём направляющие косинусы вектора
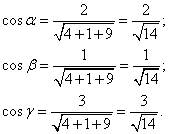
Найдём частные производные функции в точке M0:
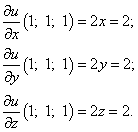
Следовательно, можем найти производную по направлению данной функции по её формуле:
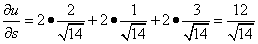 .
.
Градиент функции
Градиент функции нескольких переменных в точке M0 характеризует направление максимального роста этой функции в точке M0 и величину этого максимального роста.
Как найти градиент?
Нужно определить вектор, проекциями которого на оси координат являются значения частных производных 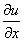 ,
, 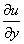 ,
, 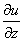 этой функции в соответствующей точке:
этой функции в соответствующей точке:
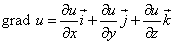 .
.
То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.
Для градиента функции двух переменных формула короче:
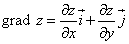 .
.
Пример 4. Найти градиент функции 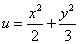 в точке M0(2; 4;).
в точке M0(2; 4;).
Решение. Найдём частные производные функции в точке M0:
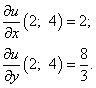
Следовательно, можем записать искомый градиент данной функции:
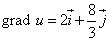 .
.
Дата: 2019-03-05, просмотров: 394.