Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности.
Для относительной характеристики величины варьирующего признака и внутреннего строения рядов распределения пользуются структурными средними, которые представлены модой и медианой.
1. Мода статистики называется такое значение варьирующего признака, который встречается в совокупности наиболее часто.
В дискретном ряду мода — это варианта с наибольшей частотой.
Пример расчета моды для дискретного ряда:
| X размер обуви | F (частота) Число пар |
| 34 | 2 |
| 35 | 10 |
| 36 | 20 |
| 37 | 88 |
| 38 | 19 |
| 39 | 9 |
| 40 | 1 |
Мода - 37
Мо — мода
Если ряд интервальный, то Мо рассчитывается по формуле
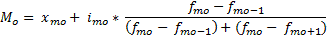
Xmo — нижняя граница модального интервала
 -величина модального интервала
-величина модального интервала
fмо- частота, соответствующая модальному интервалу
fмо-1 — частота, предшествующая модальному интервалу.
fmo+1 — частота интервала, следующая за модальным
Пример расчета моды в интервальном ряду
| d | Интервал группы | Количество предприятий |
| 1 | 330-370 | 4 |
| 2 | 371-410 | 4 |
| 3 | 411-450 | 5 – наибольшая частота |
| 4 | 451-490 | 4 |
| 5 | 491-530 | 3 |
Определяем модальный интервал 411-150
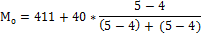
2. Медиана. Это величина, которая делит численность упорядоченного вариационного ряда на 2 равные части. 1 часть имеет значение варьирующего признака меньше средней, др.больше.
Для расчёта медианы в дискретном ряду необходимо ранжировать (упорядочить), то есть расположить все значения показателя в порядке убывания и возрастания.
Если ряд с нечётным числом индивидуальной величины, то медианой является величина или варианта, находящаяся в центре ряда.
1, 2, 2, 3, 5, 7, 10
( Ме = 3)
А если ряд с чётным числом индивидуальной величины, то медиана будет средней арифметической из двух смежных вариант, лежащих в центре ряда.
1, 2, 2, (3, 5), 7, 10, 11
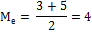
В интервальном вариационном ряду порядок нахождения следующий :
1) располагаемое индивидуальное значение признака (интервальна) групп по ранжиру
2) определяем для данного ранжированного ряда накопленные частоты
3)по данным о накопленных частотах находим медианный интервал
4)поскольку медиана делит численность ряда пополам, то следовательно, что величина её находится там, где сумма накопленных частот составляет половину или больше половины всей суммы частот.
5)Далее медиану рассчитываем по формуле:
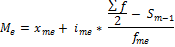
 - нижняя граница медиального ряда
- нижняя граница медиального ряда
ime- величина медианного интервала
Σf / 2 –полусумма частот ряда
S m-1 -сумма накопленных частот, предшествовавшие медианный интервал
fme- частота медианного ряда
Sm-1- сумма накопленных частот, предшествующих медиальному интервалу
Пример расчета медианы для интервального ряда
| X интервал группы | F количество предприятий |  сумма накопленных частот сумма накопленных частот
| |
| I | 330-370 | 4 | 4 |
| II | 371-410 | 4 | 8 |
| III | 411-450 5 13 Медиальный интервал | ||
| IV | 451-490 | 4 | 17 |
| V | 491-530 | 3 | 20 |

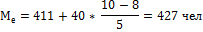
Дата: 2019-03-05, просмотров: 412.